广东省H1N1(甲流) sas 时间序列模型 拟合和预测

1、YY分析结束白噪声检验平稳性检验获得观察值序列NN差分运算拟合ARMA模型5.1.2 ARMA模型的求解与检验用sas求解的步骤与结果如下：数据的处理与模型的确认H1n1人数增加的趋势，该时间序列不平稳。原始数据一阶差分之后，方差随着时间不断地变大。但是 ，对该序列取自然对数并进行一阶差分后所的序列如图2，转换后数据比较平稳了。对序列,绘制自相关函数和偏自相关函数图(图3), Autocorrelations Lag Covariance Correlation -1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1 Std Error 0 0.307143 1.

2、00000 | |*| 0 Partial Autocorrelations Lag Correlation -1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1 1 0.00890 | . | . | 2 -0.24533 | . *| . | 3 -0.10066 | . *| . | 4 -0.00144 | . | . | 5 -0.09838 | . *| . | 6 0.09997 | . |* . | 7 -0.08299 | . *| . |白噪声检查 Autocorrelation Check for White Noise To Chi- P

3、r Lag Square DF ChiSq -Autocorrelations- 6 2.86 6 0.8264 0.009 -符合白噪声过程H1n1对数的自相关和偏相关图 Autocorrelations Lag Covariance Correlation -1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1 Std Error 0 1.658396 1.00000 | |*| 0 . marks two standard errors Partial Autocorrelations Lag Correlation -1 9 8 7 6 5 4 3 2 1

4、 0 1 2 3 4 5 6 7 8 9 1 1 0.82747 | . |* | 2 -0.13261 | . *| . | 3 -0.04033 | . *| . | 4 0.08262 | . |* . | 5 -0.11815 | . *| . | 6 0.02544 | . |* . | 7 0.00290 | . | . |从图3中可初步确定，此序列符合AR（1）。AG（1） Conditional Least Squares Estimation Standard Approx Parameter Estimate Error t Value Pr |t| Lag AR1,1 1

5、.00000 0.03037 32.92 |t| Lag MA1,1 -0.82804 0.33915 -2.44 0.0217 1 AR1,1 0.37551 0.43489 0.86 0.3958 1 AR1,2 0.62449 0.44343 1.41 0.1709 2 Number of Residuals 29 Autoregressive Factors Factor 1: 1 - 0.37551 B*(1) - 0.62449 B*(2) Moving Average Factors Factor 1: 1 + 0.82804 B*(1)结论：模型最终拟合口径 X(t)= x(t

6、-1)+ x(t-2)+e(t)+e(t-1) X(t)为序列，e(t)是随机误差从AIC BIC最小原则，多应该选择第一个模型AG(2)，但是它是不符合实际意义的，h1n1肯定会上升一段之后降下来的。所以选择第二个模型ARMA(2,1)。：模型检验利用第二步所建模型,计算残差相关系数,如果模型合适,则残差应是一随机序列。LB统计量一列概率值都大于0.05，说明所有分布临界值，于是得到结论：模型的随机误差序列是一个白噪声序列。 Autocorrelation Check of Residuals To Chi- Pr Lag Square DF ChiSq -Autocorrelations-

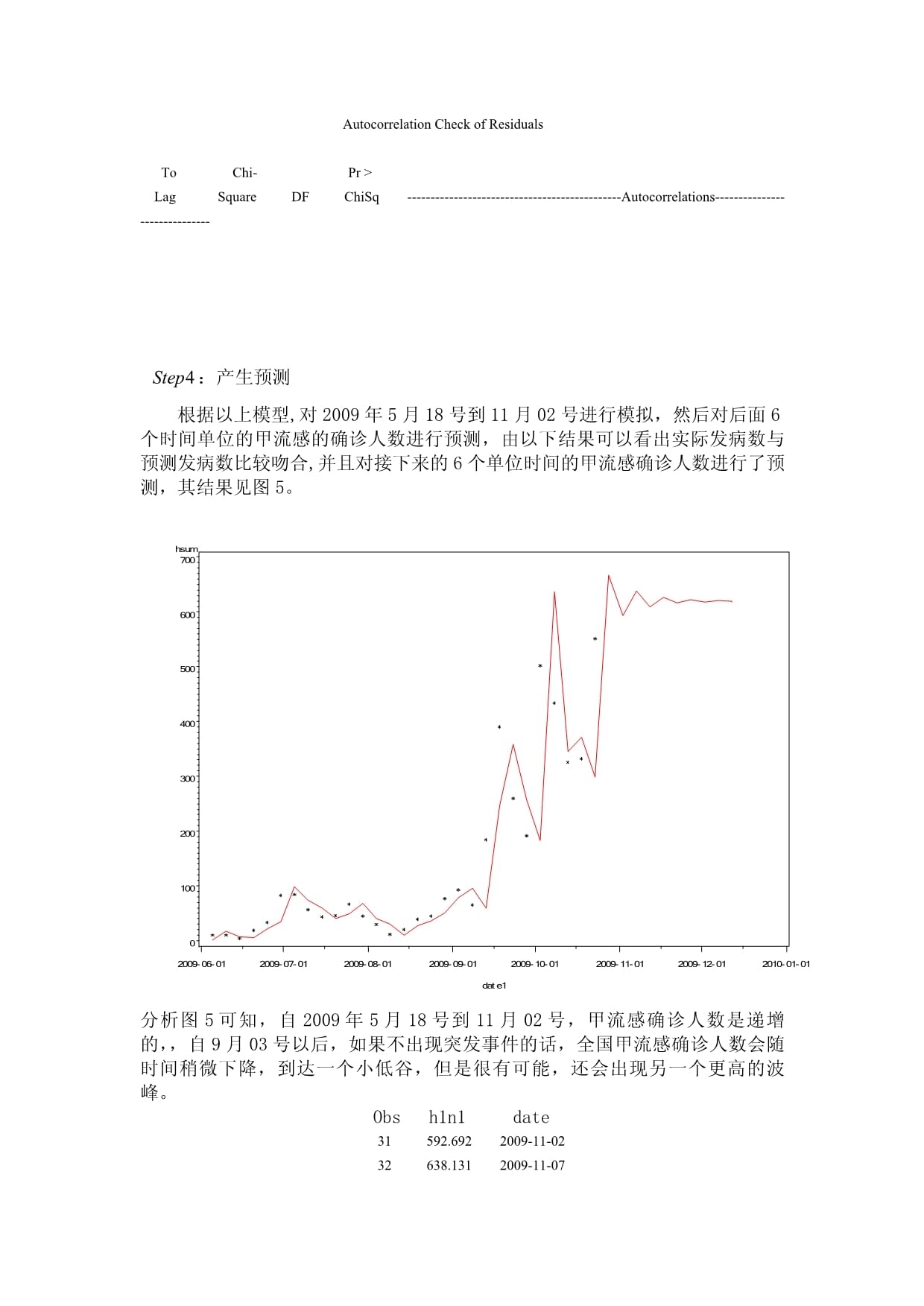
7、：产生预测根据以上模型,对2009年5月18号到11月02号进行模拟，然后对后面6个时间单位的甲流感的确诊人数进行预测，由以下结果可以看出实际发病数与预测发病数比较吻合,并且对接下来的6个单位时间的甲流感确诊人数进行了预测，其结果见图5。 分析图5可知，自2009年5月18号到11月02号，甲流感确诊人数是递增的，自9月03号以后，如果不出现突发事件的话，全国甲流感确诊人数会随时间稍微下降，到达一个小低谷，但是很有可能，还会出现另一个更高的波峰。 Obs h1n1 date 31 592.692 2009-11-02 32 638.131 2009-11-07 33 609.361 2009-

8、11-12 34 627.170 2009-11-17 35 615.987 2009-11-22 36 622.946 2009-11-27 37 618.590 2009-12-02 38 621.305 2009-12-07 39 619.607 2009-12-12：模型缺陷AR(2)不具有长期记忆功能，只能进行短期的预测，长期预测会趋于一个常数均值，明显是不适合h1n1的特点的附录：Sas程序和数据；/*数据读入和处理成最总数据机的过程*/PROC IMPORT OUT= WORK.h1n1 DATAFILE= E:h1n1.xls DBMS=EXCEL2000 REPLACE; S

9、HEET=Sheet1$; GETNAMES=YES;RUN;data b;format date yymmdd10.;set h1n1;year=year(date);year=2009;month=month(date);day=day(date);date=mdy(month,day,year);drop year month day f5 ;run;/*缺失值处理*/*累计的平摊*/data c;set b;retain q 1;if q=0 then hsum=0;hsum+h;if mod(_n_,5)=0 then q=0;else q=1;run;data g;set c;if

10、 mod(_n_,5)=0 and hsum=0 then output;run;data g;set g;t=_n_;t2=t*2;t3=t*3;run;/*处理部分*/data difvar;set g;dif=dif(hsum);/*一届差分*/r2=dif*2;/*一届差分的平方*/y=log(hsum);/*对数*/dify=dif(y);/*对数一届差分*/;proc gplot;/*原始散点图，一届差分显示方差不齐，放大一届差分的不齐，一届对数，一届对数方差齐性： */plot hsum*date dif*date r2*date y*date dify*date;symbol

11、c=black i=join v=none;proc arima;/*原始和对数的残差 白噪声检查：对数拟合 比较好*/identify var=y;/*对数*/estimate p=1 noint;/*没有常数项 (AR(2) p=1 ARMA(2,1)p=2 q=1) */forecast lead=10 id=date out=out2;data out2;format date1 yymmdd10.;merge difvar out2;by date;retain date1 31may2009d;date1+5;estimate=exp(forecast);/*对数估计值的反对数*/

12、proc gplot;/*拟合*/plot hsum*date1=1 estimate*date1=2 /overlay;symbol1 c=black i=none v=star h=;symbol2 c=red i=join v=none;run;quit;proc print data=out2;var estimate date1;run;datethsum5-191115-2810125-2911355-3012385-31133116-1141126-2151136-3164176-4170176-5185226-6191236-7200236-8211246-9220246-10

13、233276-11244316-12252336-13264376-14274416-15285466-16291476-17309566-18317636-193210736-20337806-2134311116-2235111226-2336191416-2437151566-253871636-2639211846-2740302146-2841192336-294272406-304382487-144202687-24592777-346122897-447153047-54813057-649223277-75053327-85152897-95263437-105363497-

14、115423517-125533547-135673617-1457273887-155873957-1659114067-1760164227-1861184407-1962104507-2063124627-2164154777-22657-23667-2467305077-25687-26697-2770175247-287145287-297245327-307355377-317455428-17505428-27635458-37715438-47835498-57975568-68025588-78135618-88245658-98355708-108405708-118555

15、758-128625778-138755828-1488276078-1589136208-169066268-179106268-1892146408-1993126528-2094266788-2195166948-2296267208-239777278-249827298-2599267558-26100127678-27101177848-28102198038-29103198228-3010418238-3110528259-1106128379-2107168539-3108348879-4109179049-5110729769-611129789-7112139919-81138110729-91147111439-101157112149-1111611113259-121176113869-131187714639-141193715009-151203615369-161216115979-1712212617239-181239-191249-201259-2112619219159-221279-231289-241299-251309-261319-271329-2813350224179-291349-3013510-113610-213710-313810-413910-514010-