广东省惠州市博罗县职业高级中学2022年高三数学文模拟试卷含解析

广东省惠州市博罗县职业高级中学2022年高三数学文模拟试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有是一个符合题目要求的1.已知集合，，则（

）A．

B．

C.

D．参考答案：【知识点】交集及其运算．A1

【答案解析】B

解析：由A中不等式变形得：（x+1）（x﹣2）≥0，解得：x≤﹣1或x≥2，即A=（﹣∞，﹣1]∪[2，+∞），∵B=[﹣2，2），∴A∩B=[﹣2，﹣1]．故选：B．【思路点拨】求出A中不等式的解集确定出A，再由B，求出A与B的交集即可．2.已知，是两条不同直线，，是两个不同的平面，且，，则下列叙述正确的是（A）若，则

（B）若，则（C）若，则

（D）若，则参考答案：DA中m，n可能异面；B中，可能相交；C中可能或，故选D.3.若方程在（-1，1）上有实根，则的取值范围为（

）A．

B．

C．

D．参考答案：C4.过抛物线y2=4ax（a＞0）的焦点F作斜率为﹣1的直线l，l与离心率为e的双曲线(b＞0)的两条渐近线的交点分别为B，C．若xB，xC，xF分别表示B，C，F的横坐标，且，则e=（）A．6 B． C．3 D．参考答案：D【考点】抛物线的简单性质．【分析】过抛物线y2=4ax（a＞0）的焦点F（a，0），所以直线y=﹣x+a与y=±交于B、C两点，求出B、C的横坐标，再根据且，建立关于a、b的等式解出b2=2a2，可得此双曲线的离心率．【解答】解：过抛物线y2=4ax（a＞0）的焦点F作斜率为﹣1的直线l，直线方程为y=﹣x+a，∵双曲线的渐近线为y=±x，∴直线y=﹣x+a与渐近线的交点横坐标分别为xB=，xB=，xF=a，∵，∴a2=﹣，解得2a2=b2，∴e===，故选：D5.设函数,则下列结论正确的是

A.f(x)的图像关于直线对称

B.f(x)的图像关于点对称C.把f(x)的图像向左平移个单位,得到一个偶函数的图像D.f(x)的最小正周期为,且在上为增函数参考答案：C略6.设集合Ｍ＝｛ｘ｜ｘ０Ｘ∈Ｒ｝．Ｎ＝｛x｜＜１x∈Ｒ｝。则Ｍ∩Ｎ=（）(A)

(B)

(C)

(D)

参考答案：D7.函数的图象大致是参考答案：C函数为奇函数，所以排除A.当时，，排除D.函数为奇函数，且，令得，由于函数为周期函数，而当时，，当时，，则答案应选C.8.某几何体的三视图如图所示，则此几何体的体积等于A.30 B.12 C.24 D.4参考答案：【知识点】由三视图求面积、体积．G2C

解析：由图可得几何体的直观图如右图，可得此几何体的体积等于×3×4×5-××3×4×3=24.【思路点拨】三视图复原的几何体是三棱柱去掉一个三棱锥的几何体，结合三视图的数据，求出体积即可.9.已知区域，区域，在内随机投掷一点M，则点M落在区域A内的概率是（

）A. B. C. D.参考答案：B【分析】先求出区域对应的面积，和区域对应的面积，再由几何概型，即可得出结果.【详解】由题意，对应区域为正方形区域，其面积为；对应区域如下图阴影部分所示：其面积为，所以点落在区域内的概率是.故选B【点睛】本题主要考查与面积有关的几何概型，熟记概率计算公式、以及微积分基本定理即可，属于常考题型.

10.正中，点在边上，且，则的余弦值是（

）（A）

（B）（C）

（D）参考答案：D二、填空题:本大题共7小题,每小题4分,共28分11.记直线：（）与坐标轴所围成的直角三角形的面积为，则

.参考答案：略12.过圆锥高的三等分点，作平行于底面的截面，它们把圆锥的侧面分成的三部分面积之比为_____△______．参考答案：答案：13.已知函数，若关于x的方程有且只有四个不相等的实数根，则实数k的取值范围是__ __．参考答案：（，）略14.已知函数f（x）=log2（x2﹣ax+a2）的图象关于x=2对称，则a的值为

．参考答案：4【考点】奇偶函数图象的对称性．【专题】计算题；数形结合．【分析】由题意，先研究函数的定义域，当a=0时不合题意，当a≠0时，定义域为R，故函数的对称轴即内层函数的对称轴【解答】解：由题意，a=0时不合题意当a≠0时，△=﹣3a2＜0，定义域为R，又内层函数的对称轴为x=∵函数f（x）=log2（x2﹣ax+a2）的图象关于x=2对称∴x==2∴a=4故答案为4【点评】本题考查函数图象的对称性，求解本问题的关键是由函数的解析式得出函数的对称轴即内层函数的对称轴，由此关系建立方程求出参数的值即可．15.已知总体的各个个体的值由小到大依次为2，3，3，7，a，b，12，13.3，18.7，20．且总体的中位数为10.5，则总体的平均数为．参考答案：10略16.在正项等比数列中，是的两个根，则

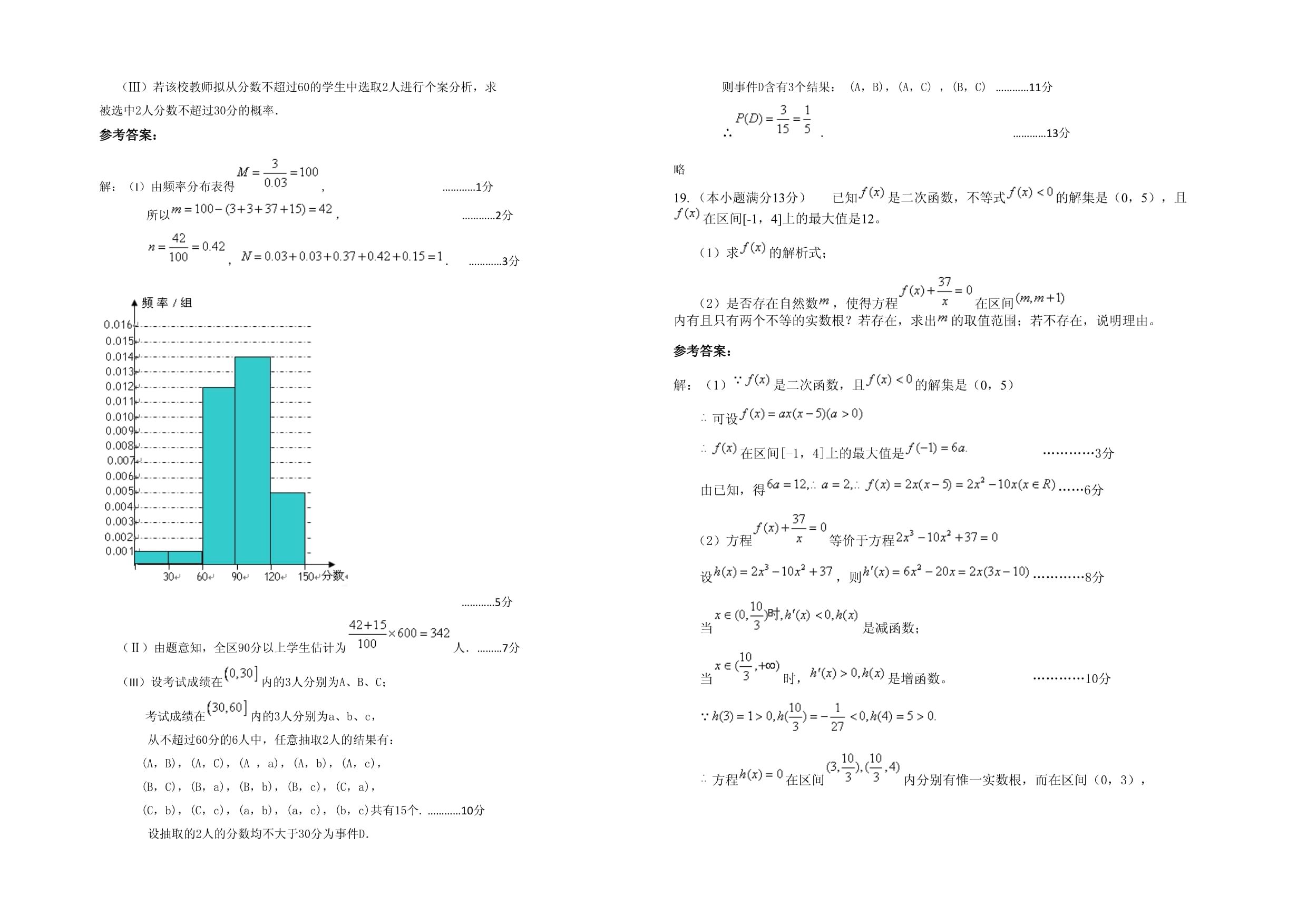
．参考答案：17.已知下列给出的四个结论:①命题“若,则方程有实数根”的逆否命题为:“若方程无实数根,则≤0”；②；③在△ABC中,“”是“”的充要条件；④设则是为偶函数”的充分而不必要条件；则其中正确命题的序号为_________________(写出所有正确命题的序号). 参考答案：【知识点】充要条件.A2【答案解析】①②④解析：解：①因为命题的逆否为，即否定条件又否定结论.所以①正确.②当时，成立.③因为时，在三角形中角A，所是“”是“”的充分条件，而不是必要条件，所以③不正确.④中当时，为偶函数，而当为偶函数时，可以为与终边相同或相反的无数个角.所以正确序号为①②④【思路点拨】根据每个小项进行分析，对充分必要关系进行计算，最后找出正确结果.三、解答题：本大题共5小题，共72分。解答应写出文字说明，证明过程或演算步骤18.我区高三期末统一测试中某校的数学成绩分组统计如下表：分组频数频率合计（Ⅰ）求出表中、、、的值，并根据表中所给数据在下面给出的

坐标系中画出频率分布直方图；

（Ⅱ）若我区参加本次考试的学生有600人，试估计这次测试中我区成绩

在分以上的人数；（Ⅲ）若该校教师拟从分数不超过60的学生中选取2人进行个案分析，求

被选中2人分数不超过30分的概率．参考答案：解：（I）由频率分布表得,

…………1分

所以，

…………2分

，．

…………3分

…………5分

（Ⅱ）由题意知，全区90分以上学生估计为人．………7分

（III）设考试成绩在内的3人分别为A、B、C；考试成绩在内的3人分别为a、b、c，

从不超过60分的6人中，任意抽取2人的结果有：

(A，B)，(A，C)，(A，a)，(A，b)，(A，c)，

(B，C)，(B，a)，(B，b)，(B，c)，(C，a)，

(C，b)，(C，c)，(a，b)，(a，c)，(b，c)共有15个.…………10分

设抽取的2人的分数均不大于30分为事件D．

则事件D含有3个结果：(A，B)，(A，C)，(B，C)

…………11分

∴．

…………13分略19.（本小题满分13分） 已知是二次函数，不等式的解集是（0，5），且在区间[-1，4]上的最大值是12。

（1）求的解析式；

（2）是否存在自然数，使得方程在区间内有且只有两个不等的实数根？若存在，求出的取值范围；若不存在，说明理由。参考答案：解：（1）是二次函数，且的解集是（0，5）

可设

在区间[-1，4]上的最大值是

…………3分

由已知，得……6分

（2）方程等价于方程

设，则…………8分

当是减函数；

当时，是增函数。

…………10分

方程在区间内分别有惟一实数根，而在区间（0，3），（4，+∞）内没有实数根，所以存在惟一的自然数，使得方程在区间内有且只有两个不等的实数根。…………13分20.（本小题满分12分）已知向量，，(1) 若,求的值；(2) 若，,求的值.参考答案：解：（1）因为，所以,

………2分于是，故

………4分（2）

由知,所以

………6分

从而

即于是

………9分

又由知，所以或因此或

………12分略21.已知函数的定义域为，对定义域内的任意，满足，当时，为常数，且是函数的一个极值点.（Ⅰ）若时，，求实数的取值范围；（Ⅱ）求证：.参考答案：解：（Ⅰ）由题意对定义域内的任意，，为奇函数，当时，，则当时，，由解得，经验证，满足题意；

时，

当时，令，则当时，恒成立，转化为在上恒成立，，令，，在上单调递增，，，在上单调递增，，

即实数的取值范围为.（Ⅱ）由（Ⅰ）可知，当时，，即则令，则，即当时，可得

略22.（12分）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，PA=AB=AD=2，四边形ABCD满足AB⊥AD，BC∥AD且BC=4，点M为PC中点．（1）求证：平面ADM⊥平面PBC；（2）求点P到平面ADM的距离．参考答案：【考点】点、线、面间的距离计算；平面与平面垂直的判定．【分析】（1）取PB中点N，连结MN、AN，证明四边形ADMN为平行四边形，AN⊥平面PBC，可得平面ADM⊥平面PBC；（2）PN⊥平面ADM，即点P到平面ADM的距离为PN，即可求点P到平面ADM的距离．【解答】解：（1）取PB中点N，连结MN、AN，则∵M是PC中点，∴，又∵BC∥AD，∴MN∥A