《9.5 柱、锥、球及其简单组合体(1)》教案(职校)

1、第9第9章立体几何（教案）第9第9章立体几何（教案）课题】9.5柱、锥、球及其简单组合体（一）【教学目标】知识目标：（1）了解棱柱、棱锥的结构特征；（2）掌握棱柱、棱锥面积和体积计算.能力目标：培养学生的观察能力，数值计算能力及计算工具使用技能.【教学重点】正棱柱、正棱锥的结构特征及相关的计算【教学难点】正棱柱、正棱锥的相关计算【教学设计】教材首先介绍了多面体、旋转体的概念然后通过观察模型，说明棱柱、棱锥、圆柱圆锥、球的结构特征及其面积、体积的计算公式正棱柱的侧面积、全面积、体积的计算公式经常使用，不要把侧面积、全面积计算公式记混了侧面都是全等的矩形的直四棱柱不一定是正四棱柱底面是正方形的四棱

2、柱不一定是正四棱柱四棱锥P-ABCD中，如果棱锥的侧棱长相等，那么它一定是正四棱锥如果棱锥的底面是正方形，那么它不一定是正四棱锥例1是求正三棱柱的侧面积和体积的题目，例2是求正三棱锥的侧面积和体积的题目，要记住边长为a的正三角形的面积为Sa2.4【教学备品】教学课件【课时安排】2课时（90分钟）【教学过程】教学过程教师行为学生行为教学意图时间*揭示课题9.5柱、锥、球及其简单组合体【知识回顾】在九年制义务教育阶段，我们学习过直棱柱、圆柱、圆锥、介绍了解0教师行为学生行为教学教师行为学生行为教学意图时间教师行为学生行为教学教师行为学生行为教学意图时间第9第9章立体几何(教案)第9第9章立体几何(

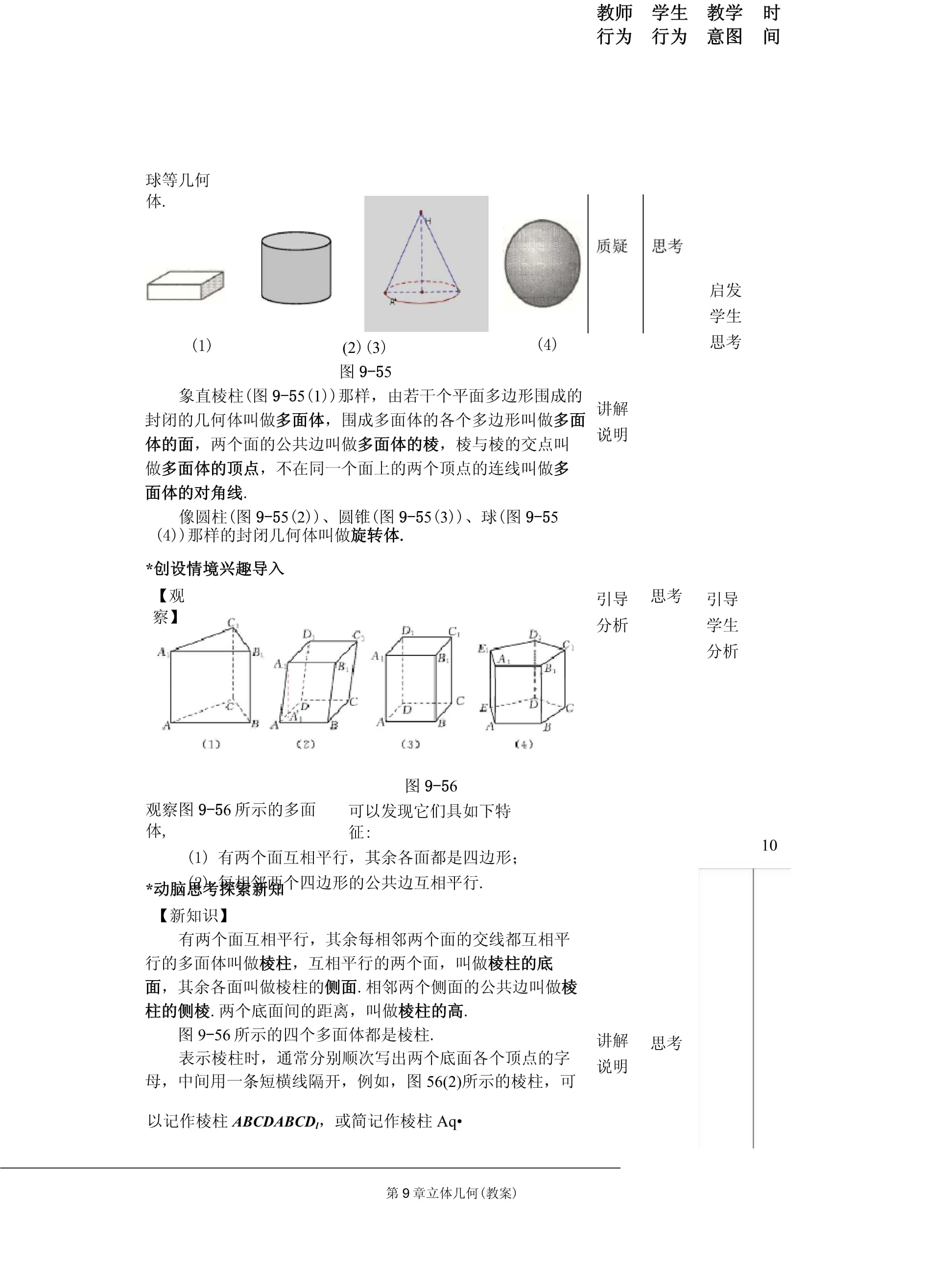
3、教案)球等几何体.(1)(4)(2)(3)图9-55象直棱柱(图9-55(1)那样，由若干个平面多边形围成的封闭的几何体叫做多面体，围成多面体的各个多边形叫做多面体的面，两个面的公共边叫做多面体的棱，棱与棱的交点叫做多面体的顶点，不在同一个面上的两个顶点的连线叫做多面体的对角线.像圆柱(图9-55(2)、圆锥(图9-55(3)、球(图9-55(4)那样的封闭几何体叫做旋转体.*创设情境兴趣导入【观察】图9-56可以发现它们具如下特征:有两个面互相平行，其余各面都是四边形；每相邻两个四边形的公共边互相平行.观察图9-56所示的多面体,*动脑思考探索新知【新知识】有两个面互相平行，其余每相邻两个面

4、的交线都互相平行的多面体叫做棱柱，互相平行的两个面，叫做棱柱的底面，其余各面叫做棱柱的侧面.相邻两个侧面的公共边叫做棱柱的侧棱.两个底面间的距离，叫做棱柱的高.图9-56所示的四个多面体都是棱柱.表示棱柱时，通常分别顺次写出两个底面各个顶点的字母，中间用一条短横线隔开，例如，图56(2)所示的棱柱，可以记作棱柱ABCDABCDl，或简记作棱柱Aq讲解说明引导分析讲解说明思考思考启发学生思考引导学生分析10第9第9章立体几何(教案)第9第9章立体几何(教案)教学过程教师行为学生行为教学意图时间经常以棱柱底面多边形的边数来命名棱柱，如图9-56所示的棱柱依次为三棱柱、四棱柱、五棱柱.侧棱与底面斜父

5、的棱柱叫做斜棱柱，如图9-56(2)；侧棱与底面垂直的棱柱叫做直棱柱，如图9-56(1)；底面是正多边形的直棱柱叫做正棱柱，如图9-56(3)和(4)，分别为正四棱柱和正五棱柱.正棱柱有下列性质：引领理解(1)侧棱垂直于底面，各侧棱长都相等，并且等于正棱分析柱的咼；(2)两个底面中心的连线是正棱柱的咼.想一想如果直四棱柱的侧面都是全等的矩形，它是不是正四棱柱？如果四棱柱的底面是正方形，它是不是正四棱柱？带领【新知识】学生正棱柱所有侧面的面积之和，叫做正棱柱的侧面积.正棱分析柱的侧面积与两个底面面积之和，叫做正棱柱的全面积.仔细!r分析记忆关键语句图9-57观察正棱柱的表面展开图(图9-57)，

6、可以得到正棱柱的侧面积、全面积计算公式分别为S=ch(9.1)正棱柱侧S=ch+2S(9.2)正棱柱全底其中，表示正棱柱底面的周长，h表示正棱柱的咼，冷表示正棱柱底面的面积.可以得到正棱柱的体积计算公式为(公式推导略)V=Sh(9.3)正棱柱底其中，S底表示正棱锥的底面的面积，h是正棱锥的高.25*巩固知识典型例题教师行为学生行为教学教师行为学生行为教学意图时间教师行为学生行为教学教师行为学生行为教学意图时间第9第9章立体几何（教案）第9第9章立体几何（教案）【知识巩固】例1已知一个正三棱柱的底面边长为4cm,高为5cm,求这个正三棱柱的侧面积和体积.解正三棱锥的侧面积为S狈ch=3X4X5=

7、60（cm2）.由于边长为4cm的正三角形面积为x42=43（cm2）,4所以正三棱柱的体积为V=S底h=43x5=203(cm3).说明强调引领观察思考通过例题进一步领会讲解说明主动求解g|丈：，心*：-；讲解说明主动求解g|丈：，心*：-；r-M，-2/_*=忙”-A崎-TBirM*：-三坤并工具九两昭记工|!qlEJJl*naffl*BTA*正書卯工|!卜亶tEH田畑庄直$立工Bf讲解说明思考理解带领学生思考【小提示】边长为a的正三角形的面积为S=a24【软件连接】利用几何画板可以方便地作出棱柱的直观图形.方法是：首先选中所以绘制棱柱的名称（图9-58），然后选择合适的位置，点击并拖动，

8、即可得到棱柱的直观图形（图9-59）,最后再标注字母.图958圈箱疏_三亍二fLTl：_Tliv目耳辿习存:妄口:丄千門上35质疑引导分析思考圈箱疏_三亍二fLTl：_Tliv目耳辿习存:妄口:丄千門上35质疑引导分析思考启发学生思考图9-59*创设情境兴趣导入观察图9-60所示的多面体，可以发现它们具如下特征：有一个面是多边形，其余各面都是三角形，并且这些三角形有一个公共顶点.40图9-6040*动脑思考探索新知【新知识】具备上述特征的多面体叫做棱锥.多边形叫做棱锥的底面（简称底），有公共顶点的三角形面叫做棱锥的侧面，各侧面的公共顶点叫做棱锥的顶点，顶点到底面的距离叫做棱锥的高.底面是三角形

9、、四边形、的棱锥分别叫做三棱锥、四棱锥、通常用表示底面各顶点的字母来表示棱锥.例如，图9-60（2）中的棱锥记作：棱锥SABCD.思考带领学生分析底面是正多边形，其余各面是全等的等腰三角形矩形的棱讲解锥叫做正棱锥.图9-60中（1）、（2）分别表示正三棱锥、正说明四棱锥.思考带领学生分析正棱锥有下列性质：（1）各侧棱的长相等；（2）各侧面都是全等的等腰三角形.各等腰三角形底边教师行为学生行为教学教师行为学生行为教学意图时间第9第9章立体几何(教案)80第80第9章立体几何（教案）教学过程教师行为学生行为教学意图时间上的高都叫做正棱锥的斜高；顶点到底面中心的连线垂直与底面，是正棱锥的咼；正棱锥的

10、咼、斜咼与斜咼在底面的射影组成一个直引领角三角形；分析理解(5)正棱锥的咼、侧棱与侧棱在底面的射影也组成一个直角三角形.【想一想】四棱锥P-ABCD中，如果棱锥的侧棱长相等，那么它是不是正四棱锥？如果棱锥的底面是正方形，那么它是不是正四棱锥？【新知识】讲解思考#V/!/说明带领学生(s分析/图9-61观察正棱锥的表面展开图(图9-61)，可以得到正棱锥的引领记忆侧面积、全面积(表面积)计算公式分别为1分析S=二chh(9.4)正棱锥侧2S=-chh+S.(9.5)正棱锥全2底其中，c表示正棱锥底面的周长，h是正棱锥的斜高，S底表示正棱锥的底面的面积，h是正棱锥的咼.52*创设情境兴趣导入带领【

11、实验】质疑思考学生八厂准备好同底等高的正三棱锥与正三棱柱形容器，将正三棱锥容器中装满沙子，然后倒入正三棱柱形状的容器中，发现：连续倒三次正好将正三棱柱容器装满.分析57*动脑思考探索新知【新知识】实验表明，对于同底等高的棱锥与棱柱，棱锥的体积是棱柱体讲解理解带领积的三分之一.即说明学生分析V=-Sh.正棱锥3底(9.6)其中，S底表示正棱锥的底面的面积，h是正棱锥的高.记忆62*巩固知识典型例题【知识巩固】例2如图9-62，正三棱锥P-ABC中，点0是底面中心，斜高PD=13cm.求它的侧面积、体积（面积精P0=12cm,cm.确至到0.1cm2，体积精确到1cm3）.图9-62解在正三棱P-

12、ABC（图9-62）中，高P0=12cm,斜高PD=13在直角三角形POD中，cm.0D=；PD2PO2=132122=5(cm).在底面正三角形ABC中，CD=3OD=15（cm）.所以底面边长为AC=10、3cm.所以侧面积与体积分别约为S=1ch二-x3x107亍x13心337.7(cm2).侧22V=-Sh=-xx(10：3)2xsin60 x12520(cm3).正棱锥3底32*运用知识强化练习设正三棱柱的高为6,底面边长为4,求它的侧面积、全面积及体积.正四棱锥的高是a,底面的边长是2a,求它的全面积与体积.*理论升华整体建构说明强调引领讲解说明提问巡视指导观察思考主动求解思考解答

13、通过例题进一步领会及时了解学生知识掌握情况72教学教师学生教学时过程行为行为意图间思考并回答下面的问题：正棱柱的侧面积、全面积、体积公式，正棱锥的侧面积、质疑全面积、体积公式？及时结论：回答了解学生S=ch；S=ch+2S；正棱柱侧正棱柱全底归纳知识V=Sh；正棱柱底强调掌握情况s=-ch；s=1ch+s；正棱锥侧2正棱锥全2底V=1Sh.正棱锥3底83*归纳小结强化思想本次课学了哪些内容？重点和难点各是什么？引导回忆*自我反思目标检测本次课采用了怎样的学习方法？你是如何进行学习的？你的学习效果如何？提问反思检验学生设正二棱柱的咼为6,底面边长为4,求它的侧面积、全巡视动手学习面积及体积.指导求解效果89*继续探索活动探究(1)读书部分：教材说明记录分层、/47FFT(2)书面作业：教材习题9.5A组(必做)；9.5B组(选次要求做)(3)实践调查：用发现的眼睛寻找生活中的正棱柱实例90项目反思点学生知识、技能的掌握情况学生是否真正理解有关知识；是否能利用知识、技能解决问题；在知识、技能的掌握上存在哪些问题；学生的情感态度学生是否参与有关活动；教师教学后记】第9第9章立体