



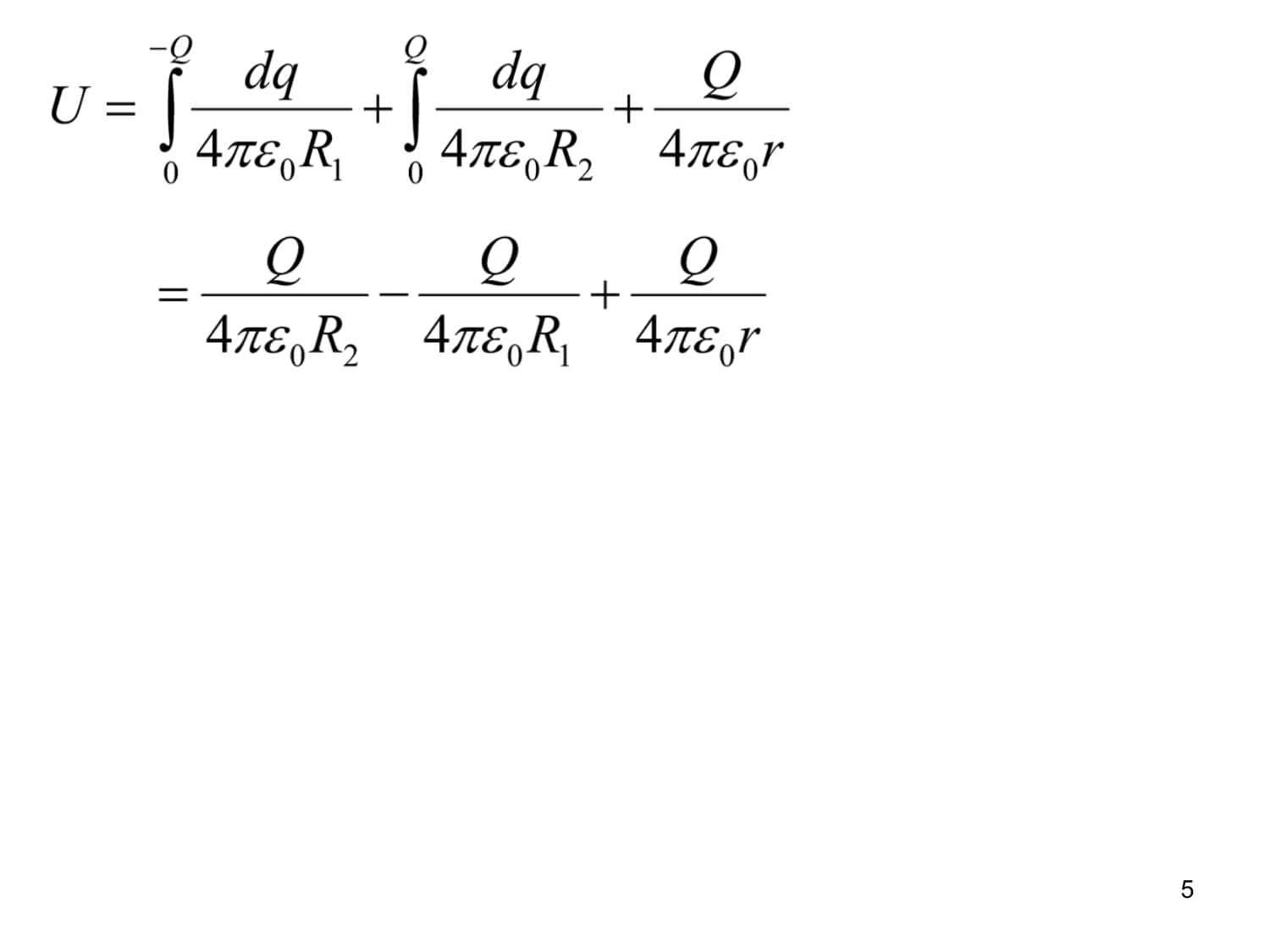
版权说明:本文档由用户提供并上传,收益归属内容提供方,若内容存在侵权,请进行举报或认领
文档简介
1(1)如图所示,一沿x轴放置的“无限长”分段均匀带电直线,电荷线密度分别为+λ(x<0)和-λ(x>0),则oxy坐标平面上点(0,a)的场强=
。解:根据对称性可知:电荷元dq在(0,a)点产生的电场强度的大小为:一、填空题1(1)如图所示,一沿x轴放置的“无限长”分段均匀带电直线,223(2)两无限大平板A、B。A带电荷面密度为,B带电荷面密度-2,则A外侧场强大小为
、B外测场强大小为
、AB之间场强大小为
。解:A板左侧B板右侧两极板间3(2)两无限大平板A、B。A带电荷面密度为,B带电荷面43、导体球壳的内外半径分别为R1和R2,若在距球心O为r的P点放置一点电荷Q,如图所示,则导体球壳的电势
;中心O点的电势
。解:静电平衡时球壳的外表面带电量与p点的电量相同,且由于球壳的外表面曲率半径相同,电荷密度也相同,即电荷是均匀分布在球面上的。电势为中心O点的电势是p点的电荷、内表面R1和外表面R2的电荷共同贡献的由电势的叠加原理:43、导体球壳的内外半径分别为R1和R2,若在距球心O为r556解用补偿法:设想圆柱原来没有窄缝,用宽度为l,面电荷密度为-σ的带电窄条补在窄缝处,由于圆柱面对场强的贡献为0,p点的场强由该窄条产生,该窄条的电荷线密度为0点的场强为6解用补偿法:设想圆柱原来没有窄缝,用宽度为l,面电荷密度为7取0点的电势为0,p点的场强由电势7取0点的电势为0,p点的场强由电势8电源接通情况下电容器两端电压不变:分析:电源断开情况下电容器极板上带电量不变:(3)一空气平行板电容器,接上电源后,两极板上的电荷面密度分别为
。在保持电源接通情况下,将相对介电常数为εr的各向同性均匀电介质充满其中,忽略边缘效应,介质中的场强大小应为
。而断开电源再充满该种介质,则介质中的场强大小又为
。8电源接通情况下电容器两端电压不变:分析:电源断开情况下电容9计算题1、一细玻璃棒弯成半径为R的半圆形,沿上半部均匀分布有电荷+q,沿下半部均匀分布有电荷-q,求半圆中心0处的电场强度E。解1:由对称性,带电荷为+q的1/4圆弧产生的电场在第四象限。带电荷为-q的1/4圆弧产生的电场方向在第三象限。它们的合场强沿-y取电荷元如图则对上式积分且考虑到两个1/4圆弧产生的场强y分量大小相同:9计算题1、一细玻璃棒弯成半径为R的半圆形,沿上半部均匀分布10把λ=q/(πR/2)代入上式得解2:先计算1/4圆弧的场强,由对称性可知场强的方向在从圆心到圆弧中点连线上,电荷线密度λ同上。取如图所示的电荷元,产生的电场分量积分得10把λ=q/(πR/2)代入上式得解2:先计算1/4圆弧11结果如图。电场强度沿–y方向同样可以得到-q的场强,则合场强为:11结果如图。电场强度沿–y方向同样可以得到-q的场强,122、地球表面上方电场方向向下,大小可能随高度改变,如图所示。设在地面上方100m高处场强为150N/C,300m高处场强为100N/C。试由高斯定律求在这两个高度之间的平均体电荷密度,以多余的或缺少的电子数密度表示。
解:在空气中取一柱形高斯面,上表面在300m处,场强为E1,下表面在100m处,场强为E2,截面积为s。由高斯定理得到电荷密度122、地球表面上方电场方向向下,大小可能随高度改变,如图所13单位体积内的电子数为由于所带的是正点荷,空气中缺少电子。13单位体积内的电子数为由于所带的是正点荷,空气中缺少电子。143、如图所示,三块互相平行的均匀带电大平面,面电荷密度为σ1=1.2×10-4C/m2,σ2=2×10-5C/m2,σ3=1.1×10-4C/m2。A点与平面Ⅱ相距为5.0cm,B点与平面Ⅱ相距7.0cm。(1)计算A、B两点的电势差;(2)设把电量qo=-1.0×10-8C的点电荷从A点移到B点,外力克服电场力做多少功?
解:取x轴如图。设平面ⅠⅡ间的场强EA,平面ⅡⅢ的场强EB。由叠加原理取平面Ⅱ为电势0点,AⅡ距离为d1,BⅡ距离为d2.143、如图所示,三块互相平行的均匀带电大平面,面电荷密度为15电场力做功15电场力做功164、一导体球半径为R1,其外同心地罩以内、外半径分别为R2和R3的厚导体球壳,此系统带电后内球电势为U1,外球所带总电量为Q。求此系统各处的电势和电场分布。
解:设导体球带电量为q,则由电势的叠加原理,导体球的电势是球壳的电势与内球与外球间的电势差之和为内球带电量为164、一导体球半径为R1,其外同心地罩以内、外半径分别为17利用上式可以求出场强、电势17利用上式可以求出场强、电势1818195、一个接地的导体球,半径为R,原来不带电。今将一点电荷q放在球外距球心的距离为r的地方,求球上的感生电荷总量。解:设q放入后在导体球上感生的电荷总量为Q,则由电势的叠加原理,导体球球心的电势为由于导体球接地电势等0,得到感生电荷总量195、一个接地的导体球,半径为R,原来不带电。今将一点电荷206、为了测量电介质材料的相对介电常量,将一块厚为1.5cm的平板材料慢慢地插进一电容器的距离为2.0cm的两平行板之间。在插入过程中,电容器的电荷保持不变。插入之后,两板间的电势差减少为原来的60%,求电介质的相对介电常量多大?解:设电容器极板间距为d,电荷密度为σ,电介质未插入时,极板间的场强、电势为:若介质的厚度为T,插入介质后介质中的场强这时两板间的电势差206、为了测量电介质材料的相对介电常量,将一块厚为1.5c21(1)如图所示,一沿x轴放置的“无限长”分段均匀带电直线,电荷线密度分别为+λ(x<0)和-λ(x>0),则oxy坐标平面上点(0,a)的场强=
。解:根据对称性可知:电荷元dq在(0,a)点产生的电场强度的大小为:一、填空题1(1)如图所示,一沿x轴放置的“无限长”分段均匀带电直线,22223(2)两无限大平板A、B。A带电荷面密度为,B带电荷面密度-2,则A外侧场强大小为
、B外测场强大小为
、AB之间场强大小为
。解:A板左侧B板右侧两极板间3(2)两无限大平板A、B。A带电荷面密度为,B带电荷面243、导体球壳的内外半径分别为R1和R2,若在距球心O为r的P点放置一点电荷Q,如图所示,则导体球壳的电势
;中心O点的电势
。解:静电平衡时球壳的外表面带电量与p点的电量相同,且由于球壳的外表面曲率半径相同,电荷密度也相同,即电荷是均匀分布在球面上的。电势为中心O点的电势是p点的电荷、内表面R1和外表面R2的电荷共同贡献的由电势的叠加原理:43、导体球壳的内外半径分别为R1和R2,若在距球心O为r25526解用补偿法:设想圆柱原来没有窄缝,用宽度为l,面电荷密度为-σ的带电窄条补在窄缝处,由于圆柱面对场强的贡献为0,p点的场强由该窄条产生,该窄条的电荷线密度为0点的场强为6解用补偿法:设想圆柱原来没有窄缝,用宽度为l,面电荷密度为27取0点的电势为0,p点的场强由电势7取0点的电势为0,p点的场强由电势28电源接通情况下电容器两端电压不变:分析:电源断开情况下电容器极板上带电量不变:(3)一空气平行板电容器,接上电源后,两极板上的电荷面密度分别为
。在保持电源接通情况下,将相对介电常数为εr的各向同性均匀电介质充满其中,忽略边缘效应,介质中的场强大小应为
。而断开电源再充满该种介质,则介质中的场强大小又为
。8电源接通情况下电容器两端电压不变:分析:电源断开情况下电容29计算题1、一细玻璃棒弯成半径为R的半圆形,沿上半部均匀分布有电荷+q,沿下半部均匀分布有电荷-q,求半圆中心0处的电场强度E。解1:由对称性,带电荷为+q的1/4圆弧产生的电场在第四象限。带电荷为-q的1/4圆弧产生的电场方向在第三象限。它们的合场强沿-y取电荷元如图则对上式积分且考虑到两个1/4圆弧产生的场强y分量大小相同:9计算题1、一细玻璃棒弯成半径为R的半圆形,沿上半部均匀分布30把λ=q/(πR/2)代入上式得解2:先计算1/4圆弧的场强,由对称性可知场强的方向在从圆心到圆弧中点连线上,电荷线密度λ同上。取如图所示的电荷元,产生的电场分量积分得10把λ=q/(πR/2)代入上式得解2:先计算1/4圆弧31结果如图。电场强度沿–y方向同样可以得到-q的场强,则合场强为:11结果如图。电场强度沿–y方向同样可以得到-q的场强,322、地球表面上方电场方向向下,大小可能随高度改变,如图所示。设在地面上方100m高处场强为150N/C,300m高处场强为100N/C。试由高斯定律求在这两个高度之间的平均体电荷密度,以多余的或缺少的电子数密度表示。
解:在空气中取一柱形高斯面,上表面在300m处,场强为E1,下表面在100m处,场强为E2,截面积为s。由高斯定理得到电荷密度122、地球表面上方电场方向向下,大小可能随高度改变,如图所33单位体积内的电子数为由于所带的是正点荷,空气中缺少电子。13单位体积内的电子数为由于所带的是正点荷,空气中缺少电子。343、如图所示,三块互相平行的均匀带电大平面,面电荷密度为σ1=1.2×10-4C/m2,σ2=2×10-5C/m2,σ3=1.1×10-4C/m2。A点与平面Ⅱ相距为5.0cm,B点与平面Ⅱ相距7.0cm。(1)计算A、B两点的电势差;(2)设把电量qo=-1.0×10-8C的点电荷从A点移到B点,外力克服电场力做多少功?
解:取x轴如图。设平面ⅠⅡ间的场强EA,平面ⅡⅢ的场强EB。由叠加原理取平面Ⅱ为电势0点,AⅡ距离为d1,BⅡ距离为d2.143、如图所示,三块互相平行的均匀带电大平面,面电荷密度为35电场力做功15电场力做功364、一导体球半径为R1,其外同心地罩以内、外半径分别为R2和R3的厚导体球壳,此系统带电后内球电势为U1,外球所带总电量为Q。求此系统各处的电势和电场分布。
解:设导体球带电量为q,则由电势的叠加原理,导体球的电势是球壳的电势与内球与外球间的电势差之和为内球带电量为164、一导体球半径为R1,其外同心地罩以内、外半径分别为37利用上式可以求出场强、电势17利用上式可以求出场强、电势3818395、一个接地的导体球,半径为R,原来不带电。今将一点电荷q放在球外距球心的距离为r的地方,求球上的感生电荷总量。解:设q放入后在导体球上感生的电荷总量为Q,则由电势的叠加原理,导体球球心的电势为由于导体球接地电势等0,得到
温馨提示
- 1. 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
- 2. 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
- 3. 本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
- 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
- 5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
- 6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
- 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
最新文档
- 2025年中国配套设备行业发展前景预测及投资战略研究报告
- 2025年中国耐振压力表行业市场深度研究及投资规划建议报告
- 中国化探仪器行业市场调研分析及投资前景预测报告
- 2025年中国中低端白酒行业市场深度分析及投资战略规划报告
- 2025年中国猪午餐肉行业市场前景预测及投资战略研究报告
- 2021-2026年中国纸管机市场运营态势及发展前景预测报告
- 2025年中国木纹办公家具行业市场调查研究及发展战略规划报告
- 2025年中国味精行业竞争格局分析及投资规划研究报告
- 中国常压储罐行业发展监测及发展趋势预测报告
- 呜呜奶奶我想你了600字(15篇)
- DB4201∕T 645-2021 房地产经纪服务规范
- 拨叉综合课程设计
- 压铸件QC工程图
- pH 值对柠檬酸缓凝效果影响的研究
- 学校物业服务监督及处罚办法
- 1104基础报表填报说明(最新)
- 老旧小区改造技术标-
- 705型试验台技术条件及说明书
- 天麻、猪苓种植技术教学大纲
- 汉字的起源与演变过程.ppt
- 2011年吉林省初中生物会考试题

评论
0/150
提交评论