自动控制技术第4章控制系统频域分析

1、 第四章第四章 频率特性分析频率特性分析Frequency Characteristic Analysis u时域法时域法: 是研究当给定输入信号后，其输出随时间变是研究当给定输入信号后，其输出随时间变 化的化的情况，所用的方法是通过拉氏变换求解情况，所用的方法是通过拉氏变换求解 微分方程式。通微分方程式。通过分析线性系统的过度过程，获得系统的动态特性。过分析线性系统的过度过程，获得系统的动态特性。u频域法频域法: 是利用系统对不同频率正弦信号的响应，来是利用系统对不同频率正弦信号的响应，来 研究研究系统的动态和静态性能。系统的动态和静态性能。u频率特性法是分析线性系统的工程实用方法。频率特性

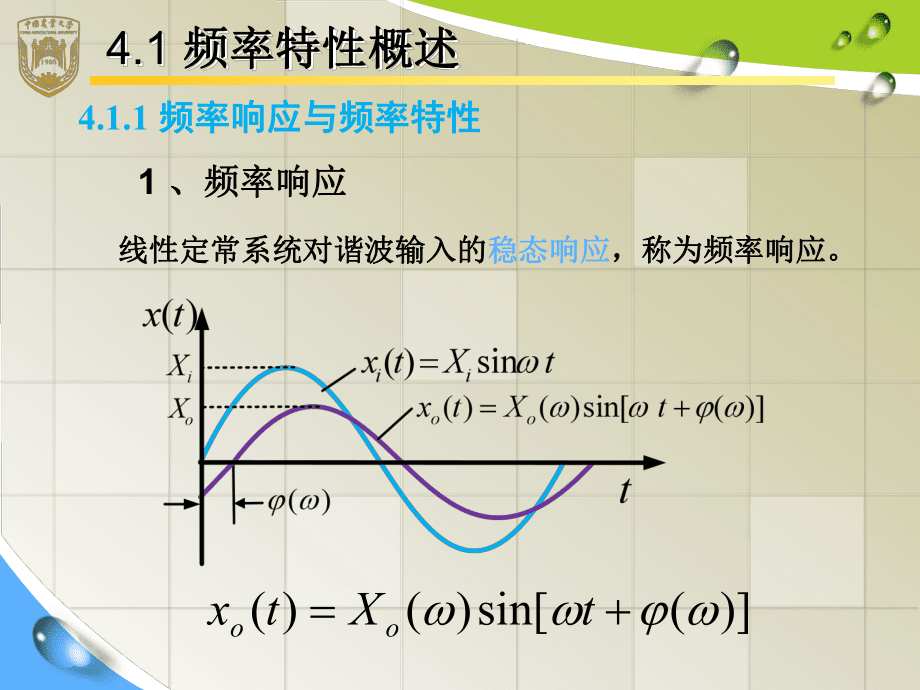
2、法是分析线性系统的工程实用方法。u频率特性反映系统的稳态性能、稳定性、暂态性能。频率特性反映系统的稳态性能、稳定性、暂态性能。 4.1 频率特性概述频率特性概述4.1.1 频率响应与频率特性频率响应与频率特性 1 、频率响应、频率响应 线性定常系统对谐波输入的线性定常系统对谐波输入的稳态响应稳态响应，称为频率响应。，称为频率响应。)(sin)()(tXtxoo例例1 设传递函数为设传递函数为 1)(TsKsG解：设输入信号为解：设输入信号为 22)(sin)(sXsXtXtxiiii则输出为则输出为 221)()()(sXTsKsXsGsXiio)arctansin(11)(22/22TtTK

3、XeTKTXtxiTtio系统的稳态响应系统的稳态响应)arctansin(1)(22TtTKXtxio时间响应为时间响应为 系统输出的幅值系统输出的幅值 221)(TKXXio 系统输出的相位系统输出的相位 Tarctan)(u频率响应频率响应只是时间响应的一个只是时间响应的一个特例特例。u当当谐波频率不同时，其输出的幅值与相位也不同。谐波频率不同时，其输出的幅值与相位也不同。幅频特性：幅频特性：线性系统在谐波输入作用下，其稳定输出与输入线性系统在谐波输入作用下，其稳定输出与输入的幅值比，即的幅值比，即 反映系统对不同频率正弦信号的稳态衰减（或放大）特性。反映系统对不同频率正弦信号的稳态衰减

4、（或放大）特性。相频特性：相频特性：稳态输出信号与输入信号的相位差，即稳态输出信号与输入信号的相位差，即 。表示系统在不同频率正弦信号下输出的相位移。表示系统在不同频率正弦信号下输出的相位移。幅频特性和相频特性总称为频率特性。幅频特性和相频特性总称为频率特性。相位相位逆时针逆时针为正为正 ，顺时针顺时针为负为负 。相位相位超前超前为为正正 ，相位滞后相位滞后为为负负 。对物理系统相位一般都是滞后的对物理系统相位一般都是滞后的。ioXXA)()(记作记作)()(A或或)()(jeA2、频率特性、频率特性)(0)(0)(0)(0)(4.1.2 频率特性与传递函数的关系频率特性与传递函数的关系设系统

5、的微分方程为设系统的微分方程为)()()()()()()()(01)1(1)(01)1(1)(txbtxbtxbtxbtxatxatxatxaiimimmimoononnon系统传递函数为系统传递函数为onnnnommmmioasasasabsbsbsbsXsXsG111111)()()(当输入信号为当输入信号为tXtxiisin)(22)(sXsXii即即系统的输出系统的输出 22111111)()()(sXasasasabsbsbsbsXsGsXionnnnommmmio若系统无重极点若系统无重极点)()(*1jsBjsBssAsXniiio)*()(1tjtjnitsioeBBeeAtx

6、i稳态响应为稳态响应为 tjtjoeBBetx*)(若若系统含有系统含有 重极点重极点 ，则输出，则输出 将含有将含有 。对。对于稳定系统，由于于稳定系统，由于 的实部为负，的实部为负， 的增长没有的增长没有 的衰减快。的衰减快。所以所以 的各项随着的各项随着 也趋于零。因此稳态响应不管也趋于零。因此稳态响应不管是否有重极点，其稳态响应不变。是否有重极点，其稳态响应不变。 ) 1, 2 , 1(kjettskjkttsjetskjettjXejGjXjGjsXsGjsjsjsXsGBijGjijsijsi2)(2)()()()()()()( jXejGjXjGBijGji2)(2)(*)(则稳

7、态响应为则稳态响应为 )(sin)(2)()()()(jGtXjGjeeXjGtxijGtjjGtjiokjsjstskjet根据频率特性定义，系统根据频率特性定义，系统的幅频和相频特性分别为的幅频和相频特性分别为 )()(| )(|)()(jGjGXiXoA故故)(| )(|)(jGjejGjG就是系统的频率特性。量纲同传递函数。就是系统的频率特性。量纲同传递函数。由于由于 是是一个复变函数，可以写成实部和虚部之和，一个复变函数，可以写成实部和虚部之和，即即)v()u()ImG(j)ReG(j)G(jj实频特性实频特性 虚频特性虚频特性)u()v()G(j4.1.3 频率特性频率特性的求法的

8、求法 1、根据系统的频率响应来求取、根据系统的频率响应来求取22)(sXsXii)()(221sXsGLtxio从稳态响应中可得到频率响应的幅值和相位。从稳态响应中可得到频率响应的幅值和相位。 )arctansin(1)(22TtTKXtxio例例1时间响应为时间响应为 221)()(TKXXAioTarctan)(例例1的稳态响应为的稳态响应为 2、 将传递函数中的将传递函数中的s 换为换为j（s=j）来求取）来求取将将系统的传递函数系统的传递函数G(s)中的中的s换为换为j，即为系统的频率特性。，即为系统的频率特性。)()(arctan)()()()()(sin)()()(cos)()()

9、()()(sin)()(cos)()()()()(22)(uvvuAAvAueAjGjAAjGjvujGj相频特性：幅频特性：虚频特性：实频特性：指数式：三角式：代数式：频率特性三种表达方式例例 系统系统的的传递函数为传递函数为TjjseTKjTKsGjGarctan2211)()(221)()(TKXXAioTarctan)()arctansin(1)(sin)()(22TtTKXsGtsGXtxiio幅频特性为幅频特性为 频率响应为频率响应为 解：频率特性为解：频率特性为 相频特性为相频特性为 1)(TsKsG3 、用试验方法求取、用试验方法求取 首先，改变输入谐波首先，改变输入谐波信号信

10、号 的频率的频率 ，并测出与相应并测出与相应的输出幅的输出幅值值 与相位与相位 。 然后，作出然后，作出幅值幅值比比 对频率对频率 的的函数曲线，即幅函数曲线，即幅频特性曲线频特性曲线； 作出相位作出相位 对频率对频率 的的函数曲线，即相频特性曲线。函数曲线，即相频特性曲线。tjieX)(oX)(ioXX/ )()(4.1.4 频率特性频率特性的特点和作用的特点和作用 (1) 有有 而而当当 时，时， ， 且且 故故 这表明系统的频率特性就是这表明系统的频率特性就是单位脉冲响应函数单位脉冲响应函数 的的Fourier变换，变换，即即 的的频谱频谱。)()()(sXsGsXio)()()(jXj

11、GjXio)()(tsxi)()(twtxo1)()(tFjXi)()(jGjXo)()(jGtwF)(tw)(tw（2） 时间响应分析主要分析线性系统时间响应分析主要分析线性系统过渡过程过渡过程，获取系统，获取系统的动态特性；而频率特性分析不同的谐波输入时系统的的动态特性；而频率特性分析不同的谐波输入时系统的稳稳态响应态响应，获取系统的动态特性。，获取系统的动态特性。（3） 在研究系统的结构及参数的变化对系统性能的影响时在研究系统的结构及参数的变化对系统性能的影响时，许多情况，在，许多情况，在频域中分析要容易频域中分析要容易得多。特别是频率特性得多。特别是频率特性可方便地判别系统的可方便地判

12、别系统的稳定性和稳定储备量稳定性和稳定储备量，参数选择参数选择或或系系统校正统校正，使系统尽可能达到预期的性能指标。根据频率特，使系统尽可能达到预期的性能指标。根据频率特性，易于确定系统性，易于确定系统频率范围频率范围。（4）若线性系统的）若线性系统的阶次较高阶次较高，特别是对于不能用分析法得出，特别是对于不能用分析法得出微分方程的系统，在时域中分析系统的性能很困难，采用微分方程的系统，在时域中分析系统的性能很困难，采用频频率特性分析率特性分析就很容易。就很容易。（5）系统在输入信号的同时，在某些频带中有着严重的噪声系统在输入信号的同时，在某些频带中有着严重的噪声干扰，则对系统采用频率特性分析

13、法可设计出合适的干扰，则对系统采用频率特性分析法可设计出合适的通频带通频带，以抑制噪声的影响以抑制噪声的影响 。 4.2 频率特性的图示方法频率特性的图示方法4.2.1频率特性的极坐标图频率特性的极坐标图频率特性的极坐标图是把频率特性的极坐标图是把看成一个参变量，将频率特性的看成一个参变量，将频率特性的幅频特性和相频特性同时画在复平面上。幅频特性和相频特性同时画在复平面上。当输入信号的频率当输入信号的频率由由0变化时变化时,矢量矢量G(j)的端点在复平的端点在复平面上移动的轨迹叫极坐标图或称为乃氏（面上移动的轨迹叫极坐标图或称为乃氏（Nyquist）图。）图。 )()(arctan)()()(

14、)()()()()(22)(uvvuAeAjvujGj1 典型环节的典型环节的Nyquist图图（1）比例环节）比例环节0)()()(jGKjGKjG其极坐标图是其极坐标图是实轴上实轴上K这一点这一点。（2 2）积分环节）积分环节90)(, 0)(,90)(,)(, 090)(1)(1)(jGjGjGjGjGjGjjG其极坐标图是其极坐标图是虚轴的下半轴，由无穷远点指向原点虚轴的下半轴，由无穷远点指向原点。（3 3） 微分环节微分环节90)(,)(,90)(, 0)(, 090)()()(jGjGjGjGjGjGjjG其极坐标图是其极坐标图是虚轴的上半轴，由原点指向无穷远点虚轴的上半轴，由原点

15、指向无穷远点。（4 4） 惯性环节惯性环节90)(, 0)(,45)(,2/)(,/10)(,)(, 0arctan)(1)(1)(22jGjGjGKjGTjGKjGTjGTKjGjTKjG90)(, 0)(,45)(,2/)(,/10)(,)(, 0arctan)(1)(1)(22jGjGjGKjGTjGKjGTjGTKjGjTKjG其极坐标图为其极坐标图为一下半圆一下半圆 222211()111TG jjjTTT222222222)21()21(0)()(11)() 1 ()2()2()()() 1 (11)(vuuvuuvuTuvTu代把证明过程证明过程习题习题ssG01. 011)()

16、 1 (ssG01. 011)()2(101. 01)() 3(ssG1(4) ( )0.011G ss（5 5）一阶微分环节（导前环节）一阶微分环节（导前环节）90)(,)(,45)(,2)(,/10)(, 0)(, 0arctan)(1)(1)(22jGjGjGjGTjGjGTjGTjGjTjG22() 1()1()arctan0,()1,()01/ ,()2,()45,(),()90G jjTG jTG jTG jG jT G jG jG jG j （6 6）振荡环节）振荡环节222222222222( )2()2/1()(1)2()(1)42()arctan10,0,()1,()01,

17、()1/ 2 ,()90,()0,()180nnnnnnnnG sssG jjG jjKG jG jG jG jG jG jG jG j 180)(, 0)(,90)(,2/1)(, 10)(, 1)(, 0, 012arctan)(4)1 ()(2)1 (1)(/2)(2)(222222222222jGjGjGjGjGjGjGKjGjjGjjGsssGnnnnnnnn180)(, 0)(,90)(,2/1)(, 10)(, 1)(, 0, 012arctan)(4)1 (1)(2)1 (1)(/2)(2)(222222222222jGjGjGjGjGjGjGjGjjGjjGsssGnnnnn

18、nnn2212121rnrMu当当 时时，幅频特性，幅频特性在频率在频率为为 (或或频率频率比比 )处出现处出现峰值，此峰值，此峰值为谐峰值为谐振振峰值，峰值， 为为谐振谐振频率。频率。u 时，时， ，谐振峰值为谐振峰值为1，即谐，即谐振峰值不存在，振峰值不存在， 为为最佳阻尼比。最佳阻尼比。707. 0rnrr/r0r707. 0707. 0不同阻尼比振荡环节不同阻尼比振荡环节Nyquist图图（7 7）延时环节）延时环节 )(1)(sincos)()(jGjGjejGesGjs实际实际系统系统理想理想系统系统 2 2 、NyquistNyquist图的一般形式图的一般形式)()(33221

19、1jvujvujvuKsG）（232222221231)(vuvuvuKjG对于多阶系统对于多阶系统幅频特性幅频特性332211arctanarctanarctan)(uvuvuvjG相频特性相频特性) 1()(TssKsG)1 (1)1 (11)1 ()(2222TKjTKTjTjKjTjKjG180)(, 0)(,90)(,)(, 0arctan90)(1)(22jGjGjGjGTjGTKjG例例1) 1-()(TssKsG)1 (1)1- (11)1- ()(2222TKjTKTjTjKjTjKjG180)(, 0)(,90)(,)(, 0arctan90)arctan180(90)(1

20、)(22jGjGjGjGTTjGTKjG例例2) 1)(1()(212sTsTsKsG例例3 3360)(, 0)(,180)(,)(, 0arctanarctan180)(11)()1)(1 ()()(212222212212jGjGjGjGTTjGTTKjGjTjTjKjG360)(, 0)(,180)(,)(, 0arctanarctan180)(11)()1)(1 ()()(212222212212jGjGjGjGTTjGTTKjGjTjTjKjG)() 1() 1()(2121TTsTssTKsG例例4360)(,0)(,180)(,)(,0arctan90arctan)(11)()

21、1 ()1 ()(2122222121jGjGjGjGTTjGTTKjGjTjjTKjG90)(, 0)(,90)(,)(, 0arctan90arctan)(11)()1 ()1 ()(2122222121jGjGjGjGTTjGTTKjGjTjjTKjG)50)(2 . 0(55)(sssssG）（-12-10-8-6-4-20-200-150-100-50050100150200Nyquist DiagramReal AxisImaginary Axis-4-3.5-3-2.5-2-1.5-1-0.50-4-3-2-101234Nyquist DiagramReal AxisImagin

22、ary Axis Bode图表示频率特性的优点图表示频率特性的优点（1）可将串联环节幅值的乘、除，化为幅值的加、）可将串联环节幅值的乘、除，化为幅值的加、减，因而简化了计算与作图过程。减，因而简化了计算与作图过程。（2）可用近似方法作图。）可用近似方法作图。（3）分别作出各个环节的）分别作出各个环节的Bode图，然后用叠加方法图，然后用叠加方法得出系统的得出系统的Bode图，并由此可以看出各个环节对系统图，并由此可以看出各个环节对系统总特性的影响。总特性的影响。 4.2.2 频率特性频率特性的对数坐标图的对数坐标图 u频率特性对数坐标图由对数幅频特性和对数相频特性图组成。频率特性对数坐标图由对

23、数幅频特性和对数相频特性图组成。u横坐标是以横坐标是以10为底的对数分度，纵坐标则为线性分度。为底的对数分度，纵坐标则为线性分度。u的数值每变化的数值每变化10倍，称为十倍频程，记为倍，称为十倍频程，记为dec。1 、典型环节的、典型环节的Bode图图（1）比例环节）比例环节0)(lg20)(lg20)(jGKjGKjG（2）积分环节）积分环节0)(lg20, 1lg20)(lg2090)(1)(1)(jGjGjGjGjjG（3）微分环节）微分环节0)(lg20, 1lg20)(lg2090)()()(jGjGjGjGjjG（4）惯性环节）惯性环节0)(lg20,lg20lg20)(lg20,

24、0)(lg20,lg20lg20)(lg20/arctan)()()(/111)(2222TTTTTTTTTTTTTjGjGdBjGjGjGjGjjGTjTjG0)(lg20,lg20lg20)(lg20,0)(lg20,lg20lg20)(lg20/arctan)()()(/ 111)(2222TTTTTTTTTTTTTjGjGdBjGjGjGjGjjGTjTjG低频段误差低频段误差 22lg20lg20)(TTe高频段误差高频段误差22lg20lg20)(Te在转折频率处（在转折频率处（ ）误差为）误差为 dBjGeTT3lg20lg20)(lg20)(22T（5）一阶微分环节）一阶微分环

25、节TTTTTTjGjGjjGTjTjGlg20lg20)(lg20/arctan)()(/ 11)(22（6）振荡环节）振荡环节180)(,lg40lg40lg40)(lg20,90)(, 10)(, 0)(lg20,4)1 (lg20)(lg2012arctan)(4)1 (1)(2)1 (1)(/2)(2)(2222222222222222jGjGjGjGjGjGjGjGjjGjjGsssGnnnnnnnnnnn180)(,lg40lg40lg40)(lg20,90)(, 10)(, 0)(lg20,4)1 (lg20)(lg2012arctan)(4)1 (1)(2)1 (1)(/2)(

26、2)(2222222222222222jGjGjGjGjGjGjGjGjjGjjGsssGnnnnnnnnnnn在低频段误差在低频段误差22224)1 (lg20),(e在高频段误差在高频段误差22224)1 (lg20lg40),(e（6）振荡环节）振荡环节（7）延时环节）延时环节)(0)(lg201)(sincos)()(jGjGjGjejGesGjsu关于关于对数幅频特性对数幅频特性:u 积分环节积分环节的为过点的为过点(1,0)、斜率为、斜率为-20dB/dec的直线的直线;u 微分环节微分环节的为过点的为过点(1,0)、斜率为、斜率为20dB/dec的直线的直线;u 惯性环节惯性环节

27、的低频渐近线为的低频渐近线为0dB,高频渐近线为始高频渐近线为始u 于点于点(T,0) 、斜率为、斜率为-20dB/dec的直线的直线;u 导前环节导前环节的低频渐近线为的低频渐近线为0dB,高频渐近线为始高频渐近线为始u 于点于点(T,0) 、斜率为、斜率为20dB/dec的直线的直线;u 振荡环节振荡环节的低频渐近线为的低频渐近线为0dB,高频渐近线为始高频渐近线为始u 于点于点(1,0) 、斜率为、斜率为-40dB/dec的直线的直线;u 二阶微分环节二阶微分环节的低频渐近线为的低频渐近线为0dB,高频渐近线为始高频渐近线为始u 于点于点(1,0) 、斜率为、斜率为+40dB/dec的的

28、直线。直线。典型环节的对数频率特性的特点典型环节的对数频率特性的特点:u关于关于对数相频特性对数相频特性:u 积分环节积分环节的为的为-90的水平线的水平线;u 微分环节微分环节的为的为90 的水平线的水平线;u 惯性环节惯性环节的为在的为在0-90内变化的对称于内变化的对称于u 点点(T,-45 )的曲线的曲线;u 导前环节导前环节的为在的为在090内变化的对称于内变化的对称于u 点点(T,45 )的曲线的曲线;u 振荡环节振荡环节的为在的为在0-180内变化的对称于内变化的对称于u 点点(1,-90)的的曲线；曲线；u 二二阶微分环节阶微分环节的为在的为在0+180内变化的对内变化的对u

29、称于点称于点(1,+90)的的曲线。曲线。（1）将系统传递函数转化为若干个标准形式的环节的）将系统传递函数转化为若干个标准形式的环节的传递函数的乘积形式。传递函数的乘积形式。（2）由传递函数求出频率特性。）由传递函数求出频率特性。（3）确定各典型环节的转角频率。）确定各典型环节的转角频率。（4）作出各环节的对数幅频特性的渐近线。）作出各环节的对数幅频特性的渐近线。（5）根据误差修正曲线对渐近线进行修正，得出各环）根据误差修正曲线对渐近线进行修正，得出各环节的对数幅频特性的精确曲线。节的对数幅频特性的精确曲线。2 、绘制系统、绘制系统Bode图的步骤与实例图的步骤与实例njjvmiisTssTK

30、sG11) 1() 1()(u(6)将各环节的对数幅频特性叠加（不包括系统总的增将各环节的对数幅频特性叠加（不包括系统总的增益益K）。）。u(7)将叠加后的曲线垂直移动将叠加后的曲线垂直移动20lgK，得到系统的对数，得到系统的对数幅频特性。幅频特性。u(8)作出各环节的对数相频特性，然后叠加而得到系统作出各环节的对数相频特性，然后叠加而得到系统总的对数相频特性。总的对数相频特性。u(9)有延时环节时，对数幅频特性不变，对数相频特性有延时环节时，对数幅频特性不变，对数相频特性则应加上则应加上 。) 1025. 0)(15 . 2() 15 . 0( 3)(ssssG40025. 0114 .

31、05 . 21125 . 011321TTT)205. 0)(25()5 . 025. 0(24)(ssssG01055. 43lg20lg20dBk一阶微分环节一阶微分环节惯性环节惯性环节惯性环节惯性环节例例解：化为标准形式解：化为标准形式(1)把把G(s)写成标准形式，并求出写成标准形式，并求出G(j);(2)确定各典型环节的转角频率，确定各典型环节的转角频率，并并由小到大由小到大将其顺序标在横轴上将其顺序标在横轴上;(3)计算计算20lgK，在横坐标上找到，在横坐标上找到=1，纵坐标为，纵坐标为20lgK的点；即的点；即: 点点(1, 20lgK)(4)过该点作斜率为过该点作斜率为-20

32、dB/dec的斜线，以后每遇到一个转的斜线，以后每遇到一个转折频率便改变一次斜率折频率便改变一次斜率;(5)必要时对渐近线进行修正。必要时对渐近线进行修正。njjvmiisTssTKsG11) 1() 1()(直接绘制系统对数幅频特性的步骤直接绘制系统对数幅频特性的步骤:) 1025. 0)(15 . 2() 15 . 0( 3)(ssssG25 . 01140025. 0114 . 05 . 211321321TTTTTT0.11105100.01-20dB/dec-5-104.551000.4240-20dB/dec直接画出幅频特性直接画出幅频特性srad /L()/dB2080(0.5)

33、( )(2)(0.052)sG sss比例环节比例环节惯性环节转折频率惯性环节转折频率惯性环节转折频率惯性环节转折频率一阶微分环节转折频率一阶微分环节转折频率例例解：化为标准形式解：化为标准形式10(21)( )(0.51)(0.0251)sG sss10(12 )()(10.5 )(10.025 )jG jjj 1120.5T21400.025T310.52T20lg20lg1020KdB频率特性为频率特性为-20dB/dec20-20dB/dec200.11101000.4240srad /L()/dB比例环节比例环节一阶微分环节转折频率一阶微分环节转折频率惯性环节惯性环节转折频率转折频率

34、惯性环节惯性环节转折频率转折频率解：化为标准形式解：化为标准形式10(0.21)( )(51)(0.021)sG sss1150.2T210.25T31500.02T20lg20lg1020KdB频率特性为频率特性为10( 0.21)( )( 51)( 0.021)jG sjj)50)(2 . 0(55)(sssssG）（现将积分环节和现将积分环节和比例环节在比例环节在=1处叠加，然后再处叠加，然后再根据不同的转折根据不同的转折频率进行叠加。频率进行叠加。10-210-1100101102103-180-150-120-90Phase (deg)Bode DiagramFrequency (r

35、ad/s)-100-50050System: sysFrequency (rad/s): 0.198Magnitude (dB): 19System: sysFrequency (rad/s): 5Magnitude (dB): -31System: sysFrequency (rad/s): 49.6Magnitude (dB): -56.8Magnitude (dB)Step ResponseTime (seconds)Amplitude012345600.050.10.150.20.250.30.35System: sysTime (seconds): 1.34Amplitude: 0.

36、249System: sysSettling time (seconds): 4.15System: sysPeak amplitude: 0.29Overshoot (%): 15.9At time (seconds): 1.93System: sysFinal value: 0.25)42)(10)(40(400)(2sssssG10-1100101102-360-270-180-900Phase (deg)Bode DiagramFrequency (rad/s)-120-100-80-60-40-200System: sysFrequency (rad/s): 2Magnitude (

37、dB): -12.3System: sysFrequency (rad/s): 10.1Magnitude (dB): -43.3System: sysFrequency (rad/s): 40.2Magnitude (dB): -79.5Magnitude (dB)10010)(110)(2(400)(2sssssGStep ResponseTime (seconds)Amplitude010203040506000.20.40.60.811.21.41.61.82System: sysSettling time (seconds): 39.7System: sysFinal value:

38、210-210-1100101102-360-270-180-900Phase (deg)Bode DiagramFrequency (rad/s)-100-80-60-40-20020System: G1Frequency (rad/s): 0.1Magnitude (dB): 2.99System: G1Frequency (rad/s): 1.99Magnitude (dB): -22.8System: G1Frequency (rad/s): 9.99Magnitude (dB): -48.2Magnitude (dB)4.3 频率特性的特征量频率特性的特征量u 零频幅值零频幅值 u

39、复现频率复现频率 与复现带宽与复现带宽 u 谐振频率谐振频率 及相对谐振峰值及相对谐振峰值u 截止频率截止频率 和截止带宽和截止带宽带宽越大，响应的快速性越好，即过渡过程时间越短。带宽越大，响应的快速性越好，即过渡过程时间越短。)0(AMM0r)0(/(maxAAMrbb0 例例1 )5)(20(300)(jjjjGK2323223225300100arctan)()100()25300(/300)()100(25300300300)5)(20(300)(BBBAjjjjjG)5)(20(300)(ssssGK 解：频率特性为解：频率特性为闭环频率特性闭环频率特性闭环幅频特性闭环幅频特性闭环相

40、频特性闭环相频特性u 零频幅值零频幅值u 谐振频率谐振频率 及相对谐振峰值及相对谐振峰值u 截止频率截止频率1)0(A48. 2r76. 0rM5 . 4b4.4 最小相位系统最小相位系统1 最小相位传递函数与最小相位系统最小相位传递函数与最小相位系统 在复平面在复平面s右半面上没有极点和零点的传右半面上没有极点和零点的传递函数称为最小相位传递函数；具有最小相位递函数称为最小相位传递函数；具有最小相位传递函数的系统称为传递函数的系统称为最小相位系统最小相位系统。2 产生非最小相位的一些环节产生非最小相位的一些环节 (1)延时环节延时环节 (2)不稳定的导前环节和二阶微分环节不稳定的导前环节和二

41、阶微分环节 (3)不稳定的惯性环节不稳定的惯性环节 n一个系统如果它的开环传递函数的全部零极点都位于一个系统如果它的开环传递函数的全部零极点都位于S平面平面的左半平面或虚轴上，则称此系统为最小相位系统。的左半平面或虚轴上，则称此系统为最小相位系统。n幅频特性相同的系统中最小相位系统的相位变化最小。幅频特性相同的系统中最小相位系统的相位变化最小。n幅频特性确定后，其对应的最小相位系统是唯一的。幅频特性确定后，其对应的最小相位系统是唯一的。最小相位系统最小相位系统非最小相位系统非最小相位系统 sesTsTsGsTsTsGsTsTsGsTsTsG11)(411)(311)(211)(11204120312021201例例T110T2（1）当某当某 处的对数幅频特性渐近线的斜率发生变化时，此处的对数幅频特性渐近线的斜率发生变化时，此 即即为某个环节的转折频率。为某个环节的转折频率。 当斜率变化当斜率变化+20dB/dec时时,可知可知 处有一个处有一个一阶微分环节一阶微分环节