清华大学版理论力学课后习题答案大全动量矩定理及其应用

1、第9章动量矩定理及其应用9- 1计算下列情形下系统的动量矩。1 .圆盘以 的角速度绕 。轴转动，质量为 m的小球M可沿圆盘的径向凹槽运动，图示瞬时 小球以相对于圆盘的速度vr运动到OM = s处（图a）;求小球对 O点的动量矩。2 .图示质量为 m的偏心轮在水平面上作平面运动。轮心为A,质心为 C,且AC = e；轮子半径为R,对轮心 A的转动惯量为Ja；C、A、B三点在同一铅垂线上（图b）。（1）当轮子只滚不滑子的动量和对 B点的动量矩。解：1、LO =mcos2 （逆）2、（1）p = mvc = m（vA，e）二Lb =m%（R e） Jc . =mvA习题9 1图VA、 3已知，求轮(

2、b)时，若Va已知，求轮子的动量和对B点的动量矩；（2）当轮子又滚又滑时，若(2) p =mvC =m(vA +切 e)2、LB =mvC(R e) Jc . =m(vA，e)(R e) - (Ja -me ) - -m(R e)vA - (Ja - meR) .习题9- 2图92图示系统中，已知鼓轮以3的角速度绕O轴转动，其大、小半径分别为R、r,对O轴的转动惯量为 Jo;物块A、B的质量分别为 mA和mB；试求系统对 O轴的动量矩。 解：22、Lo =（Jo mAR mBr ） 9 3图示匀质细杆OA和EC的质量分别为50kg和100kg,并在点A焊成一体。若此结构在图示位 置由静止状态释

3、放，计算刚释放时，杆的角加速度及较链O处的约束力。不计较链摩擦。习题20-3解图解：令 m = moA = 50 kg ,则 mEc = 2m 质心D位置：(设l = 1 m),“5,5d = OD = l = m66刚体作定轴转动，初瞬时w =0Jo 二=mg 2 2mg lJo J ml2 ' 2m (2l )2 2ml2 =3ml2 312即 3ml2 ：-mgl52:g =8.17r ad / s6lt _5, _ _25 aD l g636由质心运动定理：3m aD = 3mg - F°y一 八 八2511FOv =3mg -3mg = mg =449Ny36129

4、4卷扬机机构如图所示。可绕固定轴转动的轮B、C,其半径分别为R和r,对自身转轴的转动惯量分别为 Ji和J2。被提升重物 速度。解：对轮C:A的质量为 m,作用于轮C的主动转矩为M,求重物 A的加J2: C =M -FTr对轮B和重物A:2、(J1 mR )：- - FTR - mgR 运动学关系：2c (M -mgr)rR a =2ZT2-2-2J1r2 J2R2 mR2r2题9-4解图9-5图示电动绞车提升一质量为动力偶。已知主动轴和从动轴连同安装在这两轴上的齿轮以及其它附属零 件对各自转动轴的转动惯量分别为和J2;传动比 上：ri = i；吊索缠绕在鼓轮上，此轮半径为Ro设轴承的摩擦和吊索

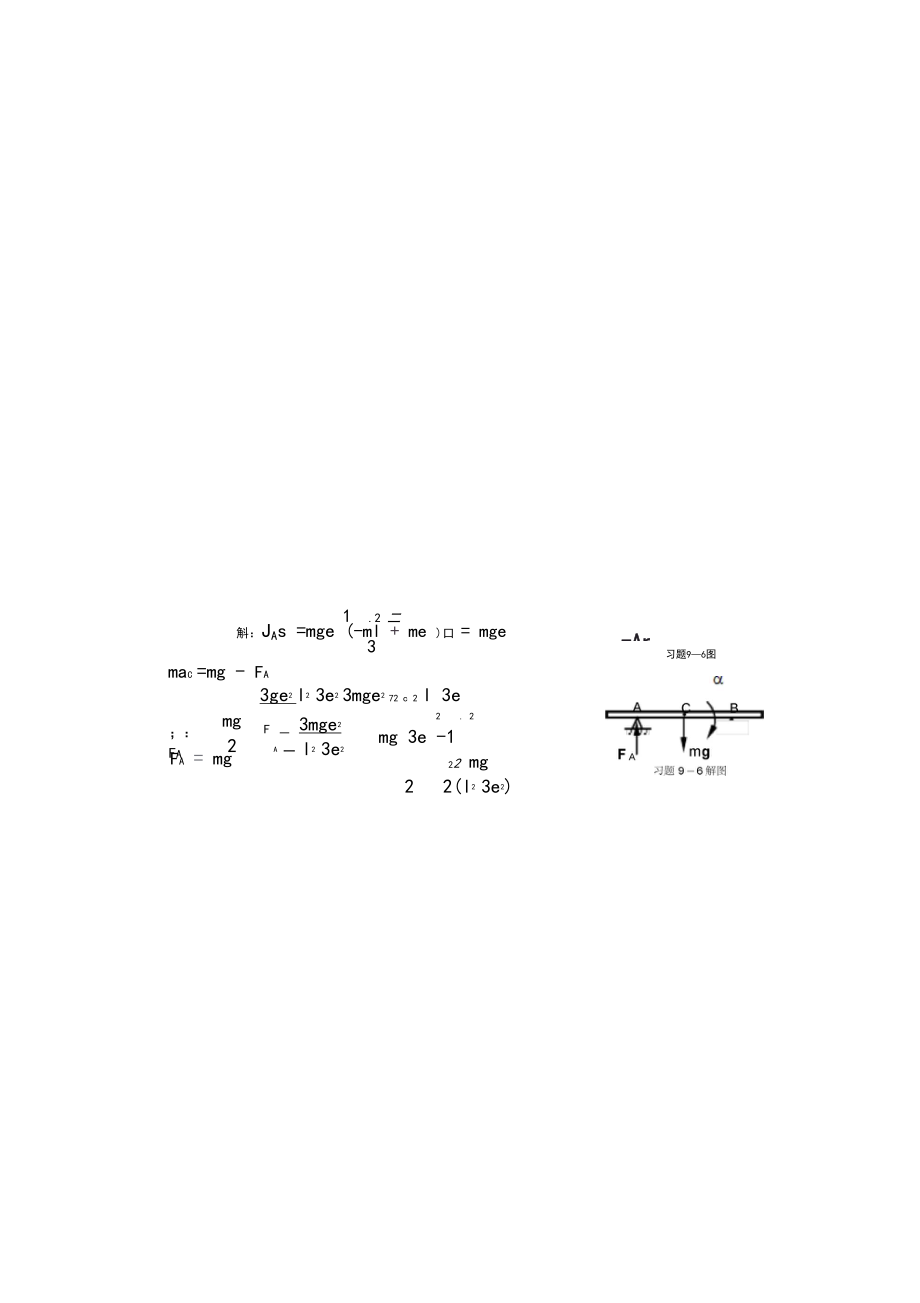
5、的质量忽略不计，求重物的 加速度。解：对轮1 （图a）:Jr1 =M -Fr1对轮2 （图b）：2、（J2 mR ）： 2 = F r2 -mgRm的物体，在其主动轴上作用一矩为J2 I习题9 5图M的主 | F N11% = r2a2 ； % = i a2_ Mi -mgR'2 " J2 mR2 J1i2重物的加速度：a = r： 2 = (Mi _m2gR)R2J2 mR J1i96均质细杆长 的距离相等，即 AC = 量 AF a°2l ,质量为 m,放在两个支承CB = e。现在突然移去支承A和B上,如图所示。杆的质心c到两支承B,求在刚移去支承B瞬时支承

6、A上压力的改变-ArFa = mg -习题96图1.2 二斛：JAs =mge (-ml + me )口 = mge3maC =mg - Fa3ge2 l2 3e2 3mge2 72 c 2 l 3e；：Famg2F _ 3mge2A 一 l2 3e22. 2mg 3e -122 mg22(l2 3e2)9-7为了求得连杆的转动惯量，用一细圆杆穿过十字头销A处的衬套管，并使连杆绕这细杆的水平轴线摆动，如图a、b所示。摆动100次所用的时间为100s。另外，如图c所示，为了求得连杆重心到悬挂 轴的距离AC = d,将连杆水平放置，在点 A处用杆悬挂，点B放置于台秤上，台秤的读数 F = 490N

7、。已知 连杆质量为80kg, A与B间的距离l=1m,十字头销的半径r = 40mm。试求连杆对于通过质心 C并垂直于 图面的轴的转动惯量 Jc。解：“图(a), e超时,Jai - -mg(d，r)iJa? mg(d 叶)？ -0 .mg(d)=0Jamg(d r)n =一1T=2 无 I JA( 1)- n , mg(d r)Ja =Jc +m(d +r)2( 2)由图(b):一. Fl 5Z M a =0 , d =_ =。625 m mg 8代入(1)、(2),注意到周期T=2s,得, mg(d ' r) 、2gJc =2_m -m(d r) =m(d r)- -(d r)正冗

8、_9 8_=80 0.665 (98 -0.665)冗2=17.45kg m98图示圆柱体A的质量为m,在其中部绕以细绳, 其初速为零。求当圆柱体的轴降落了高度 h时圆柱体中心 力Ft。解：法1 ：图（a）maA =mg FtJa“ =FTraA 二 r a,12J a =mr21斛得FT =7 mg （拉）3绳的一端B固定。圆柱体沿绳子解开的而降落A的速度u和绳子的拉(1)(2)(3)习题9 8图aA2. 一=7g (常重)3(4)由运动学 VA=K=23'gK (J)3法2:由于动瞬心与轮的质心距离保持不变, 量矩定理：Jc =mgr.232Jc =Ja »mr =-mr

9、2故可对瞬心C用动(5)再由一r2aA =. g (向式(4)3maA =mg -FT1,、FT =mg (拉)32 Va =12aAhJ3gh ( J )3(a)99鼓轮如图，其外、内半径分别为 =R T,鼓轮在拉力 F的作用下沿倾角为 试求质心O的加速度。R和r,质量为 m,对质心轴 O的回转半径为9的斜面往上纯滚动,解：鼓轮作平面运动，轴 O沿斜面作直线运动: maO = F - Ff - mg s i n纯滚：aO代入(2)"" Fr FfR二R：p, J!(3)F力与斜面平行，不计滚动摩阻。Fm ；2 aO - Fr Ff RR解(1)、(4)联立，消去Ff,得F

10、R(R r) -mg Rs i nm(R2 ：2)(4)习题9 9图题9-9解图1 Ff9RO9-10图示重物A的质量为m,当其下降时，借无重且不可伸长的绳使滚子C沿水平轨道滚动而不滑动。绳子跨过不计质量的定滑轮D并绕在滑轮B上。滑轮B与滚子C固结为一体。已知滑轮 B的半径为R,滚子C的半径为r,二者总质量为 m',其对与图面垂直的轴 O的回转半径为 P。求：重物A的加 速度。习题9- 10图解：法1:对轮:J。：. =TRFr mao =F _T 对A:maA =mgT又：aA =Hh绳以o为基点：t =aHa n a ta HO aHOaH =aHO -ao =Ra -ret =(

11、R -r)ct (一)aAR -r)a ( J )由上四式联立，得(注意到 J。田行)2mg(R _r)ga A -m ( :'2 ;r2) N；m(R _r)2 - m ' ( ; ：；r2) m ("R _ip"(a)法2:对瞬心E用动量矩定理（本题质心瞬心之距离为常数）Je? =T（R _r）maA =mg -T又 aA -(R _r)：-J E =JO +m r2 =m '(炉 +r2)可解得：a a =2gl一m.(2 r2) 11Im (Rr)2a o o ona Ha Hot H a Ha HO(b)半径为r,在力偶作用下沿水平面作纯滚

12、动。若力偶的力偶矩 M为O的加速度及其与地面的静滑动摩擦力。(1)习题9 11图911 图示匀质圆柱体质量为 m, 常数，滚动阻碍系数为 5,求圆柱中心解：Jd ： =M -MfMf = FnFn =mg ,32Jd -mr2D 2 a Ct r代入（1）,得2（M 、mg） a -3mr又：ma =FF =2(M _、mg)_3r9-12跨过定?t轮 D的细绳，一端缠绕在均质圆柱体A上，另一端系在光滑水平面上的物体B上，如图所示。已知圆柱 A的半径为r,质量为 m1；物块B的质量为 m2。试求物块 B和圆柱质 心C的加速度以及绳索的拉力。滑轮 D和细绳的质量以及轴承摩擦忽略不计。解：对轮 C

13、： Jca =FTrmac -mig - Ft对物块B： m2aB =Ft口11且：ac =aB +ra ； jc =3m1r解得：aB-g ； m1 3m2acm12m习题9- 12图m1 3mFtmm2g m1 3m29-13图示匀质圆轮的质量为 m,半径为r,静止地放置在水平胶带上。若在胶带上作用拉力 F,并 使胶带与轮子间产生相对滑动。设轮子和胶带间的动滑动摩擦因数为 f。试求轮子中心。经过距离s所需的 时间和此时轮子的角速度。解：图（a）,轮O平面运动:(1)(2)(3)(4)(5)(6)习题9 13图maO = F10 =Fn mgJo =Fr由(2),Fn =mg动滑动时，Fi

14、=fFN =fmg(4)代入(1),得ao =fg(4)代入(3),得(JO =!mr2)2r由（5）代入下式:1.2s = aOt 2得 t = 2sfg2914图示匀质细杆去不计，试求杆的初始角加速度。AB质量为m,长为l,在图示位置由静止开始运动。若水平和铅垂面的摩擦均略8 =a =1 J2 fgs (逆) r解：法1: P为AB杆瞬心，pc=1 图(a)：2J p ：. =mg l-sin ,口2,1.2J P =-ml33g .,、二 ct=-sin 日(1)2l法2: AB杆平面运动mxC F B(2)myC =Fa-mg(3)JcO(=Fa - sin0-Fb -cosQ(4)2

15、2l .l .xc =-sin 0 , yc =一 cost? 22l . /-l(b)xC =cos 日 8 , yC =一sin 6 6 22-ll . l , /xc =一sin9 斤 +-cosH 3 =cosH 0(5)222l .二 l . l .yC =cos8 孑sin日 8=sin 8 8(6)222(初瞬时6=0)(7)(8)0 =a将（5）、（6）、（7）代入（2）、（3）、（4）得m cos t1 : 一 Fb2一:msin 二：-FA -mg ml212-： = FA sin 二-FB cosi(9)(10)解得：*可，与（1）式相同。915圆轮A的半径为 R,与其固

16、连的轮轴半径为r,两者的重力共为W,对质心 C的回转半径为R缠绕在轮轴上的软绳水平地固定于点D。均质平板 BE的重力为 Q,可在光滑水平面上滑动，板与圆轮间无相对滑动。若在平板上作用一水平力F,试求平板 BE的加速度。习题9 15图习题9- 15解图解：对轮 C： JC« =Ff R FTr ； JC =WP2 gW caC - FT _ Ff ； 3c - r -g对板BE:QaBE = F - Ff ； aBE = ( R - r ) / g求得:3be 二F(R-r)2g2-.22Q(R -r) W(； r )*9 16图示水枪中水平管长为 21,横截面面积为 A,可绕铅直轴z

17、转动。水从铅直管流入，以相对速度u从水平管喷出。设水的密度为P,解：水平管上各点科氏加速度相同a c =2 3 vac =2cov科氏惯性力均布，其合力（如图）：Fic = P lA ac =2;二Vr i lAM z =2 FIC - =2 P 1% vr2试求水枪的角速度为 与时，流体作用在水枪上的转矩 M z o(a)*9-17图示匀质细长杆 AB,质量为m,长度为I,在铅垂位置由静止释放，借A端的水滑轮沿倾斜角为e的轨道滑下。不计摩擦和小滑轮的质量，试求刚释放时点a的加速度。解：图（a）,初瞬时0AB =0,以A为基点，则aC =aCx ' aCy =aA ' aCA即

18、 acx =3a acA cos6 =3a ctcos62acy = cca sin 1 sin 二(1)(2)习题9-17图由平面运动微分方程:maCx =mg sin ?aCx =gs*maCy =mg cos 71 -FnJc - Fn -sin 12(3)(4)12BP ml 二,二Fn12l .一 Sin r2-(5)解(2)、(4)、联立得"rSy(6)由(1)、(3),(6)代入，得得 aA cos? :. - gsin 1 2_ 4sin ? 八aA g1 3 sin 1D棱是光滑的。在图*9 18匀质细长杆AB,质量为m, 示位置将杆突然释放，试求刚释放时，质心解：

19、初始静止，杆开始运动瞬时，长为l, CD = d,与铅垂墙间的夹角为 日, C的加速度和D处的约束力。切向，即沿 AB方向，所以aD此时沿(a),以D为基点：由 aCx . aCy = aD ' aCD . a CDaCx -Cd =d ： 1由AB作平面运动：maCx =mgsin ? -FnVD必沿支承处AB方向，如图(1)习题9 18图maCy =mgcos:-1 .12ml .1 =Fzd 12(3) , aCy =gsc a(1)、(2)、(4)联立(2)(3)来,acx2.12gd sin 口22l 12d一 12 一 mgl sin J.l2 12d2(a)919如图所示

20、，足球重力的大小为4.45N,以大小 =6.1m/s,方向与水平线夹形成头球。球员以头击球后，球的速度大小为v；=9.14m/s,并与水平线夹角为时间为0.15s。试求足球作用在运动员头上的平均力的大小与方向。解：击球前后球的动量改变为5 mm(v； -v1)4 45p =4459.14cos20o -(-6.1cos40o),-9.14sin20o -(-6.1sin40o) g=0.454 (13.26,0.795) = (6.02,0.361) N s设pp与水平夹角a二 J加 十%y =6.03 N -p6.03=40.2 NP(a)-'Py0.361一 二 tan - 0.06Px6.02二二3.431°习题9- 19图40 0角的速度向球员飞20 0角。若球头碰撞t 0.15人头受力F与 即反向，即向左下方。(b)9-20边长为a的方形木箱在无摩擦的地板上滑动，并与一小障碍A相碰撞。碰撞后绕 A翻转。试求木箱能完成上述运动的最小初速 V。；木箱碰撞后其质心的瞬时速度 vc与瞬时角速度Oo解：碰前方箱以初速度 v0平移，碰后箱绕(a)A点转动直到翻倒,(b)碰撞中箱只在 A点受冲量，重力等其它有限力的冲量可忽略不计，因此碰撞前后箱对 设箱的质量为mA点的