直角三角形全等的判定公开课_第1页
直角三角形全等的判定公开课_第2页
直角三角形全等的判定公开课_第3页
直角三角形全等的判定公开课_第4页
直角三角形全等的判定公开课_第5页
已阅读5页，还剩7页未读， 继续免费阅读

下载本文档

版权说明：本文档由用户提供并上传，收益归属内容提供方，若内容存在侵权，请进行举报或认领

文档简介

3.5.2

直角三角形全等的判定

(第一课时）授课人：颜向阳忆一忆前面我们学习了哪些判定两个三角形全等的方法？

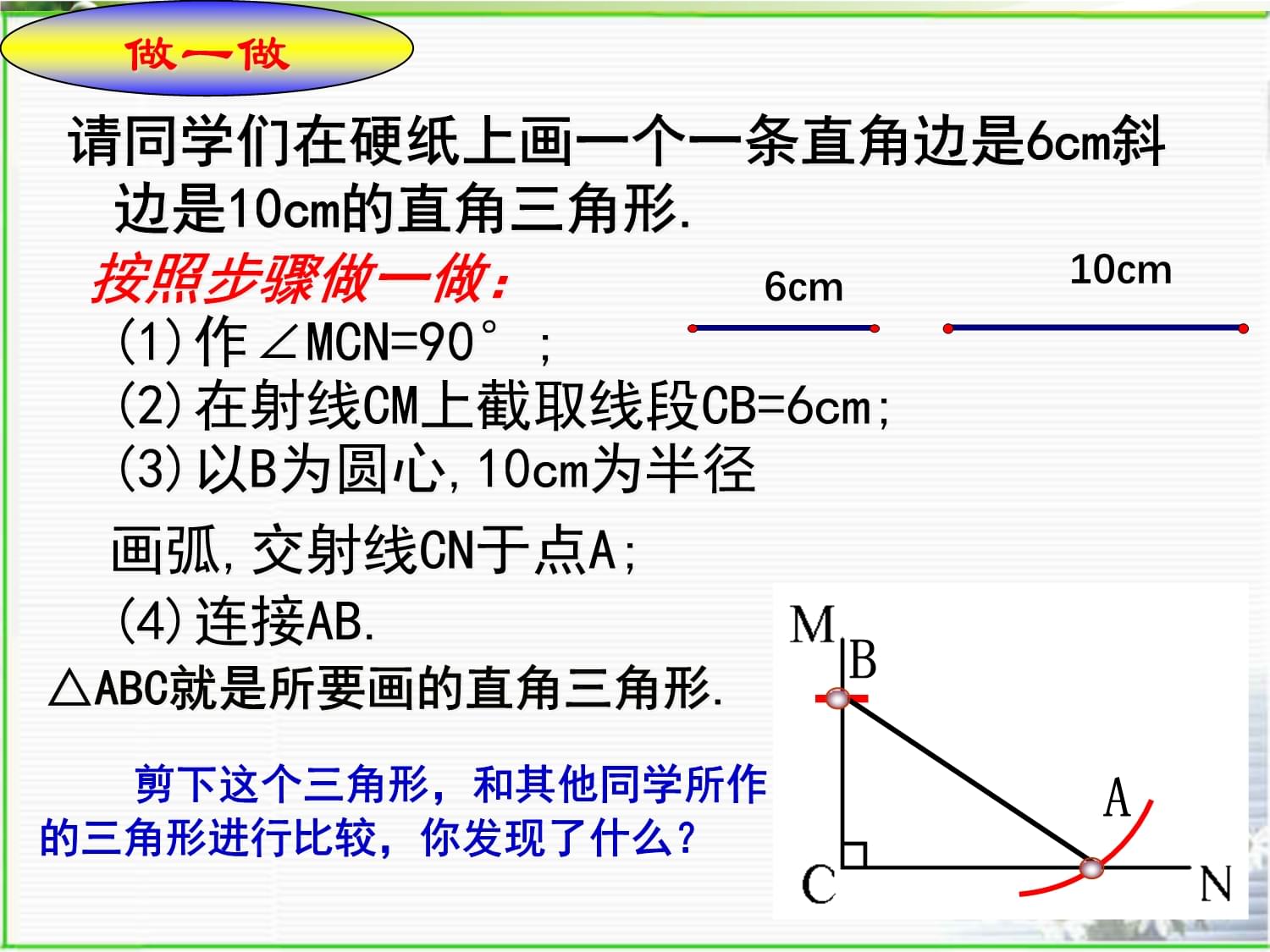
SASASAAASSSS做一做请同学们在硬纸上画一个一条直角边是6cm斜边是10cm的直角三角形.按照步骤做一做：(1)作∠MCN=90°;(2)在射线CM上截取线段CB=6cm;(3)以B为圆心,10cm为半径画弧,交射线CN于点A;(4)连接AB.BA△ABC就是所要画的直角三角形.6cm10cm

剪下这个三角形，和其他同学所作的三角形进行比较，你发现了什么？如图在ΔABC和ΔA/B/C/中，∠C=∠C/=90o,AB=A/B/，AC=A/C/

说明ΔABC和ΔA/B/C/

全等的理由。解:∵∠C=∠C/

=90°∴B、C、B/在同一直线上，AC┴BB/∵AB=A/B/∴BC=B/C/（等腰三角形三线合一）∵AC=A/

C/

（公共边）∴RtΔABC≌RtΔA/B/C/（SSS）小组合作说明这个结论的正确性CBAB/A/C/

斜边和一条直角边对应相等的两个直角三角形全等.简写：“斜边、直角边”或“HL”AB=A´B´AC=A´C´（或BC=B´C´）∴Rt△ABC≌Rt△A´B´C´(HL)直角三角形全等的判定方法∵获得新知在Rt△ABC和Rt△A´B´C´中判断直角三角形全等条件三边对应相等SSS一锐角和它的邻边对应相等ASA一锐角和它的对边对应相等AAS两直角边对应相等SAS斜边和一条直角边对应相等HL

直角三角形是特殊的三角形，所以不仅有一般三角形判定全等的方法，还有直角三角形特有的判定方法“HL”.

我们应根据具体问题的实际情况选择判断两个直角三角形全等的方法.想一想你能够用几种方法说明两个直角三角形全等？例题1.如图，AC=AD，∠C，∠D是直角，将上述条件标注在图中，你能说明BC与BD相等吗？解：BC=BD

∵在Rt△ACB和Rt△ADB中

AB=AB,AC=AD.∴Rt△ACB≌Rt△ADB(HL).∴BC=BD(全等三角形对应边相等).CDAB你还能得出什么结论？

1.如图，两根长度为12米的绳子，一端系在旗杆上，另一端分别固定在地面两个木桩上，两个木桩离旗杆底部的距离相等吗？请说明你的理由。∵AB=AC（已知）AD=AD（公共边）∴Rt△ABD≌Rt△ACD(HL)∴BD=CD解：BD=CD∵∠ADB=∠ADC=90°学以致用1.已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF.试说明:

△ABC是等腰三角形.分析:要说明△ABC是等腰三角形,就需要说明AB=AC;进而需要说明∠B=∠C所在的△BDF≌△CDE;而△BDF≌△CDE的条件:从而需要说明∠B=∠C;BD=CD,DF=DE均为已知.因此,可得△ABC是等腰三角形.DBCAFE请将解题过程规范化书写出来.练一练通过这节课的学习你

人人文库> 全部分类> 教育资料 > 课件下载

温馨提示

  • 1. 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
  • 2. 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
  • 3. 本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
  • 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
  • 5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
  • 6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
  • 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

最新文档

评论

0/150

提交评论