高等数学1-6闭区间上连续函数的性质_第1页
高等数学1-6闭区间上连续函数的性质_第2页
高等数学1-6闭区间上连续函数的性质_第3页
高等数学1-6闭区间上连续函数的性质_第4页
高等数学1-6闭区间上连续函数的性质_第5页
已阅读5页，还剩9页未读， 继续免费阅读

下载本文档

版权说明：本文档由用户提供并上传，收益归属内容提供方，若内容存在侵权，请进行举报或认领

文档简介

一、最值定理二、介值定理

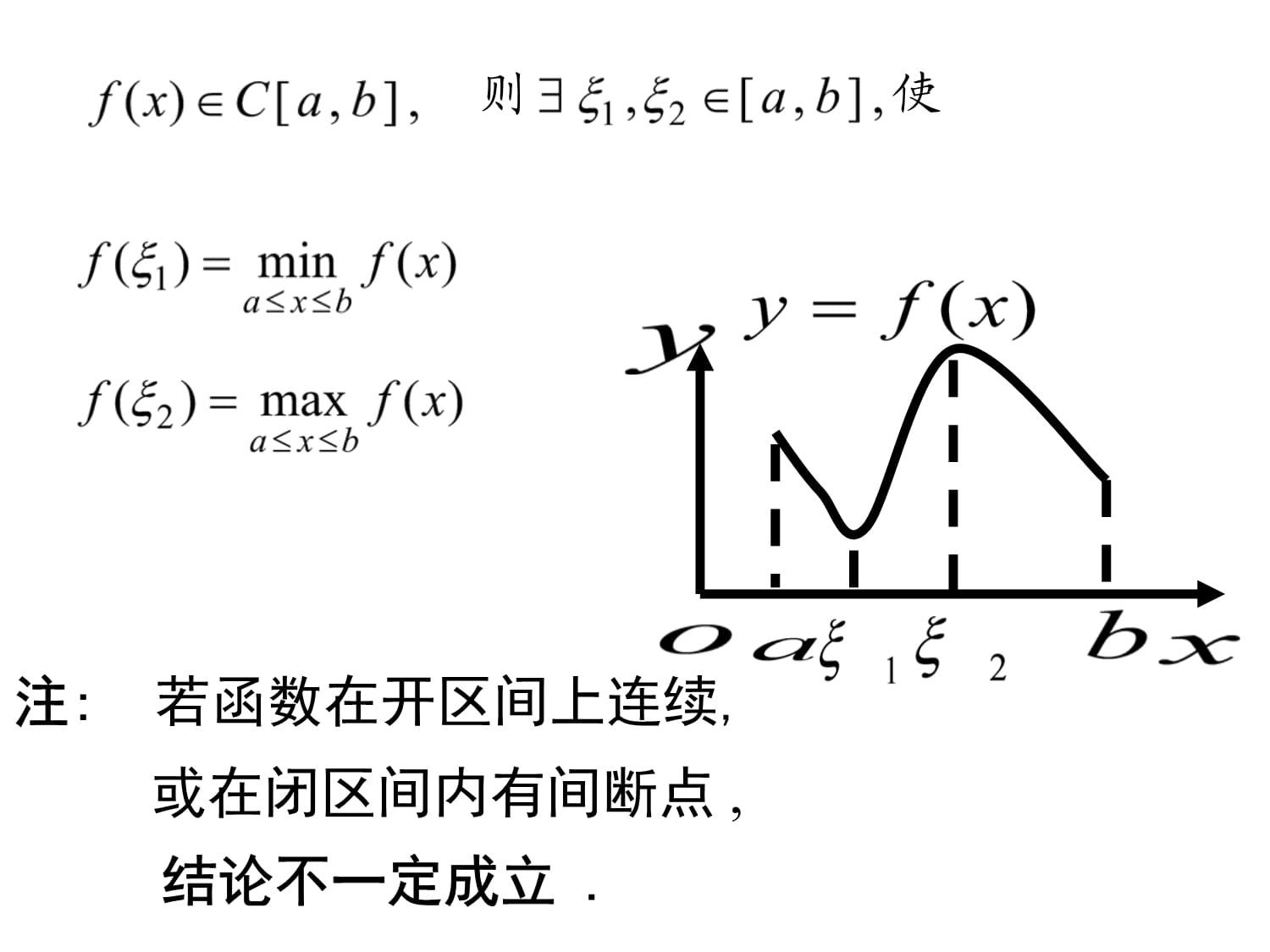
第一章第十节闭区间上连续函数的性质一、最值定理定理1.在闭区间上连续的函数在该区间上即:设则使一定有最大值和最小值.注:

若函数在开区间上连续,结论不一定成立.则使或在闭区间内有间断点

,例如,无最大值和最小值也无最大值和最小值又如,

推论.

由定理1可知有证:

设上有界.在闭区间上连续的函数在该区间上有界.二、介值定理定理2.

(零点定理)至少有一点且使定理3.(介值定理)设且则对A

与B

之间的任一数C,使至少有一点证:

作辅助函数则且故由零点定理知,至少有一点使即推论:在闭区间上的连续函数必取得介于最小值与最大值之间的任何值.例1.证明方程证:显然又故据零点定理,至少存在一点使即在区间内至少有一个根.例1.证明方程一个根.说明:内必有方程的根;取的中点内必有方程的根;可用此法求近似根.二分法在区间内至少有则则上连续,且恒为正,例2.

设在对任意的必存在一点证:使令,则使故由零点定理知,存在即当时,取或,则有证明:在上达到最大值与最小值;上可取最大与最小值之间的任何值;4.当时,使必存在上有界;在在则设)(.1xf],[ba)(.2xf],[ba)(.3xf],[ba0)()(<bfaf.0)(=xf,),(baÎx小结则证明至少存在使提示:

令则易证1.

设一点,]2,0[)(aCxfÎ,)2()0(aff=,],0[aÎx.)()(aff+=xx,)()()(xfaxfx-+=j,],0[)(aCxÎj0)()0(£ajj备用题

至少有一个不超过4的证：证明令且根据零点定理,原命题得证.内至少存在一点在开区间显然正根.1)(3--=-xexxf[],4,0)(上连续在闭区间xf=)0(f13---e1434---e=

人人文库> 全部分类> 教育资料 > 课件下载

温馨提示

  • 1. 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
  • 2. 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
  • 3. 本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
  • 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
  • 5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
  • 6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
  • 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

最新文档

评论

0/150

提交评论