机械制图直线的投影课件

直线的投影

两点确定一条直线，将两点的同面投影用直线连接，就得到直线的同面投影(粗实线2b,b细线宽)。

直线对一个投影面的投影特性一、直线的投影特性AB●●●●ab直线垂直于投影面投影重合为一点积聚性直线平行于投影面投影反映线段实长实形性ab=AB直线倾斜于投影面投影比空间线段短类似性ab=Abcosα●●AB●●abαAMB●a≡b≡m●●●aaabbb●●●●●●直线的投影两点确定一条直线，将两点的同面投影用直二、各种位置直线的投影特性（三大类七种）投影面平行线平行于某一投影面而与其余两投影面倾斜投影面垂直线水平线（平行于Ｈ面）正平线（平行于Ｖ面）侧平线（平行于Ｗ面）铅垂线（垂直于Ｈ面）正垂线（垂直于Ｖ面）侧垂线（垂直于Ｗ面）一般位置直线与三个投影面都倾斜的直线统称特殊位置直线（注意两者区别）垂直于某一投影面而与其余两投影面平行二、各种位置直线的投影特性（三大类七种）投影面平行线平行于

如图,直线AB与三个投影面都倾斜。V面投影a’b’,H面投影ab,W面投影a”b”。

设直线段AB对H、V、W三个投影面的倾角分别为α、β、γ，则ab=ABcosα,a’b’=ABcosβ,a”b”=ABcosγ.三个投影都具有类似性.投影特征：三斜无实长投影特性：1.三个投影长度都缩短，且与投影轴倾斜；2.其投影与投影轴的夹角，不反映直线对投影面的倾角。VHW

αβγ1.一般位置直线baabba

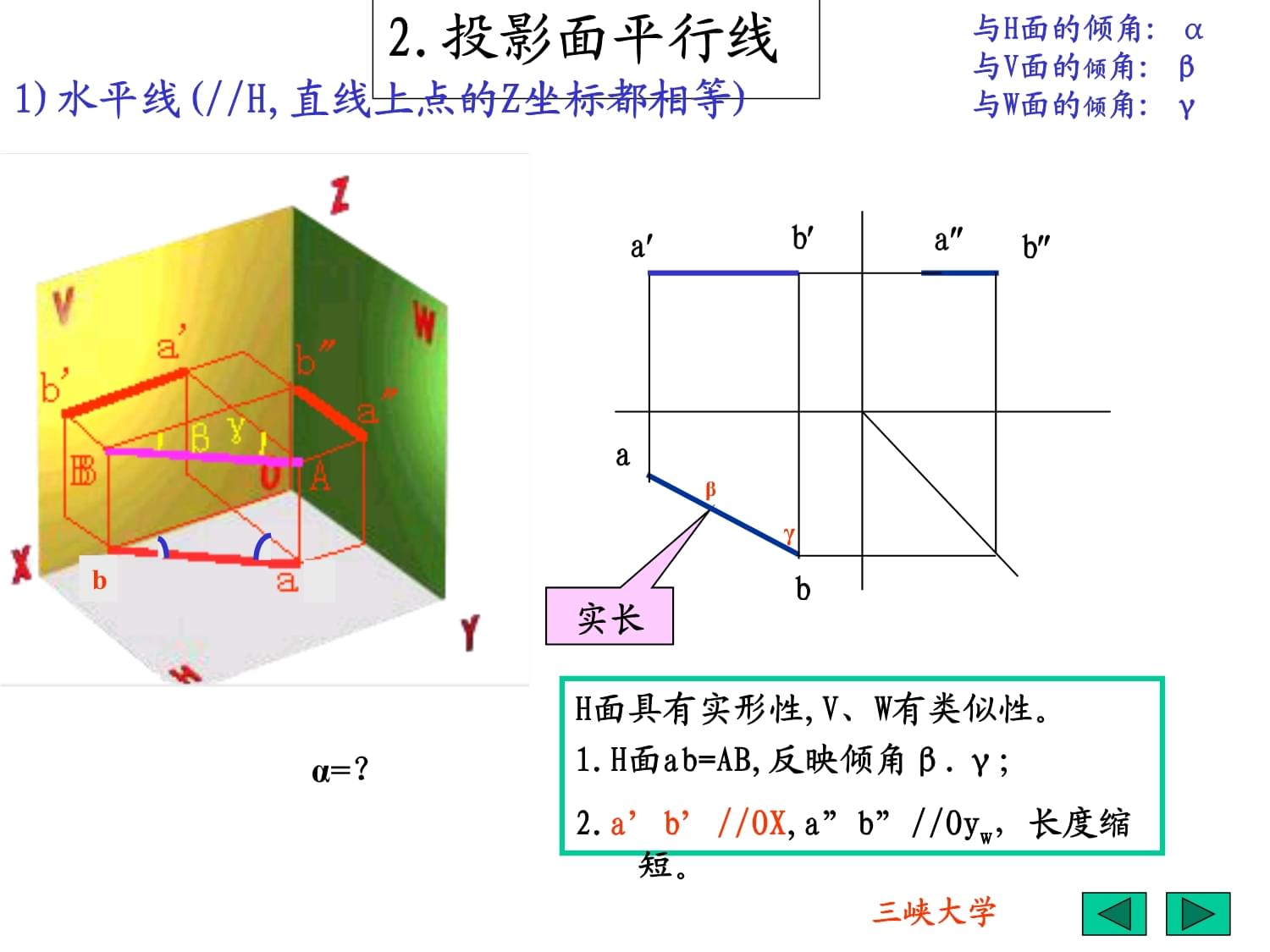
ABaa’’b’’a’b’b如图,直线AB与三个投影面都倾斜。V面投影a’b’2.投影面平行线与H面的倾角:α与V面的倾角:β与W面的倾角:γH面具有实形性,V、W有类似性。1.H面ab=AB,反映倾角β.γ；2.a’b’//OX,a”b”//Oyw，长度缩短。b1)水平线(//H,直线上点的Z坐标都相等)实长βγbaaabbα=？2.投影面平行线与H面的倾角:αH面具有实形性,V、W有V面具有实形性,H、W有类似性.

1.V面a’b’=AB,反映倾角α.γ；2.ab//OX,a”b”//OZ，长度缩短。baabab2)正平线（//V,所有点的Y坐标相等）γ实长αV面具有实形性,H、W有类似性.baabab2)正平baabba①

在其平行的那个投影面上的投影反映实长，并反映直线与另两投影面倾角的大小。②另两个投影面上的投影平行于相应的投影轴。3)侧平线（//W,所有点X坐标相等）投影特性：实长αβ投影特征：一斜两平行W面具有实形性,H、V有类似性.

1.W面a”b”=AB,反映倾角α.β；2.a’b’//OZ,ab//OYH，长度缩短。baabba①在其平行的那个投影面上的投影反映实长1.ab积聚成一点；2.a’b’⊥OX,a”b”⊥OYw,都反映实长。3.投影面垂直线1)铅垂线（⊥H面,所有点的X.Y相等）●aba(b)ab问α、β、γ？1.ab积聚成一点；3.投影面垂直线1)铅垂线（⊥H面,所有1.a’b’积聚成一点;2.ab⊥OX,a”b”⊥OZ,都反映实长。2)正垂线（⊥V面,所有点的X.Z相等）●a(b)abba1.a’b’积聚成一点;2)正垂线（⊥V面,所有点的X.Z3)侧垂线（⊥W面,Y和Z相等）②另外两个投影，反映线段实长，且垂直于相应的投影轴。①在其垂直的投影面上，积聚为一点。投影特性:●ababa(b)投影特征：一点两垂直1.a”b”积聚成一点；2.ab⊥OYH,a’b’⊥OZ,都反映实长。3)侧垂线（⊥W面,Y和Z相等）②另外两个投影，反映线段实直线上的点具有两个特性：1.从属性若点在直线上，则点的各个投影必在直线的各同面投影上。利用这一特性可以在直线上找点，或判断已知点是否在直线上。ABbbaaXOccCc三、直线与点的相对位置2.定比性直线上的点,分线段之比在投影中不变。即AC:

CB=ac:

cb=ac:

cb=ac

:

cb直线上的点具有两个特性：ABbbaaXOccCc三、点C不在直线AB上例1：判断点C是否在线段AB上。abcabc①c②abcab●点C在直线AB上根据点的从属性，若点的投影有一个不在直线的同名投影上，则该点必不在此直线上。对于一般位置直线两个投影就可以判断了。●●●点C不在直线AB上例1：判断点C是否在线段AB上。abca例2：判断点K是否在线段AB上。ab●k因k不在a

b上，故点K不在AB上。方法二：应用定比性abkabk●●方法一：应用从属性●●例2：判断点K是否在线段AB上。ab●k因k不在a例3已知点C在线段AB上，求点C的正面投影。bXaabccaccbXOABbbaacCcHV应用定比性（相似△）求例3已知点C在线段AB上，求点C的正面投影。bXa四、空间两直线的相对位置分为：平行、相交、交叉⒈两直线平行投影特性：

平行性——空间两直线平行，则其各同面投影必相互平行，反之亦然。aVHcbcdABCDbda等比性——空间两线段平行，其长度之比等于同面投影长度之比。⒈两直线平行

即：AB//CD，ab//cd，a’b’//c’d’，a”b”//c”d”.AB/CD=ab/cd=a’b’/c’d’=a”b”/c”d”四、空间两直线的相对位置分为：⒈两直线平行投影特性：平abcdcabd例1：判断图中两条直线是否平行。

对于一般位置直线，只要有两个同面投影互相平行，空间两直线就平行。AB//CDabcdcabd例1：判断图中两条直线是否平行。bdcacbaddbac

对于投影面平行线，只有两个同名投影互相平行，不能判断空间直线平行。方法1：求出侧面投影AB与CD不平行。例2：判断图中两条直线是否平行。方法2：判断两线段是否同向且成比例。方法3：判断两直线是否在同一平面。判断四点同面即可。bdcacbaddbac对于HVABCDKabcdkabckdabcdbacdkk判别方法：

若空间两直线相交，则其同面投影必相交，且交点的投影必符合点的投影特性，反之亦然。（即两个垂直一个相等——交点的连线垂直于投影轴）。⒉两直线相交交点是两直线的共有点HVABCDKabcdkabckdabcdbadbaabcdc’dbaabcdc’●●cabbacdkkd例：过C点作水平线CD与AB相交。水平线的点Z坐标相等,即正面投影//OX轴.●●cabbacdkkd例：过C点作水平线CD与A例：作一正平线，使其与已知直线AB、CD和EF均相交。1232’3’1’正平线的点Y坐标相等,即水平投影//OX轴.例：作一正平线，使其与已知直线AB、CD和EF均相交。12e’eff’例.作一直线EF与直线AB、GH相交，并与直线MN平行。从特殊线AB积聚点得e，作EF//MN.e’eff’例.作一直线EF与直线AB、GH相交，并与直线dbaabcdc’1(2)3(4)投影特性：★同面投影可能相交，但“交点”不符合点的投影特性。★所谓“交点”是两直线上的一对重影点的投影。●●Ⅰ、Ⅱ是Ｖ面的重影点，Ⅲ、Ⅳ是H面的重影点。3

4●●⒊两直线交叉（既不平行又不相交）12●●dbaabcdc’1(2)3(4)投影特性：★例:判断两直线的相对位置baacddcbX11d1c1利用定比性判断CD上的点1的水平投影是否在ab上。点1不在水平投影的交点处，点1不是交点，所以两直线交叉。如果AB、CD相交，则CD上的1点应是两直线的共有点，即点1的水平投影应在AB的水平投影ab上。例:判断两直线的相对位置baacddcbX11平行交叉交叉相交Ｃk′Kk交叉相交作Ｃd=c′d′取dK=d′k′作Kk∥Cc本节到此平行交叉交叉相交Ｃk′Kk交叉相交作Ｃd=c′d′本节到此4、两直线垂直相交（或垂直交叉）1)两直线都//投影面投影反映直角。3)其中一直线//投影面的情况呢？cacbab.bacabcacbabc.？2)两直线都//投影面投影不反映直角。4、两直线垂直相交（或垂直交叉）1)两直线都//投影面4、两直线垂直相交（或垂直交叉）直角投影定理：若直角有一边平行于投影面，则它在该投影面上的投影仍为直角。已知：BC//H面，则BC⊥Bb，又BC⊥AB则BC⊥平面ABba两直线在H面上的投影相互垂直因此bc⊥ab即∠abc为直角又BC∥bc故bc⊥平面ABbaacbabc.证明：ABCabcb′a′c′HV垂直交叉呢？4、两直线垂直相交（或垂直交叉）直角投影定理：若直角有一边平dabcabc●●d例1：过C点作直线与AB垂直相交（即C点到AB的垂线---距离投影）。AB为正平线,正面投影反映直角。.dabcabc●●d例1：过C点作直线与AB垂直相精品课件！精品课件！精品课件！精品课件！(e′)f′ef真实距离分析：因AB⊥V，EF⊥AB，故EF//V面，为正平线，e’在a’（b’）的投影上;又EF⊥CD，要在投影图上画出来，EF只能为正平线或水平线，由以上得出，EF为正平线。所以，e’f’⊥c’d’;又EF为正平线,ef反映实长。即为AB、CD间的距离。例作交叉两直线AB、CD的公垂线EF，分别与AB、CD交于E、F，并标明AB、CD间的真实距离。(e′)f′ef真实距离分析：例作交叉两直线AB、CD的公直线的投影

两点确定一条直线，将两点的同面投影用直线连接，就得到直线的同面投影(粗实线2b,b细线宽)。

直线对一个投影面的投影特性一、直线的投影特性AB●●●●ab直线垂直于投影面投影重合为一点积聚性直线平行于投影面投影反映线段实长实形性ab=AB直线倾斜于投影面投影比空间线段短类似性ab=Abcosα●●AB●●abαAMB●a≡b≡m●●●aaabbb●●●●●●直线的投影两点确定一条直线，将两点的同面投影用直二、各种位置直线的投影特性（三大类七种）投影面平行线平行于某一投影面而与其余两投影面倾斜投影面垂直线水平线（平行于Ｈ面）正平线（平行于Ｖ面）侧平线（平行于Ｗ面）铅垂线（垂直于Ｈ面）正垂线（垂直于Ｖ面）侧垂线（垂直于Ｗ面）一般位置直线与三个投影面都倾斜的直线统称特殊位置直线（注意两者区别）垂直于某一投影面而与其余两投影面平行二、各种位置直线的投影特性（三大类七种）投影面平行线平行于

如图,直线AB与三个投影面都倾斜。V面投影a’b’,H面投影ab,W面投影a”b”。

设直线段AB对H、V、W三个投影面的倾角分别为α、β、γ，则ab=ABcosα,a’b’=ABcosβ,a”b”=ABcosγ.三个投影都具有类似性.投影特征：三斜无实长投影特性：1.三个投影长度都缩短，且与投影轴倾斜；2.其投影与投影轴的夹角，不反映直线对投影面的倾角。VHW

αβγ1.一般位置直线baabba

ABaa’’b’’a’b’b如图,直线AB与三个投影面都倾斜。V面投影a’b’2.投影面平行线与H面的倾角:α与V面的倾角:β与W面的倾角:γH面具有实形性,V、W有类似性。1.H面ab=AB,反映倾角β.γ；2.a’b’//OX,a”b”//Oyw，长度缩短。b1)水平线(//H,直线上点的Z坐标都相等)实长βγbaaabbα=？2.投影面平行线与H面的倾角:αH面具有实形性,V、W有V面具有实形性,H、W有类似性.

1.V面a’b’=AB,反映倾角α.γ；2.ab//OX,a”b”//OZ，长度缩短。baabab2)正平线（//V,所有点的Y坐标相等）γ实长αV面具有实形性,H、W有类似性.baabab2)正平baabba①

在其平行的那个投影面上的投影反映实长，并反映直线与另两投影面倾角的大小。②另两个投影面上的投影平行于相应的投影轴。3)侧平线（//W,所有点X坐标相等）投影特性：实长αβ投影特征：一斜两平行W面具有实形性,H、V有类似性.

1.W面a”b”=AB,反映倾角α.β；2.a’b’//OZ,ab//OYH，长度缩短。baabba①在其平行的那个投影面上的投影反映实长1.ab积聚成一点；2.a’b’⊥OX,a”b”⊥OYw,都反映实长。3.投影面垂直线1)铅垂线（⊥H面,所有点的X.Y相等）●aba(b)ab问α、β、γ？1.ab积聚成一点；3.投影面垂直线1)铅垂线（⊥H面,所有1.a’b’积聚成一点;2.ab⊥OX,a”b”⊥OZ,都反映实长。2)正垂线（⊥V面,所有点的X.Z相等）●a(b)abba1.a’b’积聚成一点;2)正垂线（⊥V面,所有点的X.Z3)侧垂线（⊥W面,Y和Z相等）②另外两个投影，反映线段实长，且垂直于相应的投影轴。①在其垂直的投影面上，积聚为一点。投影特性:●ababa(b)投影特征：一点两垂直1.a”b”积聚成一点；2.ab⊥OYH,a’b’⊥OZ,都反映实长。3)侧垂线（⊥W面,Y和Z相等）②另外两个投影，反映线段实直线上的点具有两个特性：1.从属性若点在直线上，则点的各个投影必在直线的各同面投影上。利用这一特性可以在直线上找点，或判断已知点是否在直线上。ABbbaaXOccCc三、直线与点的相对位置2.定比性直线上的点,分线段之比在投影中不变。即AC:

CB=ac:

cb=ac:

cb=ac

:

cb直线上的点具有两个特性：ABbbaaXOccCc三、点C不在直线AB上例1：判断点C是否在线段AB上。abcabc①c②abcab●点C在直线AB上根据点的从属性，若点的投影有一个不在直线的同名投影上，则该点必不在此直线上。对于一般位置直线两个投影就可以判断了。●●●点C不在直线AB上例1：判断点C是否在线段AB上。abca例2：判断点K是否在线段AB上。ab●k因k不在a

b上，故点K不在AB上。方法二：应用定比性abkabk●●方法一：应用从属性●●例2：判断点K是否在线段AB上。ab●k因k不在a例3已知点C在线段AB上，求点C的正面投影。bXaabccaccbXOABbbaacCcHV应用定比性（相似△）求例3已知点C在线段AB上，求点C的正面投影。bXa四、空间两直线的相对位置分为：平行、相交、交叉⒈两直线平行投影特性：

平行性——空间两直线平行，则其各同面投影必相互平行，反之亦然。aVHcbcdABCDbda等比性——空间两线段平行，其长度之比等于同面投影长度之比。⒈两直线平行

即：AB//CD，ab//cd，a’b’//c’d’，a”b”//c”d”.AB/CD=ab/cd=a’b’/c’d’=a”b”/c”d”四、空间两直线的相对位置分为：⒈两直线平行投影特性：平abcdcabd例1：判断图中两条直线是否平行。

对于一般位置直线，只要有两个同面投影互相平行，空间两直线就平行。AB//CDabcdcabd例1：判断图中两条直线是否平行。bdcacbaddbac

对于投影面平行线，只有两个同名投影互相平行，不能判断空间直线平行。方法1：求出侧面投影AB与CD不平行。例2：判断图中两条直线是否平行。方法2：判断两线段是否同向且成比例。方法3：判断两直线是否在同一平面。判断四点同面即可。bdcacbaddbac对于HVABCDKabcdkabckdabcdbacdkk判别方法：

若空间两直线相交，则其同面投影必相交，且交点的投影必符合点的投影特性，反之亦然。（即两个垂直一个相等——交点的连线垂直于投影轴）。⒉两直线相交交点是两直线的共有点HVABCDKabcdkabckdabcdbadbaabcdc’dbaabcdc’●●cabbacdkkd例：过C点作水平线CD与AB相交。水平线的点Z坐标相等,即正面投影//OX轴.●●cabbacdkkd例：过C点作水平线CD与A例：作一正平线，使其与已知直线AB、CD和EF均相交。1232’3’1’正平线的点Y坐标相等,即水平投影//OX轴.例：作一正平线，使其与已知直线AB、CD和EF均相交。12e’eff’例.作一直线EF与直线AB、GH相交，并与直线MN平行。从特殊线AB积聚点得e，作EF//MN.e’eff’例.作一直线EF与直线AB、GH相交，并与直线dbaabcdc’1(2)3(4)投影特性：★同面投影可能相交，但“交点”不符合点的投影特性。★所谓“交点”是两直线上的一对重影点的投影。●●Ⅰ、Ⅱ是Ｖ面的重影点，Ⅲ、Ⅳ是H面的重影点。3

4●●⒊两直线交叉（既不平行又不相交）12●●dbaabcdc’1(2)3(4)投影特性：★例:判断两直线的相对位置baacddcbX11d1c1利用定比性判断CD上的点1的水平投影是否在ab上。