初中数学北师大八年级下册（2023年修订） 平行四边形教学设计

1、 多边形的内角和与外角和 教学设计土黄中学 李丛文【教学目标设计】知识与技能目标：掌握多边形内角和定理，进一步了解转化的数学思想过程与方法目标：经历质疑、猜想、归纳等活动，发展学生的合情推理能力，积累数学活动的经验，在探索中学会与人合作，学会交流自己的思想和方法情感与态度价值观目标：体验猜想得到证实的成功喜悦和成就感，在解题中感受生活中数学的存在，体验数学充满着探索和创造教学重点：多边形内角和定理的探索和应用教学难点：多边形内角和公式的推导；转化的数学思维方法的渗透【教学过程设计】第一环节创设现实情境，提出问题，引入新课1多媒体展示蜂窝，教师结合图片让学生发现生活中无处不在的多边形2在PPT上

2、展示房屋外形、生活用品，让学生发现人类的生活离不开多边形？第二环节概念形成1借助多媒体显示一多边形，学生类比三角形的有关知识对多边形定义、并表示出相应的元素2教师再给出严格规范的定义，特别借助学具说明“在平面内” 的必要性此外，说明正多边形的定义第三环节活动探究1、教师用两个三角形拼成长方形，示意学生可以将长方形分成两个三角形来求矩形的内角和为360。（以四人小组为单位展开探究活动）提出问题：三角形的内角和为180，那么多边形的内角和是多少度呢？从四边形开始研究活动一：利用四边形探索四边形内角和要求：先独立思考再小组合作交流完成）（师巡视，了解学生探索进程并适当点拨）（生思考后交流，把不同的方

3、案在纸上完成）（组间交流，教师课件展示几种方法）教师帮助学生反思：在刚才的探索活动中，大家有不同的方法求四边形的内角和，这些看似不同的方法有没有相似之处？进而引导学生得出：我们是把四边形的问题转化成三角形，再由三角形内角和为180，求出四边形内角和为360，从而使问题得到解决！进一步提出新的探索活动。活动二：探索五边形与六边形内角和（要求：独立思考，自主完成）注：在探究过程中，有学生是把五边形分割成四边形和一个三角形来解决问题的四边形内角和为360加上三角形内角和180，就求出五边形内角和为540，教师在肯定其做法的同时，要指出这种方法的局限性，即“必须在知道比其少一条边的多边形内角和的基础上

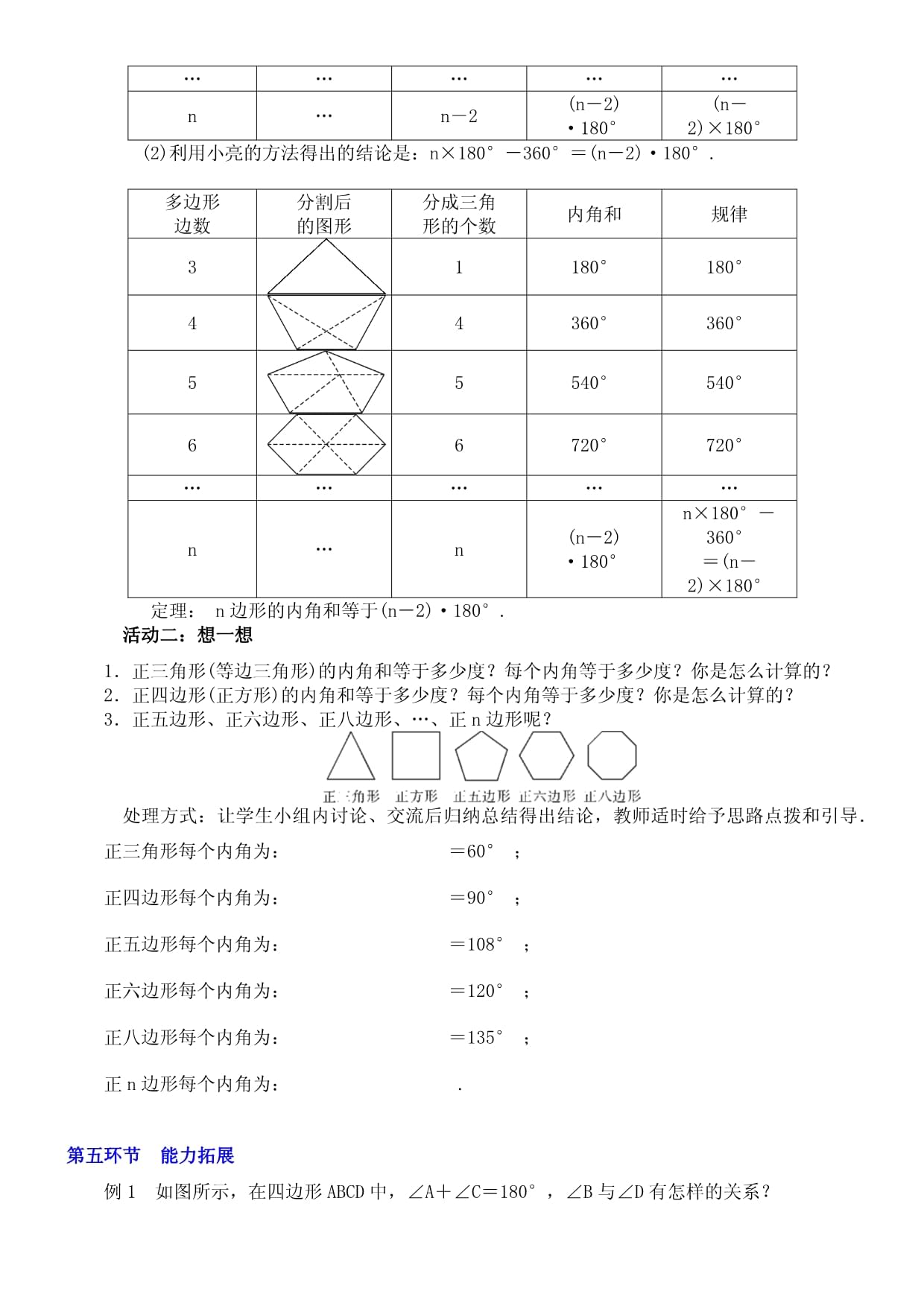
4、才能求出该多边形的内角和”第四环节思维升华活动一：想一想1按照活动一中的小明的方法，六边形能分成多少个三角形？n边形呢？你能确定n边形的内角和吗？(n是大于或等于3的自然数)小组讨论后完成表格多边形边数分割后的图形分成三角形的个数内角和规律3456n 2.按照活动一中的小亮的方法再试一试处理方式：学生动手画一画，分一分，教师对有困难的同学给予指导预设学生回答：(1)六边形可分成4个三角形，七边形可分为5个三角形，n边形可分为(n2)个三角形六边形内角和为720，七边形内角和为900，n边形的内角和为(n2)个三角形的内角和(n2)180(n 3)多边形边数分割后的图形分成三角形的个数内角和规律

5、31180180423603605354054064720720nn2(n2)180(n2)180(2)利用小亮的方法得出的结论是：n180360(n2)180.多边形边数分割后的图形分成三角形的个数内角和规律31180180443603605554054066720720nn(n2)180n180360(n2)180 定理： n边形的内角和等于(n2)180.活动二：想一想1正三角形(等边三角形)的内角和等于多少度？每个内角等于多少度？你是怎么计算的？2正四边形(正方形)的内角和等于多少度？每个内角等于多少度？你是怎么计算的？3正五边形、正六边形、正八边形、正n边形呢？ 处理方式：让学生小组

6、内讨论、交流后归纳总结得出结论，教师适时给予思路点拨和引导正三角形每个内角为：eq f(（32）180,3)60 ；正四边形每个内角为：eq f(（42）180,4)90 ；正五边形每个内角为：eq f(（52）180,5)108 ；正六边形每个内角为：eq f(（62）180,6)120 ；正八边形每个内角为：eq f(（82）180,8)135 ；正n边形每个内角为：eq f(（n2）180,n) .第五环节能力拓展例1如图所示，在四边形ABCD中，AC180，B与D有怎样的关系？ 处理方式：学生独立完成，教师适时指导点拨解：ABCD (42)180360，BD360(AC)3601801

7、80.B与D互补例2剪去一张长方形纸片的一个角后，纸片还剩几个角？这个多边形的内角和是多少度？与同伴交流预设学生可能回答：(1)如图所示，剪下一个角后，纸片剩下5个角，得到的五边形内角和为(52)180180. (2)如图所示，剪下一个角后，纸片剩下4个角，得到的四边形内角和为(42)180360.(3)如图所示，剪下一个角后，纸片剩下3个角，得到的三角形内角和为180.四、练习巩固1若一个多边形的每个内角都为120，则这个多边形的边数是()A9B8C7D62一个多边形的内角和为1 080，则这个多边形的边数为()A9 B8 C7 D63一个多边形截去一个角后，形成另一个多边形的内角和为720，那么原多边形的边数为()A5 B5或6C5或7 D5或6或74正十二边形每个内角的度数为_5有两个多边形，边数之比为34，内角和之比为12，求这两个多边形的边数应用发散：4如图所示的模板,按规定,AB,CD的延长线相交成80的角,因交点不在板上,不便测量，质检员测得BAE=122，DCF=155.如果你是质检员,如何知道模板是否合格?为什么? 5小明有一个设想：2023年奥运会在北京召开，要是能设计一个内角和是2023的多边形花坛该多有意义啊！小明的这个想法能实现吗？第六环节课时小结：教师和