2四边形综合应用(讲义及答案)

1、四边形综合应用（讲义）一、知识点睛1. 图形面积的处理方法公式法割补法转化法平行四边形中有关面积的常用处理手段三个“一半”ADAPDADS1S2S1O S2BCBCBCS1 S21 S ABCDS PBC1 S ABCDS1 S21 S ABCD222平行转化A PQDS1S2BCS PBCSQBCS1S22. 图形的平移在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移经过 平移， 对应点所连的线段 _；对应线段_ ， 对 应 角 _ ； 平 移 会 出 现_应用：如图，已知点 A，B， C，在平面内确定一点M，使以 A，B，C，M 为顶点的四边形是平行四边形M 2AM 1

2、BC二、精讲精练M 31. 如图，在 ABCD 中，过对角线 BD 上的一点 P，作 EFBC，HGAB若四边形 AEPH 和四边形 CFPG 的面积分别为 S1，S2，则 S1，S2 的大小关系为（）A S1S2B S1S2C S1S2D不能确定AHDEAHS1DEP2FBBGSCFCG第1题图第2题图2. 如图，五个平行四边形拼成一个含 30°内角的菱形 EFGH （不重叠无缝隙）若四个平行四边形的面积之和为 14cm2，四边形 ABCD的面积为 11cm2，则四个平行四边形的周长之和为（）A 48cmB36cmC24cmD18cm3. 如图，四边形 ABCD 和四边形 AEFC

3、 是两个矩形，点 B 在 EF 边上，若矩形1， S2，则 S1，S2 的大小关系为（）ABCD 和矩形 AEFC 的面积分别为 SA S1S2B S1S2C S1S2D 3S12S2ADDAEBCBCF第3题图第4题图4. 如图，在 ABCD 中，AC，BD 为对角线， BC=6，BC 边上的高为 4，则图中阴影部分的面积为（）A 3B6C12D245. 如图，在平面直角坐标系中， 四边形 ABCO 是正方形， 点 B 的坐标为 (4，4)，直线 y mx 2 恰好把正方形 ABCO 分成面积相等的两部分，则 m 的值为_yyABABCDMOCxExO第 5题图第6题图6. 如图，在平面直角

4、坐标系中，已知多边形 OABCDE 的顶点坐标分别是 O(0，0)，A(0，6)，B(4，6)，C(4，4)，D(6，4)，E(6，0)若直线 l 经过点 M(2，3)，且将多边形 OABCDE 分成面积相等的两部分，则下列各点在直线 l 上的是（）A(4，3)B(5，2)C(6，2)D(0， 10 )37. 如图，在 ABCD 中，点 E，F 在 AD 边上，且 AE=DF，连接 BE，CA，CE，CF，则图中与 CDF 面积相等的三角形共有 _个AEFDADGBCBEFC第7题图第8题图8. 如图，四边形 ABED 与四边形 AFCD 都是平行四边形， AF，DE 互相垂直，垂足为点 G，

5、点 B，E，F，C 在同一直线上 若 AG=3cm，DG=4cm，ABED的面积为36cm2，则四边形 ABCD 的周长为（）A 49cmB43cmC41cmD46cm9. 如图，将面积为 12cm2 的 ABC 沿 BC 方向平移至 DEF 的位置，若平移的距离是 BC 的 3 倍，则图中四边形 ACED 的面积为 _yCADBCEFO ABx第 9题图第 10题图10. 如图，在平面直角坐标系中，点 A，B 的坐标分别为 (1， 0)，(4，0)，点 C 在第一象限内， CAB=90°，且 BC=6将 ABC 沿 x 轴向右平移 ，当点 C 落在直 线 y 3x 2 3 上 时，

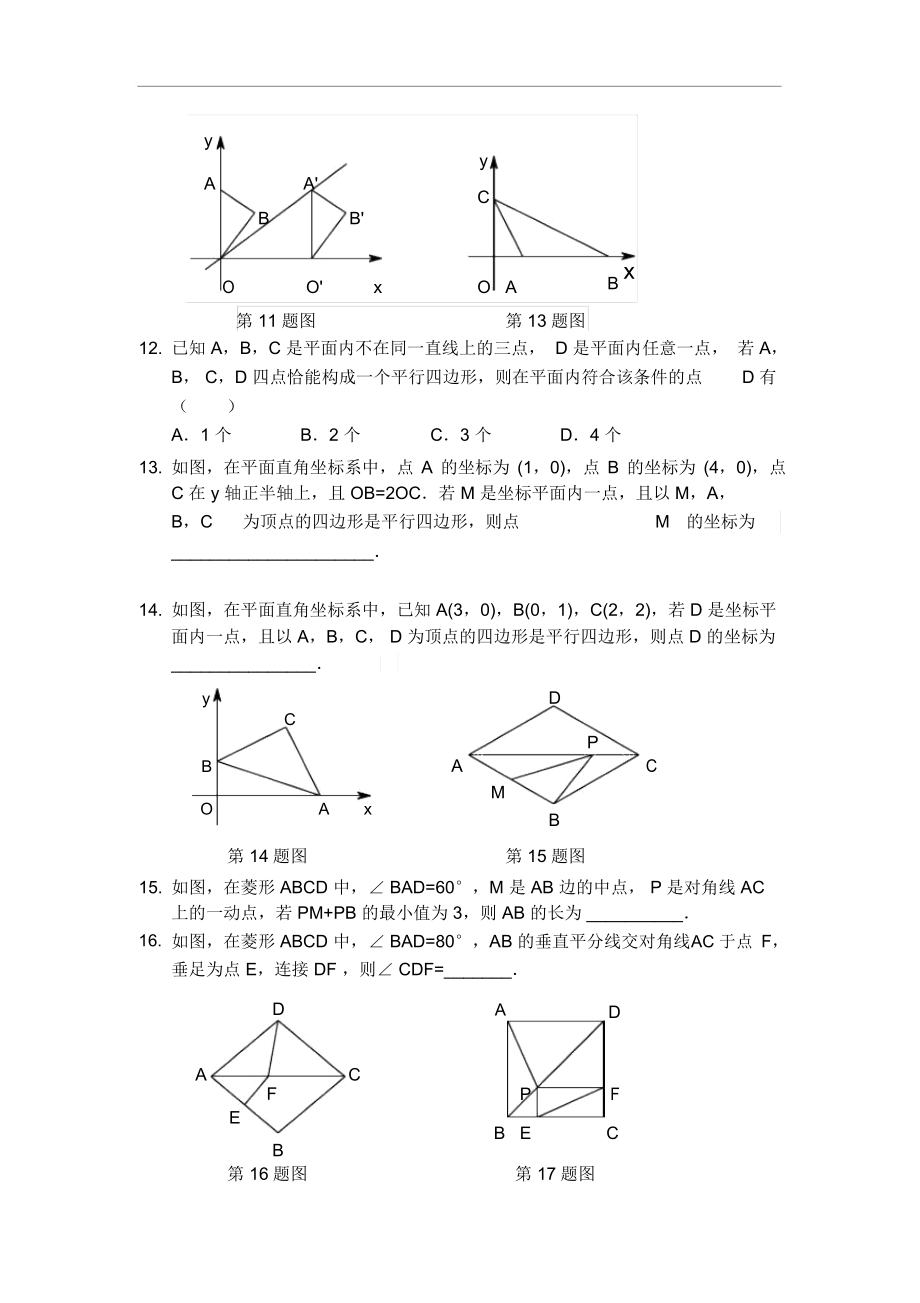
6、线段 BC 扫过 的面积为_11. 如图，在平面直角坐标系中，点 A 的坐标为 (0，3)， OAB 沿 x 轴向右平移后得到 OAB若点 A 的对应点 A为直线 y3 x 上一点，则点 B 与其对应4点 B间的距离为 _yyAA'CBB'OO'xO AB x第 11题图第 13题图12. 已知 A，B，C 是平面内不在同一直线上的三点， D 是平面内任意一点， 若 A，B， C，D 四点恰能构成一个平行四边形，则在平面内符合该条件的点D 有（）A1 个B2 个C3 个D4 个13. 如图，在平面直角坐标系中，点 A 的坐标为 (1，0)，点 B 的坐标为 (4，0)，

7、点 C 在 y 轴正半轴上，且 OB=2OC若 M 是坐标平面内一点，且以 M，A，B，C为顶点的四边形是平行四边形，则点M的坐标为_14. 如图，在平面直角坐标系中，已知 A(3，0)，B(0，1)，C(2，2)，若 D 是坐标平面内一点，且以 A，B，C， D 为顶点的四边形是平行四边形，则点 D 的坐标为 _yCDBAPCOAxMB第 14题图第 15题图15. 如图，在菱形 ABCD 中， BAD=60°，M 是 AB 边的中点， P 是对角线 AC 上的一动点，若 PM+PB 的最小值为 3，则 AB 的长为 _16.如图，在菱形 ABCD 中， BAD=80°，

8、AB 的垂直平分线交对角线AC 于点垂足为点 E，连接 DF ，则 CDF=_F，DADACPFFEB ECB第 16题图第 17题图17. 如图，已知正方形 ABCD 的边长为 4，P 是对角线 BD 上一点， PEBC 于点E， PF CD 于点 F，连接 AP， EF给出下列结论： PD= 2 EC；四边形 PECF 的周长为 8； APD 一定是等腰三角形； AP=EF其中正确结论的序号是 _四边形综合应用（习题）例 1：如图，在平面直角坐标系 xOy 中，多边形 OABCDE 的顶点坐标分别为 O(0，0)， A(0，2)，B(2，2) ，C(2，4)， D(4，4)， E(4， 0

9、)若过点 M(2， 1)的直线 MP （与 y 轴交于点 P）将多边形 OABCDE 分成面积相等的两部分， 则 P 点的坐标为_yyCDC2DAB2GA2 BFM2MOEx4E xO【思路分析】读题标注：梳理思路：要把多边形分成面积相等的两部分，考虑把它分为两个中心对称图形，使直线过该图形的中心即可延长 AB 交 DE 于点 F，把多边形分为一个正方形和一个矩形点 M 为矩形的中心； 连接 CF，BD 交于点 G，则点 G 为正方形的中心 过点 M， G 的直线与 y 轴的交点即为点 P由 B(2， 2)，D(4， 4)，根据中点坐标公式可得， G(3， 3)，结合 M(2，1)可知，直线

10、MG 的表达式为 y=2x- 3，则点 P 的坐标为 (0， - 3)例 2：如图，在平面直角坐标系 xOy 中，已知 A(0，1)，B(- 2，0)，C(- 1，2)，若D 是坐标平面内一点，且以A，B，C，D 为顶点的四边形是平行四边形，则点D的坐标为 _yD 3【思路分析】(- 1，2)y读题标注：CCD 2A (0，1)ABOx(- 2，0)BOxD 1梳理思路：D（，）？A，B，C，D平行四边形定点： A，B，C动点： D（1）当 AC，BC 作为一组邻边（ AB 为对角线）时，过点过点 A 作 BC 的平行线，相交于一点即为点D1 ；B 作AC 的平行线，(+1，- 1)CA(-

11、1，2)(0，1)BD(- 2，0)(- 1，- 1)（2）当 AC，AB 作为一组邻边（ BC 为对角线）时，过点 B 作 AC 的平行线，过点 C 作 AB 的平行线，相交于一点即为点 D2 ；(- 1， +1)AC(0，1)(- 1，2)BD(- 2，0)(- 3，1)（3）当 BC，AB 作为一组邻边（ AC 为对角线）时，过点 A 作 BC 的平行线，过点 C 作 AB 的平行线，相交于一点即为点 D3 (+2，+1)BA(- 2，0)(0，1)CD(- 1， 2)(1， 3)综上，满足条件的点D 的坐标为 (- 1， - 1)， (- 3， 1)或(1， 3)1. 如图，矩形 AB

12、CD 的对角线 AC，BD 相交于点 O，过点 O 的直线分别交 AD， BC 于点 E， F若 AB=2， BC=3，则图中阴影部分的面积为 _AEDAFDEOPBFCBC第 1题图第 2题图2. 如图，在菱形 ABCD 中，AC=2，BD=5，P 是对角线 AC 上任一点，过点 P 作PEAD，交 AB 于点 E，PFAB，交 AD 于点 F，则图中阴影部分的面积为_3. 如图，正方形 ABCD 的对角线相交于点 O，点 O 是正方形 OEFG 的一个顶点，若两个正方形的边长都为 1，则这两个正方形重叠部分的面积为_Gy5FA4D3CB2O1AE- 1 O1 2 3 4 5 xBC- 1第

13、 3题图第 4题图4. 如 图 ， 在 平 面 直 角 坐 标 系 x O y 中 ， 点 A ， C 的 坐 标 分 别 为(4，0)，(0， 2)，四边形 ABCO 是矩形（1）把矩形 ABCO 分成面积相等的两部分的直线有_条；这些直线都经过的点的坐标为 _（ 2）若直线ykx4 （ k0 ）把矩形ABCO 分成面积相等的两部分，则k=_，在图中画出这条直线5.如图，在平面直角坐标系xOy 中，多边形 OABCDE 的顶点坐标分别为O(0，0)，A(2，0)，B(2，2)，C(4，2)，D(4，4)，E(0，4)若过点 M(1，2)的直线 MP（与 y 轴交于点 P）将多边形yOABCD

14、E 分成面积相等的两部分，则直线 MP 的函数D解析式为 _E【思路分析】PMC读题标注：B梳理思路：要把多边形分成面积相等的两部分，考虑把它分为两OAx个中心对称图形，使直线过该图形的 _即可把 多 边 形 分 为 一 个 _ 和 一 个_，点 M 为_的中心，取 _的中心为点 G，则直线 MG 即为所求由 B(2， 2)，D(4，4)，根据 _可得， G(3，3)，结合 M(1，2)可知，直线 MP 的表达式为 _6. 如图，将面积为 5 的 ABC 沿 BC 方向平移至 DEF 的位置，若平移的距离是边 BC 长的两倍，则图中的四边形ACED 的面积为 _yADBy=x 1BCEOAxF

15、第6题图第7题图7. 如图，Rt AOB 的直角边 OA，OB 分别在 x 轴、y 轴上，点 A，B 的坐标分别为(3，0)， (0，4)，将 AOB 向右平移，当点B 落在直线 yx1上时，线段AB 扫过的面积为 _8.如图，在平面直角坐标系 xOy 中，已知 A(1，- 1)，B(2，0)，若 C 是坐标平面内一点，且以 A，B，C，O 为顶点的四边形是平行四边形，则点 C 的坐标为_y【思路分析】读题标注：梳理思路：C（，）？A， B， C，O平行四边形OBxA定点： _，_， _动点： _（1）当 _， _作为一组邻边（ _为对角线）时，过点 _作 _的平行线，过点 _作 _的平行线，

16、相交于一点即为点_；(，)(，)(，)(，)(，)（2）当 _， _作为一组邻边（ _为对角线）时，过点 _作 _的平行线，过点 _作 _的平行线，相交于一点即为点_；(，)(，)(，)(，)(，)（3）当 _， _作为一组邻边（ _为对角线）时，过点 _作 _的平行线，过点 _作 _的平行线，相交于一点即为点_( ，)( ， )( ， )( ， )( ， )综上，满足条件的C 点坐标为 _9. 如图，在平面直角坐标系 xOy 中，已知 A(- 2，5)， B(- 3，- 1)，C(1，- 1)，若 D 是坐标平面内一点，且以 A， B，C，D 为顶点的四边形是平行四边形，则点 D 的坐标为 _【思路分析】yA读题标注：梳理思路：D（，）？OxA，B，C，D平行四边形BC定点： _，_， _动点： _（1）当 _， _作为一组邻边（ _为对角线）时，过点 _作 _的平行线，过点 _作 _的平行线，相交于一点即为点_；(，)(，)(，)(，)(，)（2）当 _， _作为一组邻边（ _为对角线）时，过点 _作 _的平行线，过点 _作 _的平行线，相交于一点即为点_；(，)(，)(，)(，)(，)（3）当 _， _作为一组邻