高等数学11.3多元复合函数与 隐函数的微分法ppt课件

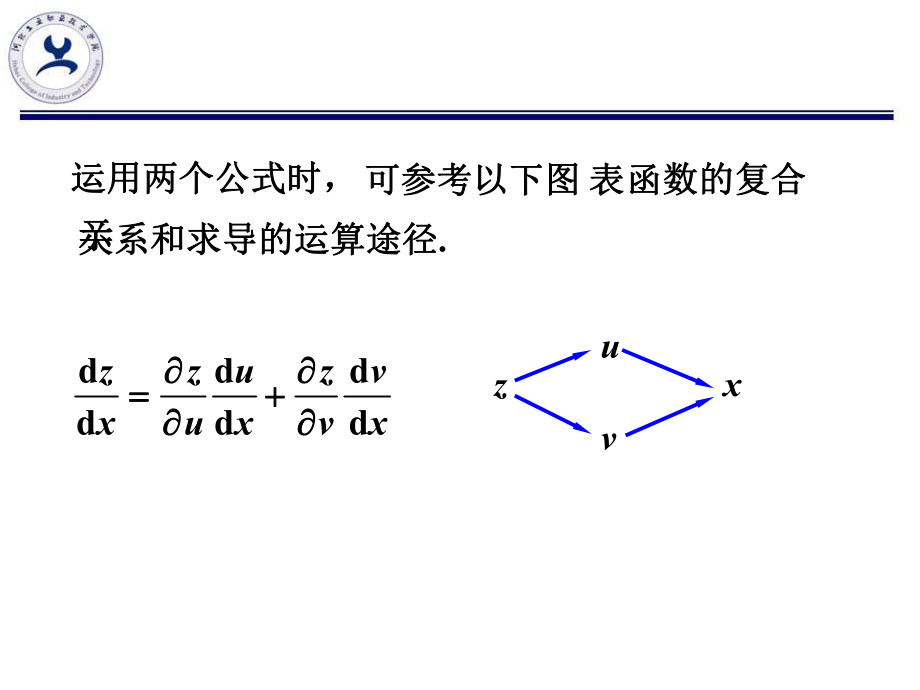
1、高高 等等 数数 学学主讲人主讲人 宋从芝宋从芝河北工业职业技术学院河北工业职业技术学院11.3 11.3 多元复合函数与隐函数的微分法多元复合函数与隐函数的微分法 设一元函数设一元函数 u = (x) 与与 v = (x) 在在 x 处均处均可导，可导，一、多元复合函数求导法那么一、多元复合函数求导法那么定理定理且为且为ddzx处有一阶延续偏导数处有一阶延续偏导数,vzuz 二元函数二元函数 z = f (u , v)在在 x 的对应点的对应点(u , v) 对对 x 的导数存在，的导数存在，(,)zfxx ( ( ) ) ( ( ) )那么复合函数那么复合函数zu ddux zv ddvx

2、 可参考以下图可参考以下图 表表示示 函数的复合函数的复合关系和求导的运算途径关系和求导的运算途径.运用两个公式时，运用两个公式时，zuvxddddddzzuzvxuxvx 例例 1设设,vuz ,2sin xu ,12 xv求求.ddxz解解 因因,1 vvuuz.lnuuvzv ,2cos2ddxxu .1dd2 xxxv那么那么 xzddxuvv2cos21 1ln2 xxuuv 1ln2cos22xuxuxvuv.1)2ln(sin2cot12)2(sin2212 xxxxxxx设函数设函数 z = f (u , v) 可微，可微， 这时，复合这时，复合函数函数 z = f u(x ,

3、 y), v (x , y) 对对 x 与与 y 的偏导数的偏导数都存在且都存在且,xvvzxuuzxz .yvvzyuuzyz 而而 和和),(yxu ),(yxv 的一阶偏导数都存在，的一阶偏导数都存在，zuvxy例例 2设设 z = eu cos v，,xyu ,2yxv . yzxz ，求求解解 由于由于,cosevuzu ;sinevvzu ,yxu ;2 xv,xyu .1 yv可得可得 xz2sinecose vyvuu)sin2cos(evvyu ,)2sin(2)2cos(eyxyxyxy yz)1(sinecose vxvuu)sincos(evvxu .)2sin()2c

4、os(eyxyxxxy 当当 z = f (u , v , w ), ),(yxu , ),(yxv 时时， ),(yx 其求导公式可参考关系图如下其求导公式可参考关系图如下 .zuvwxy xzxuuz xvvz ,xwwz yzyuuz yvvz .ywwz 又如又如 z = f (u , v ) ,),(tyxu ,),(tyxv 那那么么,xvvzxuuzxz ,yvvzyuuzyz .tvvztuuztz 例例 3，设设)sin,2,( xyyxxyfz 求求xz 与与.yz 解解,xyu 令令,2yxv ,sin xyw 于是于是).,(wvufz 由于由于,2xyxu , 1 x

5、v,cos xyxw ,1xyu , 2 yv,sin xyw 所以所以 xz 2xyfuxyffwvcos1 ,cos3212fxyffxy 式中的式中的 f i 表示表示 z 对第对第 i 个中间变量的偏导数个中间变量的偏导数 (i = 1 , 2 , 3)， 有了这种记法，有了这种记法， 就不一定要明显地写出中就不一定要明显地写出中间变量间变量 u， v， w .类似地，类似地，可求得可求得 yz.sin21321fxffx 例例 4 设设),(yxyxfxyz .,yzxz 求求例例 4 设设),(yxyxfxyz .,yzxz 求求解解在这个函数的表达式中，在这个函数的表达式中， 乘

6、法中有复合函乘法中有复合函数，数，所以先用乘法求导公式所以先用乘法求导公式. xz ),(yxyxfy 1121 ffxy ),(yxyxfy ,21ffxy yz .),(21ffxyyxyxfx ),(yxyxfx )1(121 ffxy二、隐函数的求导公式二、隐函数的求导公式1. 1. 一元隐函数的求导公式一元隐函数的求导公式设方程设方程 F (x , y) = 0 确定了函数确定了函数 y = y(x)， 两端两端对对 x 求导，求导，得得,0dd xyFFyx, 0 yF若若那那么么.ddyxFFxy 这就是一元这就是一元 隐函数的求导公式隐函数的求导公式.例例 5 5设设,222x

7、yx 求求.ddxy解解,2),( 22xyxyxF 令令那那么么,22 xFx,2yFy 由公式得由公式得 xydd.1222yxyx 2. 2. 二元隐函数的求导公式二元隐函数的求导公式 设方程设方程 F (x , y , z) = 0 确定了隐函数确定了隐函数 z = z (x , y),假设假设 Fx，Fy，Fz 延续延续，, 0 zF且且 两边分别对两边分别对 x ，y 求导，求导， 得得, 0 xzFFzx. 0 yzFFzy这就是二元隐函数的求导公式这就是二元隐函数的求导公式.zyzxFFyzFFxz ,0, zF因因为为所以所以例例 6, zxyz 设设求求.dz解解由于由于,lnzzFxx ,1 zyyzF,ln1yyxzFzxz 所以所以,lnln1yyzxzzxzzxx 令令.),(zxyzzyxF 故故xxzyyzzzxzxdlnlnd1 .lnd11yyzxyyzzxz ,ln11yyzxzyyzzxz 例例 7 设设,432222 zyx求求.,2yxzxz 解解 令令.432),(222 zyxzyxF,2xFx ,4yFy .6zFz 所以所以 xz zx62,3zx yz,3264zyzy 再求二阶导数，再求二阶导数，有有 xzyyxz2 z