编译原理及实现课后答案

5.1考虑以下的文法：

S-S;T|T

Tfa

(1)为这个文法构造LR(0)的项目集规范族。

(2)这个文法是不是LR(0)文法？如果是，则构造LR(0)分析表。

(3)对输入串“a;a”进行分析。

解：

(1)拓广文法G[S']：

0：S'-S

1：S-S;T

2：S-T

3：T-a

构造LR(0)项目集规范族

状态项目集转换函数

0S'・SG0[0,S]=l

S-・S;TG0[0,S]=l

S-・TG0[0,T]=2

T—♦aG0[0,a]=3

1S'—S・ACCEPT

S-S・；TGO[1,;]=4

2S->T•R2

3T—a・R3

4S-S;*TGO[4,T]=5

T—♦aG0[4,a]=3

5S—S;T・RI

(2)该文法不存在“归约一归约”和“归约一移进”冲突，因此是LR(0)文法。LR(0)分析

表如下：

ACTIONGOTO

状态

?a#ST

0S312

1S4ACCEPT

2R2R2R2

3R3R3R3

4S35

5RIRIRI

(3)对输入串“a;a”进行分析如下:

步骤状态栈符号栈输入符号栈ACTIONGOTO

00#a;a#S3

103#a;a#R32

302#T;a#R21

401#S;a#S4

5014#s；a#S3

60143#S;anR35

70145#S;TnRI1

801#SACCEPT

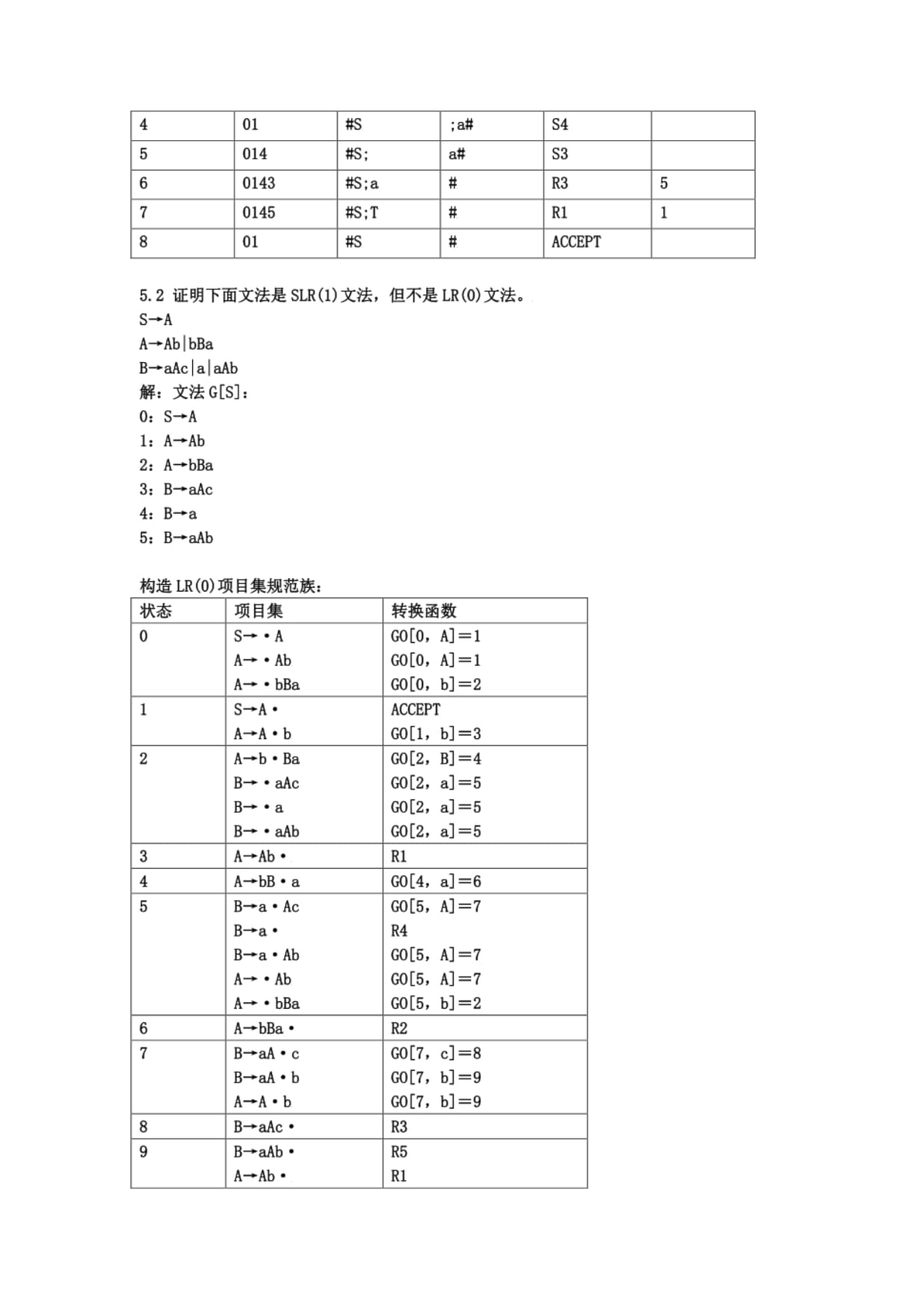
5.2证明下面文法是SLR(l)文法，但不是LR(O)文法。

S-*A

A—Ab|bBa

B-*aAc|a|aAb

解：文法G[S]：

0：S-A

1：AfAb

2：A-**bBa

3：B-aAc

4：Bfa

5：B—aAb

构造LR(0)项目集规范族:

状态项目集转换函数

0Sf・AG0[0,A]=l

A—•AbG0[0,A]=l

A—•bBaG0[0,b]=2

1SfA•ACCEPT

A-A•bGO[1,b]=3

2A—b•BaGO[2,B]=4

Bf•aAcGO[2,a]=5

B-**aGO[2,a]=5

Bf•aAbGO[2,a]=5

3AfAb•RI

4A--bB,aGO[4,a]=6

5B-a-AcGO[5,A]=7

B-a・R4

B—a•AbGO[5,A]=7

A->・AbGO[5,A]=7

A-**bBaGO[5,b]=2

6A—bBa•R2

7BfaA•cGO[7,c]=8

B—aA•bGO[7,b]=9

AfA•bGO[7,b]=9

8B—aAc•R3

9BfaAb•R5

A—Ab-RI

状态5存在“归约一移进”冲突，状态9存在“归约一归约”冲突，因此该文法不是LR(O)

文法。

状态5：

FOLLOW(B)={a},因此，FOLLOW(B)n{b}=6

状态9：

FOLLOW(B)={a},FOLLOW(A)={#,b,c),因此FOLLOW(B)DFOLLOW(A)=①

状态5和状态9的冲突均可用SLR(l)方法解决，构造SLR(l)分析表如下：

ACTIONGOTO

状态

abc#AB

0S21

1S3ACCEPT

2S54

3RIRIRI

4S6

5R4S27

6R2R2R2

7S9S8

8R3

9R5RIRIRI

该SLR(l)分析表无重定义，因此该文法是SLR(1)文法，不是LR(O)文法。

5.3证明下面文法是LR(1)文法，但不是SLR(l)文法。

S-*AaAb|BbBa

A—e

Bfe

解：拓广文法G[S']：

0：S'fs

1：S-AaAb

2：S-BbBa

3：Ai

4：B-e

构造LR(0)项目集规范族:

状态项目集转换函数

0S'—・SG0[0,S]=l

S-**AaAbG0[0,A]=2

S-・BbBaGO[0,B]=3

A-**R3

B-・R4

1S'--s・ACCEPT

2S-*A•aAbG0[2,a]=4

3S-*B•bBaG0[3,b]=5

4S-*Aa•AbG0[4,A]=6

A一,R3

5S-*Bb•BaG0[5,B]=7

Bf•R4

6S-*AaA•bG0[6,b]=8

7S-BbB-aG0[7,a]=9

8SfAaAb•RI

9S—BbBa•R2

状态0存在“归约一归约”冲突，且FOLLOW(A)={a,b},FOLLOW(B)={a,b},即FOLLOW(A)

AFOLLOW(B)={a,b}H①，所以该文法不是SLR(1)文法。

构造LR(1)项目集规范族:

状态项目集转换函数

0S'・S,#G0[0,S]=l

S—•AaAb,#G0[0,A]=2

S->•BbBa,#G0[0,B]=3

A—•,aR3

Bf・，bR4

1S'~S・，#ACCEPT

2SfA•aAb,#G0[2,a]=4

3S-*B•bBa,#G0[3,b]=5

4SfAa•Ab,#G0[4,A]=6

A一•,bR3

5S-*Bb•Ba,#G0[5,B]=7

B-*•,aR4

6S-AaA•b,#G0[6,b]=8

7S-*BbB•a,#G0[7,a]=9

8SfAaAb,,#RI

9S-BbBa・，#R2

LR⑴分析表:

ACTIONGOTO

状态

abSAB

0R3R4123

1ACCEPT

2S4

3S5

4R36

5R47

6S8

7S9

8RI

9R2

分析表无重定义，说明该文法是LR(1)文法，不是SLR(l)文法。

5.4考虑以下的文法：

E—EE+

E^EE*

E-*a

(1)为这个文法构造LR(1)项目集规范族。

(2)构造LR⑴分析表。

(3)为这个文法构造LALR(l)项目集规范族。

(4)构造LALR⑴分析表。

(5)对输入符号串“aa*a+”进行LR⑴和LALR(1)分析。

解：

(1)拓广文法G[S]：

0：SfE

1：EfEE+

2：EfEE*

3：Efa

构造LR⑴项目集规范族：

状态项目集转换函数

0Sf・E,#G0[0,E]=l

E->・EE+,a:#G0[0,E]=l

E-**EE*,a:#G0[0,E]=l

Ef•a,a:#GOEO,a]=2

1SfE・，#ACCEPT

E-*E•E+,a:#G0[l,E]=3

EfE•E*,a:#G0[LE]=3

E-*•EE+,*:+G0[l,E]=3

Ef•EE*,*:+G0[LE]=3

E—・a,*:+G0[La]=4

2Efa•,a:#R3

3EfEE•+,a:#G0[3,+]=5

E-EE•*,a:#G0[3,*]=6

EfE•E+,*:+G0[3,E]=7

E-E*E*,*:+G0[3,E]=7

Ef・EE+,*:+G0[3,E]=7

Ef・EE*,*:+G0[3,E]=7

E—・a,*:+G0[3,a]=4

4E-a*,*:+R3

5EfEE+・,a:#RI

6E-EE*•,a:#R2

7EfEE-+,*:+G0[7,+]=8

EfEE•*,*:+G0[7,*]=9

E—E・E+,*:+G0[7,E]=7

E->E*E*,*:+G0[7,E]=7

Ef•EE+,*:+G0[7,E]=7

Ef-EE*,*:+G0[7,E]=7

E-**a,*:+G0[7,a]=4

8EfEE+*,*:+RI

9E-EE**,*:+R2

(2)构造LR⑴分析表

ACTIONGOTO

状态

+*anE

0S21

1S4ACCEPT3

2R3R3

3S5S6S47

4R3R3

5RIRI

6R2R2

7S8S9S47

8RIRI

9R2R2

(3)构造LALR(l)项目集规范族:

状态项目集转换函数

0S->・E,#G0[0,E]=l

E-・EE+,a:#G0[0,E]=l

Ef・EE*,a:#G0[0,E]=l

E—•a,a:#G0[0,a]=2

1SfE•,#ACCEPT

EfE•E+,a:#GO[1,E]=3

E-*E,E*,a:#GO[1,E]=3

Ef・EE+,*:+G0[l,E]=3

E—・EE*,*:+GO[1,E]=3

E-•a.*:+GO[1,a]=2

2Efa•,a:#:*:+R3

3E~EE・+,a:#:*:+G0[3,+]=4

E—EE・*,a:#:*：+G0[3,*]=5

EfE・E+,*:+G0[3,E]=3

E—E*E*,*:+G0[3,E]=3

Ef・EE+,*:+G0[3,E]=3

E—・EE*,*:+G0[3,E]=3

E-•a,*:+G0[3,a]=2

4EfEE+・,a:#:*:+RI

5E—EE*・,a:#:*:+R2

(4)构造LALR⑴分析表。

状态ACTIONGOTO

+*a#E

0S21

1S2ACCEPT3

2R3R3R3R3

3S4S5S23

4R1R1RIRI

5R2R2R2R2

(5)对输入符号串“aa*a+”进行LR(D分析:

步骤状态栈符号栈输入串ACTIONGOTO

10#aa*a+#S2

202a*a+#R31

301#Ea*a+#S4

4014#Ea*a+#R33

5013#EE*a+#S6

60136#EE*a+#R21

701#Ea+#S4

8014#Ea+#R33

9013#EE+#S5

100135#EE+RI1

1101#E#ACCEPT

对输入符号串“aa*a+”进行LALR(l)分析:

步骤状态栈符号栈输入串ACTIONGOTO

10#aa*a+#S2

202#aa*a+#R31

301#Ea*a+#S2

4012#Ea*a+#R33

5013#EE*a+#S5

60135#EE*ai#R21

701#Ea+#S2

8012#Ea+#R33

9013#EE+#S4

100134#EE+RI1

1101#EACCEPT

5.5说明以下的文法是LR(1)文法，但不是LALR(l)文法。

S-*aAd|bBd|aBe|bAe

A-*c

B-*c

解：

拓广文法：

0：S'fS

1：SfaAd

2：S—bBd

3：S-aBe

4：S-*-bAe

5：A—c

6：Bfc

构造LR⑴项目集规范族

状态项目集转换函数

0S'・S,#G0[0,S]=l

S一,aAd,#G0[0,a]=2

Sf・bBd,#G0[0,b]=3

S—,aBe,#G0[0,a]=2

Sf•bAe,#G0[0,b]=3

1S'fS・,#ACCEPT

2Sfa•Ad,#GO⑵A]=4

S-*a-Be,UG0[2,B]=5

A—,c>dG0[2,c]=6

Bf•c,eGO⑵c]=6

3S~b・Bd,#G0[3,B]=7

Sfb•Ae,#G0[3,A]=8

Af•c,eG0[3,c]=9

B—,c,dG0[3,c]=9

4SfaA•d,#G0[4,d]=10

5SfaB,e,#GOS,e]=ll

6A—c•,dR5

Bfc•,eR6

7S-*bB・d,#G0[7,d]=12

8S—bA・e,#G0[8,e]=13

9A—c•,eR5

Bfc•,dR6

10SfaAd•f#RI

11S—aBe•,#R3

12S-bBd•,#R2

13S->bAe•,#R4

构造LR⑴分析表:

ACTIONGOTO

状态

abcde#SAB

0S2S31

1ACCEPT

2S645

3S987

4S10

5S11

6R5R6

7S12

8S13

9R6R5

10R1

11R3

12R2

13R4

同核项目集合并，构造LALR(l)项目集规范族:

状态项目集转换函数

0S'・S,#G0[0,S]=l

S->・aAd,#G0[0,a]=2

S-**bBd,#G0[0,b]=3

S—•aBe,#G0[0,a]=2

S-**bAe,#G0[0,b]=3

1S'fS・,#ACCEPT

2S-a・Ad,#GO[2,A]=4

S-*a•Be,#GO[2,B]=5

A一,c,dGO[2,c]=6

B-**c,eGO[2,c]=6

3Si・Bd,#GO[3,B]=7

S-*b•Ae,#GO[3,A]=8

Af•c,eGO[3,c]=6

B—•c,dG0[3,c]=6

4S-aA・d,#G0[4,d]=9

5S-*aB•e,#G0[5,e]=10

6A-*c•»d:eR5

B-*c•,d:eR6

7S-bB•d,#G0[7,d]=ll

8S->bA•e,#GO®e]=12

9S->aAd-,#RI

10S-*aBe•,#R3

11S-*bBd•,#R2

12S—bAe•,#R4

构造LALR(l)分析表:

ACTIONGOTO

状态

abcdeSAB

0S2S31

1ACCEPT

2S645

3S987

4S10

5S11

6R5/R6R5/R6

7S12

8S13

9R1

10R3

11R2

12R4

从LR(1)分析表可以看出，分析表无重定义，因此该文法是LR(1)文法。

从LALR(l)分析表可以看出，分析表ACTI0N［6,d］和ACTIONS,e］存在重定义，因此该文法

不是LALR(l)文法。

7