排队论在医院门诊中的应用

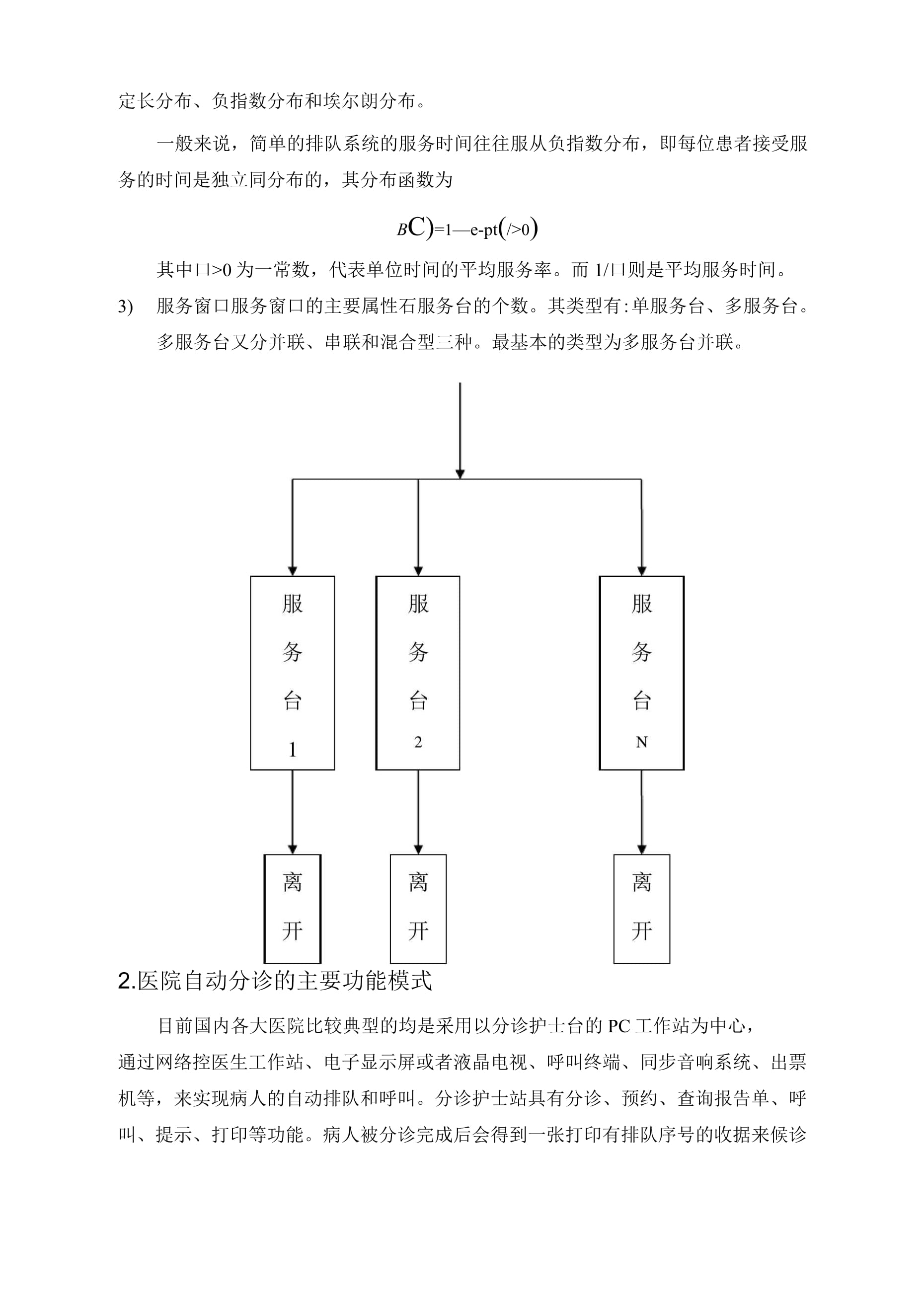
排队论在医院门诊中的应用摘要医院就医排队时一种经常遇见的非常熟悉的现象，它每天以这样或那样的形式出现在我们面前。例如，患者到医院就医、患者到药房配药、患者到输液室输液等，往往需要排队等待某种服务。经调查研究发现，不同于基于经验的管理方法，排队理论能较为科学，量化地分析医院的排队系统，并提出合理的整改意见。而国内正处于医院应用阶段的排队系统，大多都是凭经验建立的单一的门诊、体检、取药、检验、住院、结算等各环节的独立系统。由于各环节相对独立，病人依然很被动。这就需要提出一种能辅助并引导病人贯穿整个就诊流程的全流程排队解决方案，以缩短病人就诊时间，提高看病效率和病人满意度。如何在不增加医院运营成本的前提下，准确把握患者的主导需求，切实提高医院员工的服务效率，实现客户满意、医院获利的“双赢”目标是医院经营管理者积极追求的目标。本文分析门诊业务流程的运行规律,探寻流程需要再造的环节点,为门诊资源的优化配置和流程再造提供科学依据,同时证明采用排队论方法的合理性和可行性。方法采用排队论的理论与方法,通过随机测量某医院的门诊挂号、划价收费、内科和妇科服务节点的服务时间及患者到达时间,计算各节点服务强度、平均排队长、平均排队时间、平均逗留时间,服务台空闲概率和顾客到达后需要等待的概率等运行指标,推算合理的服务台数,并模拟计算患者等待成本和医院服务成本之和的最优值。关键词】：对长；等待时间；服务强度；排队模型；概率分布本篇论文围绕以下几点问题进行分析讨论：问题1：对排队系统做一个充分详细的说明与符号规定。问题2：现有的医院门诊模式统计与讨论研究。问题3,建立合理的评价指标体系,用以评价病床安排模型的优劣.问题4,举某一个实际生活中的具体例子，并且试就该医院当前的情况,在对大量历史数据进行详细统计分析的基础上，以排队论为理论依据，建立合理的窗口设置与安排模型,并对该利用问题3中的指标体系作出评价.问题5：对医院门诊排队问题给出相应的意见。结果案例医院当前门诊挂号、划价收费、内科的服务强度、人员配置、排队等候时间等基本合理。门诊妇科则须再增加一名医生,可提高该环节流程效率,减少患者等待时间及排队长等。当前该院设置医生不足,医院投人成本较小,而患者因等待而付出的成本偏高。结论应用排队论的理论与方法评价门诊服务流程效率合理可行,值得推广。排队论相关理论介绍与说明，排队论又称为随机服务系统的理论，是通过研究各种服务系统在排队等待现象中的概率特性，从而解决服务系统最优设计与最优控制的一门科学，是运筹学的一个重要分支。排队论的研究自开创之后不断完善，特别是在计算机技术的飞速发展，为他的应用开拓了宽阔的前景，现在已广泛应用于交通、医疗、商场购物，码头等行业排队过程，本文就医院门诊问题服务系统中最常见的排队模型的组成、运行指标以及排队论在测量门诊流效率中的作用做一研究。在我国，医院门诊部工作量大，一般常见病、多发病患者主要在门诊部就诊。患者的到达及接受就诊服务均受到许多种因素的影响，出现排队现象是不可避免的。一下将对医院门诊排队现象进行全面的分析，给出排队论系统的主要指标，为医院门诊部的质量评估、科学化的管理、缩短患者排队时间和就诊时间提供科学依据。1.1排队系统的组成与特征排队系统通常由输入过程、排队规则和服务机构三部分组成。输入过程:是指需要服务的顾客按何种规律到达排队系统的过程，也称顾客流。一般可从3个方面描述:顾客源是有限的还是无限的;顾客是单个到达还是成批到达;顾客相继到达的时间间隔是确定的还是随机的。在一定的时间间隔内，系统内到达K个顾客的概率有以下两种常见形式:①定长分布即顾客相继到达的时间间隔是确定的；②泊松分布(M)又称泊松过程，即顾客单个到来且相互独立，一定时间的到达数服从泊松分布，相继到达的时间间隔及期望值、方差均不受时间影响；具有平稳性无后效性、普通性等特征。常见的输入过程有定长输入、泊松(Poisson)输入、埃尔朗(A.K.Erlang)输入等，其中泊松输入在排队系统中的应用最为广泛。所谓泊松输入即满足一下4个条件的输入：平稳性：在某一时间区间内到达的患者数的概率只与这段时间的长度和患者数有关；无后效性：不相交的时间区间内到达的患者数是相互独立的；普通性：在同时间点上就诊或手术最多到达1个患者，不存在同时到达2个以上患者的情况；有限性：在有限的时间区间内只能到达有限个患者，不可能有无限个患者到达。4.1、患者的总体可以使无限的也可以是有限的；4.2、患者到来的方式可以是单个的，也可以是成批的；4.3、相继到达的间隔时间可以是确定的，也可是随即的；4.4、患者的到达可以是相互独立的，也可以是关联；4.5、到来的过程可以是平稳的，也可是非平稳的；1.1.2．排队规则:主要描述服务机构是否允许顾客排队，顾客对排队长度、时间的容忍程度以及在排队队列中等待服务的顺序。一般可以分为损失制、等待制和氓合制等3大类。①损失制：是指顾客到达排队系统时，因服务台都占用，顾客离开系统永不再来。考虑医疗需求弹性低，患者离开和不再回医院诊治的可能性较小，故医院门诊损失制情况较少。②等待制：这是指当顾客来到系统时，所有服务台都不是空闲状态，顾客加人排队行列等待服务。患者到达时，如果所有服务台都没有空闲，他们就排队等待。等待服务的次序又有各种不同的规则：2.1、先到先服务，如就诊、排队取药等；2.2、后到先服务，如医院处理急症病人；2.3、随即服务，服务台空闲时，随机挑选等待的患者进行服务；2.4、优先权服务，如照顾号。③混合制：是等待制与损失制相结合的一种服务规则，一般是指服务系统允许排队，但又不允许队列无限长。混合制既有等待又有损失的情况，患者等待是考虑排队的队长、等待时间的长短等因素而确定去留。队列的数目可是单列，也可是多列的；容量可能是有限的，也可能是无限的。1,1，3．服务机构:包括服务台的数量、服务台的排列方式及服务时间。服务台从数量上有单服务台和多服务台之分。排队方式从排列方式上有：单队——单服务台方式；单队——多服务台并联式；多队——多服务台并联式；单队——多服务台串联式；单队——多服务台并串联提合式；多队——多服务台并串联棍合式等。从服务方式上有单个服务和成批服务两种。按服务时间的不同规律可分为确定型或随机型。服务时间患者接受服务的时间规律往往也是通过概率分布描述的。常见的服务时间分布有定长分布、负指数分布和埃尔朗分布。一般来说，简单的排队系统的服务时间往往服从负指数分布，即每位患者接受服务的时间是独立同分布的，其分布函数为BC)=1—e-pt(/>0)其中口>0为一常数，代表单位时间的平均服务率。而1/口则是平均服务时间。服务窗口服务窗口的主要属性石服务台的个数。其类型有:单服务台、多服务台。多服务台又分并联、串联和混合型三种。最基本的类型为多服务台并联。2.医院自动分诊的主要功能模式目前国内各大医院比较典型的均是采用以分诊护士台的PC工作站为中心，通过网络控医生工作站、电子显示屏或者液晶电视、呼叫终端、同步音响系统、出票机等，来实现病人的自动排队和呼叫。分诊护士站具有分诊、预约、查询报告单、呼叫、提示、打印等功能。病人被分诊完成后会得到一张打印有排队序号的收据来候诊间医生的自动呼叫。3．3种分诊模式的比较根据医院管理模式不同，病人分诊模式可以分为挂号站分诊和护士站分诊，如果预检分诊无法无法准确到专科，而专科医生兼治其他专科的功能，则需要按护士站分诊模式，否则苦厄按挂号分诊模式操作。护士站分诊模式：该模式要求病人挂号后到候诊区护士站进行排队刷卡，由护士询问后病情和分配医生诊间，并打印号票，注明病人姓名、诊间号，医生姓名、排队序号等信息。病人通过大屏幕观察目前的队列情况，估计自己的就诊时间。此种模式的好处是分诊比较准确，护士可以视病人的病情和医生的资历经验给予准确分诊；此种模式的弊端是：如果病人错过了排队就诊时间的话，病人需要多排一次队伍，特别是病人多而护士站后台操作不熟练或者是计算机系统出现一些问题时，会出现护士站前排队长的状况；打引号票比较浪费时间和资源，污染诊区，同时多了一个故障点；护士工作量明显增大，压力倍增，同时对诊间的管理度相对下降。为此，我们这里将这种诊断模式改成了挂号站分诊的模式。护士站分诊模式一般比较适合B超室及放射科等特检科室的等候排队情况，病人缴纳费用后必须先到分诊台确定检查类型（如B超有心脏、腹部、阴道、儿童）及检查时间，并打印一张预约排队号票，病人凭票等候；预约病人到大医院后要先刷卡报到，以证明该病人已到达该医院，可以进行排队就诊。为此医院需增设病人自助刷卡排队机一台，用以病人刷卡和告知医院排队系统是否呼叫该病人或查询目前的排队等候人数，为刷卡的预约病人则被系统自动认为放弃治疗或者是爽约病人，暂时被搁置一边，知道刷卡为止。挂号站分诊模式：该模式要求在挂号室选择医生或者专科医生，在挂号单据上打印诊间序号、病人和医生相关信息等，病人进入诊区后无需在次分诊，只需要观察大屏幕的提示信息即可，这种方法既方便了病人也让分诊护士的工作量得以大量减少，具有较多的有点。但是这种模式存在的最大问题是如何让保证不懂医学知识的收费人员能为病人准确分诊。在我国的一些医院当中，病人挂号前需要进行准确的预检分诊到具体的专科，因此此类问题完全可以得到很好的解决，或者根本就不存在这样的问题。但是当该医院目前的预检只能是进行初略的分诊，还不能明确到专科，同时分诊力量也不够。因此，经过多次讨论确定了先修改挂号预检单的方案，即在挂号预检单中增加基本病情症状的选着框，由病人自行选择症状，挂号系统根据不同症状的组合可以择优选择专科，同时加强财务科人员的分诊知识的培训，经过一周的系统磨合，基本可以解决挂号同时分诊所存在的问题。但是在医院的儿科当中，存在专科医生兼看其他专科病人的情况，如当天坐诊呼吸专业的专家在本专业病人较少或者其他相关专业的病人过多时，必须能自动接诊其他专业的病人，为此在这里设计了智能分配功能，保证了所有病人能尽快获得最好的诊疗，而所有医生又能保证比较平衡的工作量，我们为当天坐诊的医生设置了一下参数：①主专业专科名称：医生当天的主要专业，只能设置一个主要专业；②副专业专科名称：医生当天可以接诊其他专业，可以设置多个副专业；③转出人数上限Y：即接诊次专业病人的临界点，当前医生的挂号总人数达到该数后可以转出给其他副专业的医生；④转入人数上限X：即接诊次数专业病人的上限数，当前医生的总挂号人数达到该数后不能继续接诊副专业病人⑤上午限号人数M:上午最多可以接诊的病人数；⑥下午限号人数M:下午12最多可以接诊的病人数。挂号分诊的算法如下：①当日存在相同专业的多个医生，并且候诊人数在Y以内时，选择该专业的时候人数最少得医生，若候诊人数已多于Y，则执行转出②；②存在次专业相同的多个医生，且该医生当前的候诊人数小于X,则选择次专业相同的候诊人数最少的医生分配给病人，否则执行③；③不存在次诊医生，继续分配给同专业的医生，选择候诊人数最少的医生，直至总就诊人数达到限号数量M为止。急诊分诊模式：医院儿童急诊主要是内科病人，患者较多，病人状况基本不一样，有一部分是真正需要急诊的，有一部分是普通平诊病人及中等偏重的病人，对于不同病人就诊速度应该有所区别，而各诊间医生此时的专业类型基本一致，大家都不希望只看急、重病人。因此分诊系统应能平均分配病人。为此我们设计了一下分诊方案：①挂号处尽负责挂号收费，不负责分诊；②分诊护士将病人分成急诊A、亚急诊B平诊C三种类型，病人到诊区后必须到护士站进行刷可并分类编号，如A010,代表急诊的第十号人。病人分诊后通过电子显示屏确定诊间；③分诊系统将A、B、C三类病人按5：3：1的比例（可调整）分配到各诊间医生，即所有医生看完5个急诊病人后再看3个亚急诊病人，最后看一个普通病人，如此，可以保证较重的病人得到最快就诊。4．以排队论观点分析医院门诊流程环节的特点医院门诊业务流程由许多单环节点首尾相接而成，通常包括：挂号、就诊、检查治疗、划价缴费、取药等。考虑患者在门诊服务过程中的实际特点，可以将流程看作是以串联为主，多服务台、存在循环的排队网络。以下是医院排队候诊流程图：门诊病人就诊流程图初诊未办诊疗卡I复诊以办诊疗卡详细填报诊疗卡录入表各楼层分诊台］丿收费窗口挂号、在卡中预存诊疗费用楼候诊区进入诊室刷卡就诊三楼候诊区看检查结果4住院一楼大厅住院处相关治疗收费窗口就诊结束，打印发票，办理退费楼候诊区进入诊室刷卡就诊三楼候诊区看检查结果4住院一楼大厅住院处相关治疗收费窗口就诊结束，打印发票，办理退费5、排队论几个常用的概率分布和最简单流5.1、负指数分布(记为M)一个随机变量g，他的分布密度函数为：TOC\o"1-5"\h\z人-At,t>0d>0)fc)=<其中A为常数；0,t<0称g服从参数为1的指数分布，又称g服从参数为1的负指数分布，分布AA函数为：1—e-At,t>0fc)=<0,t<0g的数学期望为E(g)=1，方差D(g)=亠。当t>0时，有AA2P(g>t)二1—F(t)=e-At负指数分布有重要用应用，常用它作为各种“寿命”分布的近似。例如无线电元器件的寿命、动物的寿命、电话问题中的通话时间等。排队论中的服务时间和顾客到达间隔时间都常常假定服从负指数分布。负指数分布g有一个重要的性质，即无记忆性或称无后效性。若把解释为电子元件的寿命，无记忆性就是不论现在的年龄多大，剩余寿命的条件分布与原分布相同，不受已有年龄的影响，用概率公式表示为P(g>t+xIg>t)=P(g>x)反过来，连续型随机变量的分布函数中，只有负指数分布具有无记忆性。5.2、最简单流通常把随即时刻出现的时间组成的序列称为随机事件流，列如用nQ表示(0,t］时刻内要求服务的顾客人数就是一个随机事件流现在我们提出在排队系统中常用的一种流——最简单流。如果一事件流{nC),t>0},满足下列三个条件，就称为最简单流。5.2.1、平稳性以任何时刻t为起点，C,t+1］时间内出现的事件数只与时间t长度有关，000而与起点t无关，因此用nQ表示C,t+1］出现的事件数，pC）表示nC）=k的000k概率，则PC）=P（NC）=k），k=0，1，2，...k£pC）=1kk=05.2.2、无后效性在C,t+1］时间内出现k个事件与t以前出现的事件数无关0005.2.3、普通性在充分小的时间At区间内，发生两个或两个以上事件的概率是比At高阶的无穷小量，即P（At）=£P（At）=o（At）k在上述三个条件下，可以推出P（t）=^^eJ，k=0，1，2,...kk!最简单流和与负指数分布有密切的关系。如果随即事件到达的间隔时间相互独立并且服从同一负指数分布，则这样的随机事件流都是最简单流。最简单流在显示世界中常遇到，如市内交通事故、稳定情形下电话呼唤次数、到车站等车的乘客数、上下班高峰过后通过路口的自行车流、人流、汽车流等都是或近似最简单流。一般来说，大量的稀有事件流，如果每一事件流在总事件流中起的作用很小，而且相互独立，则总的合成流可以认为是最简单流。5.3、生灭过程排队论中常用到的一类随机过程——生灭过程定义：设有某个系统，具有状态集S=｛0，1,2,3,...｝，若系统的状态随时间t的变化过程（VC）t>o｝满足以下条件，则称为一个生灭过程设在时刻t系统处于状态n的条件下，在经过长为At（微小增量）的时间（1）转移到n+1（0<n<+8）的概率为九At+o（At）；n转移到n-1(1<n<)的概率为卩At+o(At)；n转移到S--1,n,n+1｝的概率为o(At),其中九>0,卩>0为与t无关的固定常数。nn若S仅包含有限个元素，S=｛O,1,2，3,...，k｝，也满足以上条件，则称为有限状态生灭过程现在来讨论系统在时刻t处于状态n的概率分布，就是求PC)=P(NC)=n)，n=1，2，3，…t>0n设系统在时刻t+At处于状态n，这一事件可分为如下四个互不相容的事件之和。在时间t处于状态n，而在时刻t+At仍处于状态n，其概率为pC)G-九At-pAt)+o(At)；TOC\o"1-5"\h\znnn在时间t处于状态nT，而在时刻t+At仍处于状态n，其概率为PC\At+o(At)n-1n-1在时间t处于状态n+1,而在时刻t+At仍处于状态n，其概率为PChAt+o(At)n+1n+1在时间t处于别的状态(既不是n-1，n，n+1)，而在时刻t+At处于状态n。其概率为o(At)。由全概率公式，有P(t+At)=PC)G-九At-pAt)+P(thAt+P(kAt+o(At)；nnnnn+1n+1n-1n-1类似的，对n=0有P(At)=PC)(-九At)+PC)pAt+o(At)00011将上面诸式，右边不含At的想移到左边，用At除两边，然后令AtT0假设极限存在，就得到差微分方程：p0=九pC)-d+p)pC)+ppC)nn-1n-1nnnn+1n+1①p'C)=-九pC)+ppC)00011解这组方程组，即可得到时刻t系统的状态概率分布｛PC)nGS｝即生灭过程n的瞬时解。一般来说，解方程组①比较困难假设t*时，pC）的极限存在。n同时可以证明limP同时可以证明limP(/)tsnn=0，1，2，…limP'(t)=0,n=0,1,2,...tsn这样方程组①两边对t取极限，就得到线性方程组0=九pC）-（九+卩）p+卩pn-1n-1nnnn+1n+1,n=0,1,2,.②0=—九P+卩P0011移项后，②变成枕P-卩P=九P-卩Pnnn+1n+1n-1n-1nnv，n—0，1，2，・・・九P-卩P=00011所以九P-uP=九P-uP=九jPn一2nuP=.....-2n-1n-1.=九P-uP=00011nnn+1n+1n-1n-1nn则有九九九九九九P=P=n———n-1P==n—n-1...—0-Pn+1unuun-1uuu0n+1n+1nn+1n1假设0九九九<n—•―n■!•・・・・..•—<+8n=0n+1n1由于FP=1，就能解出nn=01—1—n-•—n-1•九•—0TOC\o"1-5"\h\zn=0n+1n，n=1,2,3,.九九九P=——n-1n2••―Pn□卩卩0nn-11这就是生灭过程在tT8时的状态概率，在大多数实际问题中，当t很大时，系统会很快趋近与统计平横。排队系统

6.1、M/M/1/g系统设顾客流是参数为九的最简单流，九是单位时间内平均到达的顾客人数，即顾客到达的时间间隔相互独立并且服从期望为1的负指数分布。只有一个服务九台，服务一个顾客的服务时间V服从参数为卩的负指数分布。平均服务时间为E(v)=丄，在服务台忙时，单位时间平均服务完的顾客数位卩。称p=-为服务强度。用NQ表示在时刻t顾客在系统中的数量(包括等待服务的和正在接受服务的顾客)。我们先来证明系统kC)t>o｝组成生灭过程。由于顾客的到达是最简单的流，参数为九，固有(t(t)=kk!，k=o,1,2,3，…..则在厂为At的时间内有一个顾客到达的概率为p(At)=九Ate-^At=九At(1—九At+—At2+...)=九At+o(At)12!没有顾客到达的概率为p(At)=e-^At=1-XAt+o(At)oSp(At)=Sp(At)=kk=2艺p(At)-p(At)-p(At)ko1k=0=e恥兰兽-po(At)-pi(At)k=0=e-九Ate九At-XAt-(1-XAt)+o(At)=o(At)在服务台忙时(总认为只要系统内有顾客，服务员就得进行服务)，顾客接受服务完毕离开系统的间隔时间为独立的、参数为卩的负指数分布。所以在系统忙时，输出过程为一最简单流，参数为卩。于是当系统忙时，在At时间区间内1个顾客被服务完的概率为^At+o(At)，没有顾客被服务玩的概率为1-^At+o(At)，两个或两个以上顾客被服务完的概率为o(At)，且卩与系统的顾客数无关，与微小时间区间的起点无关。对任意给定的t(>0),微小增量At，假设p(At)=p{N(t+At)=jIN(t)=i},i>0ij先考虑j=i+1的情况，当i>1时，p(At)二p{At时间内恰好到达1个顾客而没有顾客被服务完或恰好有ki,i+1个顾客到达并且k-1个顾客被服务完，k>2}=p{At时间内恰好到达1个顾客而没有顾客被服务完}+p{At时间内到达k个顾客而服务完k-1个顾客，k>2}=九At[1—uAt+o(At)]+o(At)=九At+o(At)当i=0时，P01(At)二p{N(t+At)二1IN(t)二0}=p{At时间内到达一个顾客}=XAt+o(At)p(At)=p{N(t+At)=i—11N(t)=i}i,i—1=p{At内无顾客到达且恰好服务完1个顾客或者到达k个顾客而服务完k+1个顾客，k>1}=p{At内无顾客到达并且恰好服务完1个顾客}+p{At内有k个顾客到达而且恰好服务完k+1个顾客，k>1}=(1—XAt+o(At))(uAt+o(At))+o(At)=uAt+o(At)P(At)二P{N(t+At)二jIN(t)二i}i,j=P{At内到达k个顾客而服务i+k-j个顾客，k>2}nn=0nn=0j>i+1=o(At)j>i+1P(At)二P{N(t+At)二jIN(t)二i}i,j=P{At内服务完k个顾客而到达j-i+k个顾客，k>2}TOC\o"1-5"\h\z=o(At)，j<i-1由以上结果，可知｛N(t);t>0｝是-一生灭过程，并且九=X,nn>0u=u,nn>1由生灭过程求平稳公式，得TOC\o"1-5"\h\z九.九九九P=—n-1n_20P=(—)nP=pnPnu.uu0u00nn-11由假设p=±<1，则n=0从而平稳分布为nn>nn>0p=1-p是排队系统中没有顾客的概率，也就是服务台空闲的概率，而p恰0好是服务台忙的概率。利用平稳分布可以求统计平衡条件下的平均队长L、平均等待队长L、顾q客平均等待时间W、平均逗留时间W等。q用N表示在统计平稳条件下系统的顾客数，平均队长L是N的数学期望L=E(N)=£nP=£n(1-p)pnnn=0n=0=(1—p)p£npn-1=(1一p)p£Cn)n=0=(L-=(L-p)p£Pnn=0=(L-p)p(丄］J-P丿用N表示在统计平横排队时，排队等待的顾客数，它的数学期望L=E（V）qqq就是在等待服务的平均顾客人数。L=E(V)=£(n-1)Pqn=1=£nPnn=£nPnn=1上Pnn=1=£nP-(1-P)n0n=0=L-G-P)=0E-Pp21-p现在来求平均等待时间W，当一个顾客进入系统时，系统中已有n个顾客q的概率为P，每个顾客的平均服务时间为丄，所以他平均等待时间为n丄，因n卩卩此W=£n丄P=丄艺nP

q口n口nn=0n=01()p九=门E(N丿=乔p)=HE再来求顾客的平均逗留时间（平均等待时间加上平均服务时间）W，1卩1卩一九平均队长L、平均等待队长L、平均逗留时间W、顾客平均等待时间W是qq排队系统的重要特征，这些反映了排队的服务质量，是顾客及排队系统设计者关系的几个指标，由上面四个公式，可以得到四个指标之间的关系L二L-（1-P）q0九W二L九W二Lqq

这三组关系试，可以这样直观解释：当系统内有顾客时，平均等待队长L应

q

该是平均队长L减1,当系统内没有顾客时，平均等待队长L与平均队长L相q等，所以L二L-K1-P）1+PL—6-P）q000单位时间内平均进入系统的顾客数为九个，每个顾客在系统内平均逗留W单位时间。因此系统内平均有九W个顾客，同样理由，系统内平均有九W个顾客在q等待服务。6.1、M/M/m/3系统现在来讨论多个服务台情况。假设系统有C个服务台，顾客到达时，若有空闲的服务台便立刻接受服务。若没有空闲的服务台，则排队等待，等到有空闲服务台时接受服务。与以前一样，假设顾客以最简单流到达，参数为九，服务台相互独立，服务时间都服从参数为口的负指数分布。当系统中顾客人数n<c时，这些顾客都正在接受服务，服务时间服从参数为口的负指数分布。可以证明顾客的输出是参数为ny的最简单流。如果n>c，那么只有c个顾客正在接受服务。其余在排队，顾客的输出服从参数为仲的最简单流。用N（t）表示t时刻排队系统内顾客人数。与M/M/1/的推导法类似，可以证明C）t>o｝也是一个生灭过程。nn=1nn=1由③得到九九——n-1pn—n-2•pn-1令P=-p九=九,nVn=0,l,2,3,|LX=Vnmp,九1Pp01m,m+1,m+2,...nP,0Cn-cc!(卩丿P,0n=0,1,2,,c-1n=c,c+1,=九mp£Pnn=0P+£Pnnn=0n=m厉1乙一P、n!n=011Pnm!cn-m丿n=m先计算平均等待队长Lq,nn!n=0m-11£Pnn!n=0£+PmPm!mn-mm1+Pmm!1-P丿m£-1Pnmpmn!m!(m-P)n=0-1只有系统中的顾客数n>m时，才有n-m个顾客PPmnm!0n=m在排队等待服务，所以L=£(n-m)p=-PmP艺(n-m\—\"

pnm!0(mp丿n=mPm的=PP£npn-1

m!m0mkkpm=Ppm!0mdP1-Pm-Popmpmp(1-p)2m!0mpPP(1-p)2mm平均忙的服务台数为n=0£m-1Pnn・Pn!0Emm•pnmPm!0n=mn=0n=1Pn-1(n-1)mm•PmP+mm-0m!Em・mm•pnmP

m!0n=m+1p送与P+n=0pm-1p(m-1)0mm-1•pn-1+p•乙-Chn=m+1=P艺Pnn=0+Pm-1n=mP£Pnn=0平均逗留的顾客人数为=SnPn+S(n-m)Pnn=0n=0n=mn=m平均等待时间为P+LPW——q九-pm平均逗留时间为W-LP*1

mp.G-p\卩W-Lc假设及说明通常，患者到来后，接受服务的顺序为：挂号、诊断、交费、取药。用节点1、2、3、4、一次表示挂号处、诊断处、交费处、取药处。每个节点由若干服务台并联而成，均是一个独立的服务机构，4个节点按以上顺序串联构成排队网络，因此有这个4个节点组成的排队网络可近似地描述门诊排队现象。输入过程：据观测，患者流基本满足平稳性、无后效果及普通型，因为假设患者输入流为Poisson流，单个到达，来源无限。设N(t)表示(0,t］时间内来到的患者数，现在据某大型医院门诊部的观测结果，用x2检验法对服从Poisson分布进行假设检验H:N(t)的分布律PC)—P(NQ—k}-"显e儿0kk!k=0、1、2、3…去t=1，样本容量n=160,数据如下：来到的患者数K012345发生的频数f1837154k由点估计：力-丄£kf—2.04，计算得:nkk—0k012345nPf1)k20.8042.4343.2629.4315.016.12f-nP6)1JknPf1)0.3770.9741.0501.9470.0000.734f-nP…°X2=为kk=5.028.

nPvizK=0k可见x2<x2（4），所以0.05取显著性水平可见x2<x2（4），所以0.050.05在水平0.05下接受假设H，即认为患者为Poisson流0（2）排队规则：等待制，挂号限额，先到者先服务，系统容量有限。但通常几乎不发生患者数达到限额的现象，因此认为容量近似无限。（3）服务机构：门诊排队系统为混合型网络，患者单个接受服务。现以m]表示节点1处的服务台数目，以l表示节点2处的诊断科室数，以s表示第i诊断i科室（编号）的相同服务台的，以m表示节点3出的服务台数，以r、r分别3i2表示节点4处西药房及中药房的服务台数。服务台的服务时间具有记忆性，即服从负指数分布，且每个患者的服务时间独立。排队及主要指标8.1模型分析在排队网络中，前一节点的输出流构成后裔及诶点输入流，因此每个节点的输入流均是Poisson流，每个服务台的服务时间均服从负指数分布。挂号窗口一般不同，因此节点1处的排队系统由m个M/M/1/w并联而成i每个诊断科室均为一个独立的服务系统，服务台不加区别，因此节点2处的排队系统由M/M/s/g（i=1,2,3…，l）并联而成i交费窗口不加区别，因此3处的排队系统由M/M/m/g3节点4通常分为窗口不加区别的西药房和中药房，因此节点4的排队系统由M/M/r/g和M/M/r/g并联而成。i2综上所述，此排队网络涉及两种排队模型，即M/M/1/g和M/M/m/g8.2模型的主要指标用NC）、NC）分别表示系统M/M/1/g和M/M/m/g在t时刻的患者数，则i2（N>O},（NQt>O}均是状态有限的生死过程，平稳解存在。12设患者Poisson到达的参数为九,服务时间参数为卩。下面给出两种模型的主要的稳定太指标1）M/M/1/g令服务强度为p，则p=；P=limb（t）=n}=pnP，其中p=1-p，卩nt*100n=1，2，…，则主要的稳定态指标如下：平均队长：N=£nPnn=0P1-P平均等待队长：N=艺nPn+in=1p21-p平均等待时间：谚=片N平均逗留时间：T=N；—T_W平均服务系数：F=T^WT2）M/M/m/g—令服务强度为p=上，则myP=lim（NC）=n}=n2nTgP,n<m0mmpnP,n>m、m!0其中P=0m_1（mp丄+（mp）mn!m!（1-p）n=0.主要的稳定态指标如下平均等待队长：N=艺（n-m）P=/Pmp）；n（1-p）2

n=my平均队长：N=N+—；平均等待时间：平均逗留时间：九平均逗留时间：九平均服务系数：模型中的未知参数卩、九利用抽样数据有点估计得到后，以上指标便可求得。8.3各节点的到达率假设节点1处各窗口的设制合理，以九表示患者Poisson到达的到达率，则节点1处可看成将患者流独立均匀的分到m］个M/M/1/g系统中去，使每个子Poisson流的到达率均为九二一.1m1节点1转入节点2的Poisson流参数为九，若将患者选择诊断科室i接受服务的概率记为q，则科室i的到达率为九=q九，i二1，2，・・・，l。i2ii节点3的输入流来自节点2，其参数九=£九=九.32ii=1对节点4,由于一部分患者既去西药及中药，所以若以P，P分别记患者4,14,2由节点3直接来到西药房、中药房的概率，以P，P分别表示先取西药后再1,22,1取中药和先取中药后再取西药的概率，则西药房和中药房的患者到达率分别为九=P九+PP九，九=P九+PP九.4,12,14,24,24,22,14,1这里的q（i=1，2，…，l）、P、P、P、P均可由多次观察TOC\o"1-5"\h\zi4,14,22,11,2的对应频率的平均值来近似获得。8.4网络的主要指标以N、N.、、T分别记节点i处的平均队长、平均等对长、平均iiii等待时间、平均逗留时间（i=1，2，・・・，l）；以亍、厂、、厂分2,i2,i2,i别记节点2中科室i处的平均队长、平均等对长、平均等待时间、平均逗留时

间（i二1,2,・・・，1）,分别以亍、厂、!~、厂记取药处的平均队长、TOC\o"1-5"\h\z4,i2,i2,i平均等对长、平均等待时间、平均逗留时间（i=1对应西药房，i=2对应中药房）,则整个排队网络的主要指标如下：平均队长：N=亍+N~N~；1l2,i324,ii=1i=1平均等待排队：平均等待时间：平均逗留时间：N=N亍+N~N~；平均等待排队：平均等待时间：平均逗留时间：1l2,i324,ii=1i=1~~1l~~12+-乙++—乙W；1l2,i324,ii=1i=1T=T+1工厂+T+1为T~；1l2,i324,ii=1i=1平均服务系数：最优化问题医院门诊排队系统由患者与医院两方面组成，患者一方面总希望逗留时间越短越好，因而服务台数越多，服务效率越改越好，这样，患者遭受的损失较小，但医院服务费用却增大了。因为设备的增加，服务率的提高时有条件的，因此，应从双方方的利益出发，以费用作为优化指标，进行综合考察，求出最佳的服务台数。令：总费用=排队损失费+排队费若服务水平固定，则排队损失是服务台数的减函数，服务费式服务台数目的增函数。当总费用的最小值存在时，对应的服务台数目即为最有服务台数。例如:考察系统M/M/m/g。设每个患者在系统中逗留单位时间损失费用为c1元，医院单位时间服务率成本为c元，则单位时间平均总损失费用为：2F=cN（m）+cmy，m>112用边际分析法，求最优的m*，使即m*必须满足：N(*)-NCm*+1)<鼻<NCm*-1)一NCm*)c1*…计算N(m)相邻二值之差N(m)-N(m+1)，若■落在c*1—1)NC*+1)-NC*'内，，此时病人和医院双方损失最小,则对应的m*即为最佳服务台数。10.对某一大型医院的数据研究：表1单个患者接受服务的时间观测法xi科室观测值挂号处(s)1016101620151111101018151092012容量(人)30301482069820121610202017收容处(s)567040535457133634331675736804030容量(人)443168354550423534453918303166256203533632530392567753651西药房(s)16155240701391310120301019524816容量（人）容量（人）261330345042283260182426容量（人）容量（人）261330345042283260182426中药房（s）16222791062317403075181798530容量（人）26210152050121018410901275内科（min）5899556867546344容量（人）363210343394656834456910妇科（min）23102757147657511126容量（人）305104379685915121012小儿科（min）58512965151378755146容量（人）306866712866776510口腔科（min）3032252860201823161512254259容量（人）422520302331282420283630293850301742402127304925333118表2节点1处单位时间（lmin）来到的患者数的观测值患者频数观测~~值患者数k012345678频数f183650545149302210k表3不同科室患者来到的频率观察值科室科室内科4342100169148241206658748744152149150158内科43421001691482412066587487441521491501585987477^2151551171401619617036795808^妇科221224120684788365874874495568063899775

丽亦丽妇科221224120684788365874874495568063899775

丽亦丽719961丽丽6290580丽儿科321871637824120665874874481518175776259

^5987477W^7036^7978580丽节点3转入中药房1431133312743151557迈7521116111113431171096511171756西药房转入中药房1011111112211111656543647534755112111111875746556中药房转入西药方10丄丄10011丄0丄丄0丄101056151010101000100丄001001101001010151065由表1得到平均服务率的估计值：_n|1U£x1i=1由表2得节点1处的平均到达率的估计值：

£k•fk九沁40320由表3得各平均频率作为对应概率的估计值，继而得到TOC\o"1-5"\h\z九=qX(i=1,2,3,4)2ii九=九3九二PX+PPX41321423X二PX+PPX42312423于是得到以下计算结果：表4各概率的估计值qqqqqqqq12344,24,11,22,10.20480.10370.09990.08090.2200.7800.2150.070表5各到达率、服务率、服务强度及服务台数目科室到达率服务率服务强度服务台数挂号室3.7402.0400.920

挂号室3.7402.0400.920内科0.7660.1800.8505妇科0.3880.1400.9203儿科0.3740.1500.8303口腔科0.3030.0340.89010收费处3.7401.3100.9503西药房2.9701.5400.9602中药房1.4500.8100.9002表6各科室的主要指标科室指标N/人N__/人W/minT/minF__挂号室10.611.55.76.10.07内科3.57.84.610.20.55妇科9.812.625.332.50.22儿科4.67.112.319.00.35口腔科5.114.016.846.20.64收费处29.332.27.88.60.09西药房22.224.17.58.10.07中药房7.39.15.16.30.19表7排队网络的主要指标N/人N__/人W/minT/minF__N__最大T最大60.470.734.648.90.2981.875.3结论：有结果可以看出，挂号室、收费处、西药房、排队现象严重，服务效率偏低，应增加服务台数，如挂号室增加一个窗口，平均队长就由11.5变为1.6服务系数则有0.07提升至0.39，诊断室中，妇科、口腔科患者的逗留时间长，大夫的服务强度大。在医疗设施及服务台数不变的情