辽宁省沈阳市重工第五高级中学2022-2023学年高三数学文上学期期末试卷含解析

辽宁省沈阳市重工第五高级中学2022-2023学年高三数学文上学期期末试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有是一个符合题目要求的1.已知，且，则(

)A．

B．

C．－7

D．7参考答案：C2.设P是双曲线与圆在第一象限的交点，F1，F2分别是双曲线的左，右焦点，若，则双曲线的离心率为（

）．A. B. C. D.参考答案：B【分析】先由双曲线定义与题中条件得到，，求出，，再由题意得到，即可根据勾股定理求出结果.【详解】解：根据双曲线定义：，，∴，∴，，，∴是圆的直径，∴，在中，，得．故选．【点睛】本题主要考查求双曲线的离心率，熟记双曲线的简单性质即可，属于常考题型.3.设分别为双曲线的左、右焦点，P为双曲线右支上一点，，半径为a的圆I与的延长线线段及的延长线分别切于点，则该双曲线的离心率为（）A．2

B．

C．3

D．参考答案：4.下列结论正确的是（）（A）当（B）的最小值为2

（C）当时，的最小值为（D）当时，有最大值.参考答案：D略5.设,

其中

为常数，则

A.492

B.482

C.452

D.472参考答案：A6.已知复数，则（

）A.0 B.1 C. D.2参考答案：D【分析】根据复数的运算法则，求得，再根据复数模的计算公式，即可求解．【详解】由题意复数，则，所以，故选D．【点睛】本题主要考查了复数的运算，以及复数模的计算，其中解答中熟记复数的运算法则，合理准确运算是解答的关键，着重考查了运算与求解能力，属于基础题．7.若二项式的展开式中的系数是84，则实数（

）A.2

B.

C.1

D.参考答案：C8.设是两条不同的直线，是两个不同的平面，则下列命题中正确的是（A）若且，则（B）若且，则（C）若且，则（D）若且，则参考答案：B9.是函数为奇函数的（

）．A．充分不必要条件

B．必要不充分条件

C．充要条件

D．既不充分也不必要条件参考答案：A10.设集合，，则（

）A．(－1,0)

B．(0,1)

C．(－1,3)

D．(1,3)参考答案：C二、填空题:本大题共7小题,每小题4分,共28分11.已知实数x，y满足，则的最大值为．参考答案：

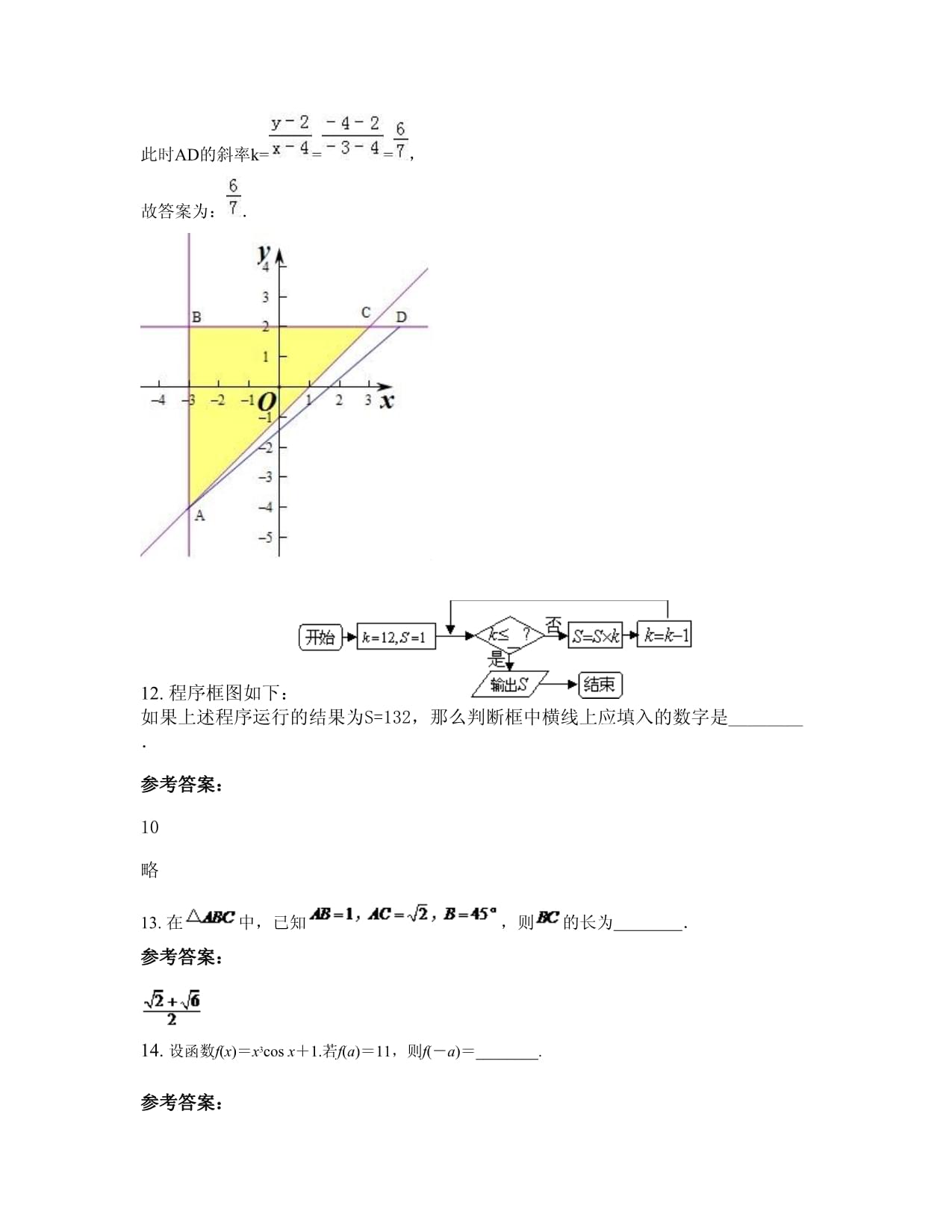
【考点】简单线性规划．【分析】作出不等式组对应的平面区域，利用斜率的几何意义进行求解即可．【解答】解：作出不等式组对应的平面区域如图：的几何意义是区域内的点到定点D（4，2）的斜率，由图象知AD的斜率最大，由得，即A（﹣3，﹣4），此时AD的斜率k===，故答案为：．12.程序框图如下：如果上述程序运行的结果为S=132，那么判断框中横线上应填入的数字是________．参考答案：10略13.在中，已知，则的长为

．参考答案：14.设函数f(x)＝x3cosx＋1.若f(a)＝11，则f(－a)＝________.参考答案：－915.函数的最大值为_______参考答案：1【分析】因为，所以可以把函数解析式化简，再逆用两角差的正弦公式化简函数解析式，利用正弦函数的性质求出最大值.【详解】,所以，因此的最大值为1.【点睛】本题考查了二角差的正弦公式的逆用，正弦型函数的最值，考查了三角恒等变换.16.设＝(1，－2)，＝(a，－1)，＝(－b,0)，a>0，b>0，O为坐标原点，

若A、B、C三点共线，则的最小值是________．参考答案：8据已知∥，又∵＝(a－1,1)，＝(－b－1,2)，∴2(a－1)－(－b－1)＝0，∴2a＋b＝1，∴＋＝＋＝4＋＋≥4＋2＝8，当且仅当＝，a＝，b＝时取等号，∴＋的最小值是8.17.将正整数12分解成两个正整数的乘积有，，三种，其中是这三种分解中，两数差的绝对值最小的，我们称为12的最佳分解．当是正整数的最佳分解时，我们规定函数，例如.关于函数有下列叙述：①，②，③，④.其中正确的序号为

（填入所有正确的序号）．参考答案：①③略三、解答题：本大题共5小题，共72分。解答应写出文字说明，证明过程或演算步骤18.已知数列{an}的前n项和为Sn，且满足a1=，an=﹣2Sn?Sn﹣1（n≥2且n∈N*）．（Ⅰ）求证：数列{}是等差数列；

（Ⅱ）求Sn和an．参考答案：考点：数列递推式；等差关系的确定．专题：等差数列与等比数列．分析：（Ⅰ）由数列递推式结合an=Sn﹣Sn﹣1可得，即可说明数列{}是等差数列；（Ⅱ）由数列{}是等差数列求其通项公式，进一步得到．然后由当n≥2时，求得数列的通项公式．解答： （Ⅰ）证明：当n≥2时，an=Sn﹣Sn﹣1=﹣2SnSn﹣1，①∴Sn（1+2Sn﹣1）=Sn﹣1，由上式知若Sn﹣1≠0，则Sn≠0．∵S1=a1≠0，由递推关系知，∴由①式可得：当n≥2时，．∴{}是等差数列，其中首项为，公差为2；（Ⅱ）解：∵，∴．当n≥2时，，当n=1时，不适合上式，∴点评：本题考查了数列递推式，考查了等差关系的确定，训练了由数列的前n项和求数列的通项公式，是中档题．19.已知：，为常数）若，求的最小正周期；若在上的最大值与最小值之和为3，求的值．参考答案：（1）；（2）试题分析：（1）利用两角和正弦公式和降幂公式化简，得到的形式，利用公式计算周期．（2）求三角函数的最小正周期一般化成，，形式，利用周期公式即可,运用公式时要注意审查公式成立的条件，要注意和差、倍角的相对性，要注意升幂、降幂的灵活运用；（3）重视三角函数的三变：三变指变角、变名、变式；变角：对角的分拆要尽可能化成同名、同角、特殊角；变名：尽可能减少函数名称；变式：对式子变形一般要尽可能有理化、整式化、降低次数等，适当选择公式进行变形．试题解析：解：

（1）最小正周期（2）

即

考点：1、求三角函数的周期；2、求三角函数在闭区间上的最值．20.设点到坐标原点的距离和它到直线的距离之比是一个常数．（1）求点的轨迹；（2）若时得到的曲线是，将曲线向左平移一个单位长度后得到曲线，过点的直线与曲线交于不同的两点，过的直线分别交曲线于点，设，，，求的取值范围．参考答案：（Ⅰ）见解析;（Ⅱ）.试题分析:(1)设，直接法求出点的轨迹方程，由轨迹方程判断出轨迹;(2)由已知条件求出曲线E的方程,利用向量坐标运算求出,设直线的斜率为,联立直线的方程和曲线E的方程,利用韦达定理求出,再求出的范围.试题解析:（Ⅰ）过点作，为垂足，设点的坐标为，则，又，所以，故点的轨迹方程为.可化为，显然点的轨迹为焦点在轴上的椭圆.（Ⅱ）时，得到的曲线的方程是，故曲线的方程是.设,，则，由，得，即.

当与轴不垂直时，直线的方程为，即，代入曲线的方程并注意到，整理可得，则，即，于是.当与轴垂直时，A点的横坐标为，，显然也成立.同理可得.

设直线的方程为，联立，消去y整理得，由及，解得.又，则.故求的取值范围是.点睛:本题考查了轨迹方程的求法以及直线与椭圆相交时相关问题,属于中档题.在(1)中,求轨迹与求轨迹方程不一样,把轨迹方程求出来后,再判断是什么类型的曲线;在(2)中,注意向量坐标运算求出的表达式,再联立直线的方程和椭圆方程求出,进而求出的范围.21.（本小题满分13分）已知等差数列前三项的和为，前三项的积为.（Ⅰ）求等差数列的通项公式；（Ⅱ）若，，成等比数列，求数列的前项和.参考答案：解：（Ⅰ）设等差数列的公差为，则，，由题意得

…2分解得或

…4分

所以由等差数列通项公式可得，或.故，或.

…6分（Ⅱ）当时，，，分别为，，，不成等比数列；…7分当时，，，分别为，，，成等比数列，满足条件.故

…9分

记数列的前项和为.当时，；当时，；当时，

.当时，满足此式.…12分综上，

…13分22.如图，A、B、C、D四点在同一圆上，AD的延长线与BC的延长线交于E点，且EC=ED．（Ⅰ）证明：CD∥AB；（Ⅱ）延长CD到F，延长DC到G，使得EF=EG，证明：A、B、G、F四点共圆．参考答案：【考点】圆內接多边形的性质与判定．【专题】证明题．【分析】（I）根据两条边相等，得到等腰三角形的两个底角相等，根据四点共圆，得到四边形的一个外角等于不相邻的一个内角，高考等量代换得到两个角相等，根据根据同位角相等两直线平行，得到结论．（II）根据第一问做出的边和角之间的关系，得到两个三角形全等，根据全等三角形的对应角相等，根据平行的性质定理，等量代换，得到四边形的一对对角相等，得到四点共圆．【解答】解：（I）因为EC=ED，所以∠EDC=∠ECD因为A，B，C，D四点在同一圆上，所以∠EDC=∠EBA故∠ECD=∠E