角的概念的推广二

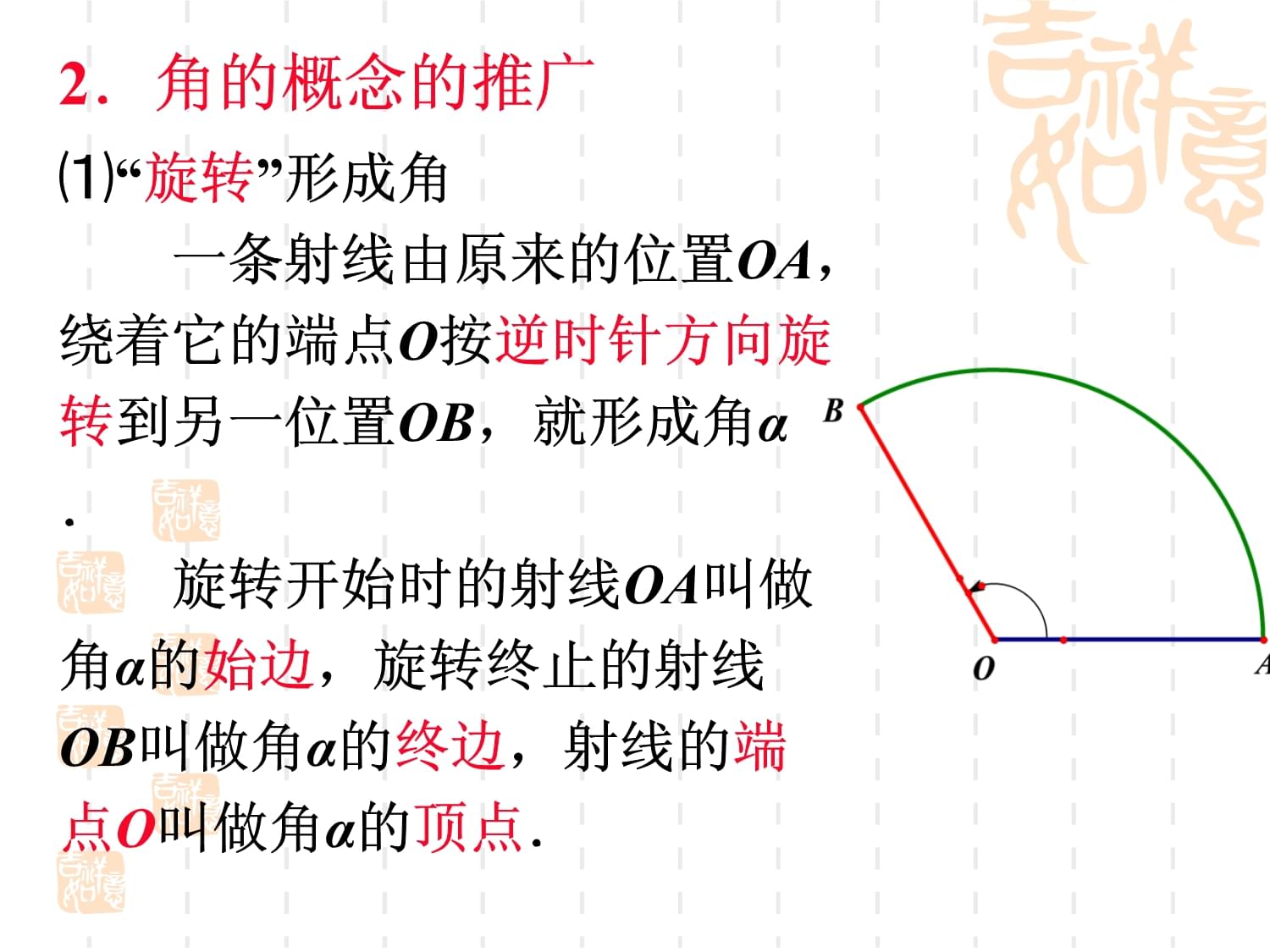
1.1.1角的概念的推广1、角的概念初中是如何定义角的？从一个点出发引出的两条射线构成的几何图形.这种概念的优点是形象、直观、容易理解，但它是从图形形状来定义角，因此角的范围是[0º,360º)，这种定义称为静态定义，其弊端在于“狭隘”.2．角的概念的推广⑴“旋转”形成角一条射线由原来的位置OA，绕着它的端点O按逆时针方向旋转到另一位置OB，就形成角α．旋转开始时的射线OA叫做角α的始边，旋转终止的射线OB叫做角α的终边，射线的端点O叫做角α的顶点．⑵．“正角”与“负角”、“0º角”我们把按逆时针方向旋转所形成的角叫做正角，把按顺时针方向旋转所形成的角叫做负角，如图，以OA为始边的角α=210°，β=－150°，γ=660°，特别地，当一条射线没有作任何旋转时，我们也认为这时形成了一个角，并把这个角叫做零度角（0º）．角的记法：角α或可以简记成∠α特别地，当一条射线没有作任何旋转时，我们也认为这时形成了一个角，并把这个角叫做零度角（0º）．角的记法：角α或可以简记成∠α.⑶角的概念扩展的意义：用“旋转”定义角之后，角的范围大大地扩大了①角有正负之分; 如：=210,

=150,

=660.②角可以任意大; 实例：体操动作：旋转2周（360×2=720）3周（360×3=1080）③还有零角,一条射线，没有旋转.角的概念推广以后，它包括任意大小的正角、负角和零角．要注意，正角和负角是表示具有相反意义的旋转量，它的正负规定纯属于习惯，就好象与正数、负数的规定一样，零角无正负，就好象数零无正负一样．用旋转来描述角，需要注意三个要素（旋转中心、旋转方向和旋转量）（2）旋转方向：旋转变换的方向分为逆时针和顺时针两种，这是一对意义相反的量，根据以往的经验，我们可以把一对意义相反的量用正负数来表示，那么许多问题就可以解决了；（1）旋转中心：作为角的顶点.（3）旋转量：当旋转超过一周时，旋转量即超过360º，角度的绝对值可大于360º.于是就会出现720º，－540º等角度.3．“象限角”为了研究方便，我们往往在平面直角坐标系中来讨论角。角的顶点重合于坐标原点，角的始边重合于x轴的正半轴，这样一来，角的终边落在第几象限，我们就说这个角是第几象限的角（角的终边落在坐标轴上，则此角不属于任何一个象限）例如：30、390、330是第Ⅰ象限角，300、60是第Ⅳ象限角，585、1300是第Ⅲ象限角，135、2000是第Ⅱ象限角等4．终边相同的角角⑴观察：390，330角，它们的终终边都与30角的终边相同同.⑵探究：终边相同的角角都可以表示示成一个0到360的角与k(k∈Z)个周角角的和：390=30+360(k=1),330=30360(k=－1)30=30+0×360(k=0),1470=30+4×360(k=4)1770=305×360(k=－5)⑶结论：：所有与终边相同的角角连同在内可以构成成一个集合：{β|β=α+k·360º}(k∈Z)即：任何一个个与角终边相同的角角，都可以表表示成角与整数个周角角的和⑷注意以下四四点：①k∈Z；②是任意角；③k·360º与之间是“+”号，如k·360º－30º,应看看成k·360º+(－30º)；④终边相同的角角不一定相等等；相等的角，终终边一定相同同；终边相同的角角有无数多个个，它们相差差360º的的整数倍.例1.在0º到360º范围内内，找出与下下列各角终边边相同的角，，并判断它是是哪个象限的的角.(1)－120º；(2)640º；(3)－950º12′.解：⑴∵－120º=－360º+240º，∴240º的的角与－120º的角终终边相同，它是第三象限限角．⑵∵640º=360º+280º，∴280º的的角与640º的角终边边相同，它是第四象限限角．⑶∵－950º12’=－3××360º+129º48’，∴129º48’的角与与－950ºº12’的角角终边相同，，它是第二象限限角．例2.写出终边落在在Y轴上的角角的集合。终边落在坐标标轴上的情形形xyo0090018002700+Kx3600+Kx3600+Kx3600+Kx3600或3600＋KX3600例2.写出终边落在在y轴上的角的集集合。解：终边落在ｙ轴轴正半轴上的角的的集合为S1={β|β=900+K∙3600,K∈Z}={β|β=900+2K∙1800,K∈Z}={β|β=900+1800的偶数倍}终边落落在ｙｙ轴负半轴上上的角角的集集合为为S2={β|β=2700+K∙∙3600,K∈∈Z}={β|β=900+1800+2K∙1800,K∈∈Z}={β|β=900+（2K+1）1800，K∈Z}={β|β=900+1800的奇数倍}S=S1∪S2所以，，终边边落在在ｙ轴上的角角的集集合为为={β|β=900+1800的偶数倍}∪{β|β=900+1800的奇数倍}={β|β=900+1800的整数倍}={β|β=900+K∙1800，K∈Z}｛偶数数｝∪｛奇数数｝＝｛整整数｝｝XYO900+K∙36002700+k∙3600变式1：分别写出终终边落落在ｘ轴正半轴轴上、在ｘ轴轴负半半轴上、在在y轴轴正半半轴上上、在在y轴轴负半半轴上上、在在ｘ轴轴上、、在y轴上上、坐坐标轴轴上的角的的集合合.变式2：写出出终边边落在在直线线y=x上的角角的集集合.变式4：分别写出终终边落落在第第一、二、、三、、四、、一三三、二二四象限的的角的的集合合.变式3：写出出终边边落在在直线线y=-x上的角角的集集合.变式3：写出终边落在直线

上的角的集合.写出终终边落落在轴轴上的的角的的集合合。解：终边边落在在轴轴正半轴上上的角角的集集合为为S1={β|β=K∙3600,K∈Z}={β|β=2K∙1800,K∈Z}={β|β=1800的偶数倍}终边落落在轴轴负半轴上上的角角的集集合为为S2={β|β=K∙3600,K∈∈Z}={β|β=2K∙1800,K∈∈Z}={β|β=（（2K+1）1800，K∈Z}={β|β=1800的奇数倍}S=S1∪S2所以终终边边落在在轴上的角角的集集合为为={β|β=1800的偶数倍}∪{β|β=1800的奇数倍}={β|β=1800的整数数倍}={β|β=K∙1800，K∈Z}｛偶数数｝∪｛奇数数｝＝｛整整数｝｝XYOK∙36001800+k∙3600yxyxyx900+900+900+2700+900+1800+900+900+1800+例21800+yx例3.写出与与下列列各角角终边边相同同的角角的集集合S，并并把S中在在－360º~720ºº间的的角写写出来来：(1)60ºº；(2)－－21º；；(3)363ºº14′.解：(1)S={β|β=k··360º+60º(k∈Z)},S中在－－360ºº～720º间间的角角是－1××360ºº+60ºº=－－300ºº；0×360º+60º=60º；；1×360º+60º=420ºº．(2)S={β|β=k··360º－－21º(k∈Z)}S中在－－360ºº～720º间间的角角是0×360º－－21º=－21ºº；1×360º－－21º=339ºº；2×360º－－21º=699ºº．(3)β|β=k··360º+363º14’’(k∈Z)}S中在在－360º～～720ºº间的的角是是－2××360ºº+363º14’’=－－356ºº46’；；－1××360ºº+363º14’’=3º14’’；0×360º+363ºº14’=363ºº14’．．知识识拓拓展展讨论：若是第二象限角时,则2，分别是第几象限的角？1.若若是是第第二二象象限限的的角角，，则则/2是是（（））A第第一一或或第第三三象象限限B第第二二或或第第三三象象限限C第第三三或或第第四四象象限限D第第一一或或第第四四象象限限A√√√小结结：：1.任任意意角角的的概概念念正角角：：射射线线按按逆时针针方方向向旋旋转转形成成的的角角负角角：：射射线线按按顺时针针方方向向旋旋转转形形成成的的角角零角角：：射射线线不作旋旋转转形形成成的的角角1)置置角角的的顶顶点点于于原点2)始始边边重重合合于于X轴轴的的正半轴轴2.象象限限角角终边边落在在第几几象象限限就是是第几几象象限限角角3.终终边边与与角角ａａ相相同同的的角角ａ＋K××3600，K∈Z作业业：：P9习习题题1.1第1题题，，第第3题题的的（（2））（（4））（（6））课堂堂练练习习1、锐角角是是第第几几象象限限的的角角？？第第一一象象限限的的角角是是否否都都是是锐锐角角？？小小于于90ºº的的角角是是锐锐角角吗吗？？区区间间(0ºº,90ºº)内内的的角角是是锐锐角角吗吗？？答：：锐锐角角是是第第一一象象限限角角；；第第一一象象限限角角不不一一定定是是锐锐角角；；小小于于90ºº的的角角可可能能是是零零角角或或负负角角，，故故它它不不一一定定是是锐锐角角；；区区间间(0ºº,90ºº)内内的的角角是是锐锐角角．．2、已知知角角的的顶顶点点与与坐坐标标系系原原点点重重合合，，始始边边落落在在x轴的的正正半半轴轴上上，，作作出出下下列列各各角角，，并并指指出出它它们们是是哪哪个个象象限限的的角角？？(1)420ºº，，(2)－－75ºº，，(3)855ºº，，(4)－－510ºº．．答：：(1)第第一一象象限限角角；；(2)第第四四象象限限角角，，(3)第第二二象象限限角角，，(4)第三三象限限角.3、已已知α,β角的终终边相相同，，那么么α－β的终边边在（（））Ax轴的非非负半半轴上上By轴的非非负半半轴上上Cx轴的非非正半半轴上上Dy轴的非非正半半轴上上A4、终终边与与坐标标轴重重合的的角的的集合合是（（））A{β|β=k··360º(k∈Z)}B{β|β=k··180º(k∈Z)}C{β|β=k··90ºº(k∈Z)}D{β|β=k··180º+90º(k∈Z)}C5、、已知知角2α的终边边在x轴的上上方，，那么么α是()A第第一一象限限角B