第五章弯曲内力.

1、5.1梁的平面弯曲的概念和计算简图梁的平面弯曲的概念和计算简图5.2梁的内力梁的内力剪力和弯矩剪力和弯矩5.3用内力方程法绘制梁的剪力图和弯矩图用内力方程法绘制梁的剪力图和弯矩图5.4用微分关系法绘制梁的剪力图和弯矩图用微分关系法绘制梁的剪力图和弯矩图5.5用区段叠加法绘制弯矩图用区段叠加法绘制弯矩图6.1梁的平面弯曲的概念及梁的计算简图梁的平面弯曲的概念及梁的计算简图一、工程实例及弯曲的概念一、工程实例及弯曲的概念桥梁、楼板梁、火车轴、挡土墙、挡水墙桥梁、楼板梁、火车轴、挡土墙、挡水墙1、弯曲：在垂直于杆轴线的平衡力系的作用下，杆的轴线在变形后、弯曲：在垂直于杆轴线的平衡力系的作用下，杆的轴

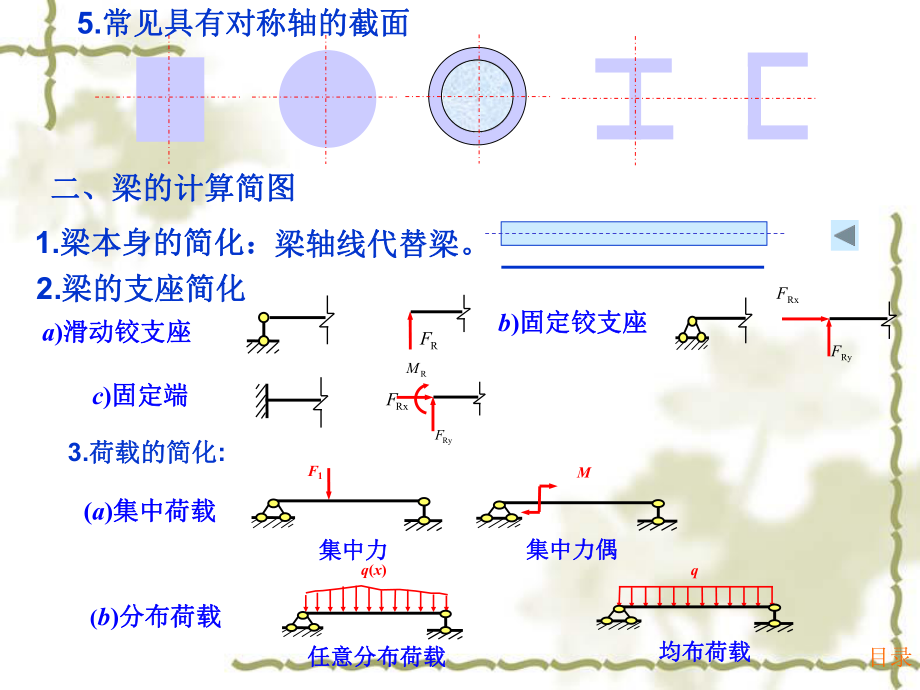
2、线在变形后成为曲线的变形形式。成为曲线的变形形式。 2、梁：以弯曲变形为主要变形的构件，通常称为梁。梁：以弯曲变形为主要变形的构件，通常称为梁。3、平面弯曲（对称弯曲）：若梁上所有外力都作用在纵向对称、平面弯曲（对称弯曲）：若梁上所有外力都作用在纵向对称面内，梁变形后轴线形成的曲线也在该平面内的弯曲。面内，梁变形后轴线形成的曲线也在该平面内的弯曲。FBFAFq纵向对称面纵向对称面4、非对称弯曲：若梁不具有纵向对称面，或梁有纵向对称面上但外力并、非对称弯曲：若梁不具有纵向对称面，或梁有纵向对称面上但外力并不作用在纵向对称面内的弯曲。不作用在纵向对称面内的弯曲。目录5.常见具有对称轴的截面常见具有

3、对称轴的截面二、梁的计算简图二、梁的计算简图 1.梁本身的简化：梁本身的简化：梁轴线代替梁。梁轴线代替梁。 2.梁的支座简化梁的支座简化a)滑动铰支座滑动铰支座b)固定铰支座固定铰支座c)固定端固定端RFRyFRxFRyFRxFRM3.荷载的简化荷载的简化:(a)集中荷载集中荷载F1集中力集中力M集中力偶集中力偶(b)分布荷载分布荷载q(x)任意分布荷载任意分布荷载q均布荷载均布荷载目录三、静定梁的分类三、静定梁的分类(a)悬臂梁悬臂梁(b)简支梁简支梁(c)外伸梁外伸梁5.2梁的内力梁的内力剪力和弯矩剪力和弯矩一、梁的剪力和弯矩FABaxAFACxSFM0yFxFMxFMMAAC0:0BFF

4、CSFMBABSBSy0:0FFFFFFFFxFxlFxFMxlFxFMMABBC0:0AFBFASSAFFFF0 剪力剪力-正负号规定：使梁有左上右下错动趋势的剪力为正，反之正负号规定：使梁有左上右下错动趋势的剪力为正，反之为负为负(左截面上的剪力向上为正，右截面上的剪力向下为正左截面上的剪力向上为正，右截面上的剪力向下为正)；或绕截面内；或绕截面内一点顺时旋转的剪力为正（反之为负）一点顺时旋转的剪力为正（反之为负） FSFSFSFS剪力为正剪力为正剪力为负剪力为负 弯矩弯矩M正负号规定：使梁变形呈上凹下凸的弯矩为正，反之为负正负号规定：使梁变形呈上凹下凸的弯矩为正，反之为负(梁上梁上压下拉

5、的弯矩为正压下拉的弯矩为正)。MMMM弯矩为正弯矩为正弯矩为负弯矩为负目录目录例例1 求下图所示简支梁求下图所示简支梁1-1与与2-2截面的剪力和弯矩。截面的剪力和弯矩。3mq=12kN/m2112BF=8kN1.5m1.5mAFAFBF=8kNFAS1F1MFBS2F2Mq=12kN/m解：解： 1、求支反力、求支反力02335 . 460qFFMABkN15AF030yqFFFFBAkN29BF2、计算、计算1-1截面的内力截面的内力kN7A1SFFFmkN5 .225 . 1A1 FM3、计算、计算2-2截面的内力截面的内力kN73B2SFqFmkN332333B2qFM由截面法得内力结

6、论由截面法得内力结论 梁任意截面上的剪力等于截面一侧梁梁任意截面上的剪力等于截面一侧梁上所有横向外力的代数和。左侧梁上向上上所有横向外力的代数和。左侧梁上向上的外力为正的外力为正(右侧梁上向下的外力为正右侧梁上向下的外力为正)，反之为负。反之为负。 梁任意截面上的弯矩等于截面一侧梁任意截面上的弯矩等于截面一侧梁上所有外力对截面形心取矩的代数和。梁上所有外力对截面形心取矩的代数和。左侧梁上顺时旋转的弯矩为正左侧梁上顺时旋转的弯矩为正(右侧梁右侧梁上逆时旋转弯矩为正上逆时旋转弯矩为正)，反之为负。，反之为负。 目录 例例2：已知：已知F=5kN，M=2kNm，q=1kN/m。试求悬臂梁试求悬臂梁1

7、1、22、33、4-4截面截面 上的内力。上的内力。M44331122ABaFaaq1kN1sF6kN2sF7kN3sF7kN4sFmkN5 . 01MmkN5 . 02Mm7kN3Mm9kN4M 5.3 用内力方程法绘制剪力图和弯矩用内力方程法绘制剪力图和弯矩1.剪力、弯矩方程剪力、弯矩方程 )()(SSxMMxFF剪力、弯矩方程的图形，横轴沿轴线方向表示截剪力、弯矩方程的图形，横轴沿轴线方向表示截面的位置，纵轴为内力的大小。面的位置，纵轴为内力的大小。 2.剪力、弯矩图：剪力、弯矩图：目录例例3 图示简支梁受均布荷载图示简支梁受均布荷载q的作用，作该梁的剪力图和弯矩图。的作用，作该梁的剪力

8、图和弯矩图。解解 （1）求支座反力）求支座反力 FBFAqlAB0AM0BM2 qlFFBA （2）列剪力方程和弯矩方程）列剪力方程和弯矩方程qxqlqxFxFAS2)(22222)(xqxqlxqxFxMA(0 xl)（0 xl） 2maxqlFS82qlMmax2ql2ql82ql目录FabClABxFAFBlFb /lFa /FSlFab /M例例4 作简支梁的内力图作简支梁的内力图 lFbFBlFaFAlFbFxFAS)(xlFbxFxMA)(（0 xa） （0 xa）解解 （1）求支座反力）求支座反力（2）列剪力方程和弯矩方程）列剪力方程和弯矩方程AC段段： lFaFFxFAS)()

9、()()(xllFaxlFxMBlFaFSmaxlFabMmaxCB段：段： （axl）（axl）（3）绘剪力图和弯矩图由剪力、弯矩图知：由剪力、弯矩图知：在集中力作用点，弯矩图发生转在集中力作用点，弯矩图发生转折，剪力图发生突变，其突变值等于集中力的大小，折，剪力图发生突变，其突变值等于集中力的大小，从左向右作图，突变方向沿集中力作用的方向从左向右作图，突变方向沿集中力作用的方向。目录例例5 在图示简支梁在图示简支梁AB的的C点处作用一集中力偶点处作用一集中力偶M，作该梁的剪，作该梁的剪力图和弯矩图。力图和弯矩图。 abClABMFSlM /MlMa/lMb/解解 （1）求支座反力）求支座反

10、力 lMFFBA（2）列剪力方程和弯矩方程）列剪力方程和弯矩方程AC段：段：lMFxFAS)(xlMxFxMA)( （0 xa） （0 xa）CB段：段： lMFxFBS)(（axl）)()()(xllMxlFxMB (axl)（3）绘剪力图和弯矩图）绘剪力图和弯矩图lMaMmax由剪力、弯矩图知：由剪力、弯矩图知：在集中力偶作用点，弯矩图发生突变，在集中力偶作用点，弯矩图发生突变，其突变值为集中力偶的大小。其突变值为集中力偶的大小。 目录ABxFFFlMFxxMFxF)()(SFlMFFmaxmaxS|例例6 作图示悬臂梁作图示悬臂梁AB的剪力图和弯矩图。的剪力图和弯矩图。剪力、弯矩方程：目

11、录梁上集中荷载及支座处内力有以下特点梁上集中荷载及支座处内力有以下特点（1）集中力作用处，剪力无定值，定突变，变化的大小就）集中力作用处，剪力无定值，定突变，变化的大小就是该处集中力的数值。当该处集中力向上作用时，从左邻是该处集中力的数值。当该处集中力向上作用时，从左邻到右邻剪力的数值增加。到右邻剪力的数值增加。当该处集中力向下作用时，从左邻到右邻剪力的数值减小。当该处集中力向下作用时，从左邻到右邻剪力的数值减小。（2）集中力偶作用处，弯矩无定值，定突变，变化的大小）集中力偶作用处，弯矩无定值，定突变，变化的大小就是该处集中力偶的数值。当该集中力偶顺时转时，从左邻就是该处集中力偶的数值。当该集

12、中力偶顺时转时，从左邻到右邻弯矩的数值增加。当该集中力偶逆时转时，从左邻到到右邻弯矩的数值增加。当该集中力偶逆时转时，从左邻到右邻弯矩的数值减小。右邻弯矩的数值减小。（3）在两端的铰处或自由端，只要该处无集中力偶，则两）在两端的铰处或自由端，只要该处无集中力偶，则两端内侧截面的端内侧截面的M=0。若该处有集中力偶。若该处有集中力偶Me作用，则梁端内作用，则梁端内侧面或自由端内侧面侧面或自由端内侧面M=Me(4)最大弯矩可能发生在最大弯矩可能发生在 a)集中力作用处集中力作用处 b)集中力偶作用处集中力偶作用处 c)Fs=0处处 d)固定端固定端目录5.4用微分关系法绘制梁的剪力图和弯矩图用微分

13、关系法绘制梁的剪力图和弯矩图一一、剪力、弯矩和分布载荷间的微分关系、剪力、弯矩和分布载荷间的微分关系xMF1q(x)AByxdxFS(x)dxM(x)M(x)+dM(x)FS(x)+dFS(x)q(x)O：0OM0)(21)()()(d)(2SdxxqdxxFxMxMxM)(d)(dSxFxxM 0Y)(d)(dSxqxxF0)()(d)()(SSSdxxqxFxFxF)(d)(d22xqxxM目录二二、讨论微分关系的几何意义、讨论微分关系的几何意义1.微分关系的几何意义：微分关系的几何意义：)()(SxqdxxdF 剪力图上某点处的切线斜率等于该点处荷载剪力图上某点处的切线斜率等于该点处荷载

14、 )()(SxFdxxdM弯矩图上某点处的切线斜率等于该点剪力的大小。弯矩图上某点处的切线斜率等于该点剪力的大小。 )()(22xqdxxdM弯矩图上某点处的切线斜率的变化率等于该点载集度的大小弯矩图上某点处的切线斜率的变化率等于该点载集度的大小 。 2.各种荷载下剪力图与弯矩图的形态：各种荷载下剪力图与弯矩图的形态： 外力情况外力情况q0(向下向下)无荷载段无荷载段集中力集中力F作用处：作用处：集中力偶集中力偶M作用处：作用处：剪 力 图 上剪 力 图 上的特征的特征(向下斜直向下斜直线线)水平线水平线突 变突 变 ， 突突变值为变值为F不变不变弯 矩 图 上弯 矩 图 上的特征的特征(下凸

15、抛物线下凸抛物线) 斜直线斜直线有有尖点尖点有有突变突变，突突变值为变值为M最 大 弯 矩最 大 弯 矩可可 能的截能的截面位置面位置剪力为零的剪力为零的截面截面剪 力 突 变剪 力 突 变的截面的截面弯矩突变的弯矩突变的某一侧某一侧目录三、弯矩、剪力与分布荷载集度之间的积分关系及几何意义三、弯矩、剪力与分布荷载集度之间的积分关系及几何意义BAXXBASxxqxFd)()(dBAXXSASBxxqFFd)( 式中：式中：FSA 、FSB分别表示分别表示A、B两个横截面上的剪力。两个横截面上的剪力。任何两个截面上的剪力之差，等于这两个截面间梁段上的荷载任何两个截面上的剪力之差，等于这两个截面间梁

16、段上的荷载 图的面积。图的面积。几何意义几何意义：xxFMMBAXXSABd)( 式中：式中：MA、MB分别表示分别表示A、B两个横截面上的弯矩。两个横截面上的弯矩。几何意义几何意义： 任何两个截面上的弯矩之差，等于这两个截面间的剪力图的面积。任何两个截面上的弯矩之差，等于这两个截面间的剪力图的面积。 四、利用微分关系作剪力弯矩图四、利用微分关系作剪力弯矩图1.先利用计算法则计算分段点先利用计算法则计算分段点FS、M值；值；2.利用微分关系判断并画出分段点之间的利用微分关系判断并画出分段点之间的FS、M图图目录kN8 . 3kN2 . 7BAFF例例7 、外伸梁、外伸梁AB承受荷载如图所示，承

17、受荷载如图所示，作该梁的作该梁的FS-M图。图。解：解： 1、求支反力、求支反力DABm1m4m1kN3kN/m2mkN6C(kN)FS3.8Ex=3.1m4.231.413.832.2(kNm)M2、分段定端值、分段定端值CADBFS-3kN-3kN4.2kN-3.8kN-3.8kN-3.8kNM0-3kNm-3kNm-2.2kNm3.8kNm03、据荷载分布情况逐段绘出梁的剪力、据荷载分布情况逐段绘出梁的剪力图和弯矩图图和弯矩图目录5.5用区段叠加法绘制弯矩图用区段叠加法绘制弯矩图叠加原理：由几个外力所引起的某一参数值（内力、应力、位移等），由几个外力所引起的某一参数值（内力、应力、位移等

18、），等于每个外力单独作用时所引起的该参数值之总和。等于每个外力单独作用时所引起的该参数值之总和。注意：叠加原理只有在参数与外力成线性关系时才能成立。注意：叠加原理只有在参数与外力成线性关系时才能成立。 例例8、如图简支梁，受分布荷载、如图简支梁，受分布荷载q和和MA、MB作用，用叠加法绘出其弯矩图作用，用叠加法绘出其弯矩图qABMBMAlMBMAM1M2MMBMA82qlM 82ql注意注意：这里所说的弯矩叠加，这里所说的弯矩叠加，是纵坐标的叠加而不是指图形的拚合。是纵坐标的叠加而不是指图形的拚合。目录区段叠加法作弯矩图区段叠加法作弯矩图对梁进行分段，再在每一个区段上利用叠加原理进行弯矩图的叠

19、加，对梁进行分段，再在每一个区段上利用叠加原理进行弯矩图的叠加，这样更方便实用，这种方法通常称为区段叠加法。这样更方便实用，这种方法通常称为区段叠加法。例例9、 做如图所示梁的剪力和弯矩图做如图所示梁的剪力和弯矩图BMlAMqABFABCqlDFSAMBFSBMAABqMBMAMBMA目录例例10、做如图所示梁的剪力和弯矩图、做如图所示梁的剪力和弯矩图 CABFS-20kN-20kN15kN-25kNM0-20kNm20kNm0m40kNmkN20kN/m10qCAB1m4mYAYB152025202031.25kN35AYkN25BYkN25maxSFmkN25.31maxMFSM目录例例11、 利用剪力、弯矩与荷载集度的关系作图所示梁的剪力利用剪力、弯矩与荷载集度的关系作图所示梁的剪力图和弯矩图。图和弯矩图。qCABaYAYBqa22qa4qa4qa43qa322qa322qa42qa42qa4qaYA4qaYB43qamaxSF42ma