大学物理_物理学_课件_振动与波动

1、1第七章第七章振动与波动振动与波动2 一般地说一般地说,任何一个物理量在某一量值附近随时间任何一个物理量在某一量值附近随时间作周期性变化都可以称为作周期性变化都可以称为振动振动。 振动有机械振动、电磁振动、光振动振动有机械振动、电磁振动、光振动.。 本章着重研究本章着重研究机械振动机械振动。物体在一定的位置附近。物体在一定的位置附近作往返运动，称为作往返运动，称为机械振动。机械振动。 振动中最简单最基本最有代表性的是振动中最简单最基本最有代表性的是简谐振动简谐振动。 振动的传播就是振动的传播就是波波。在弹性介质中发生的波动，。在弹性介质中发生的波动，是依靠弹性介质质点的机械振动而产生和传播的，

2、因是依靠弹性介质质点的机械振动而产生和传播的，因而称为而称为机械波机械波，或，或弹性波弹性波。 并不是所有的波都依靠介质传播并不是所有的波都依靠介质传播，光波、无线，光波、无线电波可以在真空中传播，称为电波可以在真空中传播，称为电磁波电磁波。微观粒子也。微观粒子也有波动性，这种波称为有波动性，这种波称为实物波实物波或或德布罗意波德布罗意波。3一一 . .简谐振动的基本特征简谐振动的基本特征研究简谐运动的意义研究简谐运动的意义在一切振动中，最简单和最基本的振动称为简谐振动在一切振动中，最简单和最基本的振动称为简谐振动任何复杂的运动都可以看成是若干简谐振动的合成任何复杂的运动都可以看成是若干简谐振

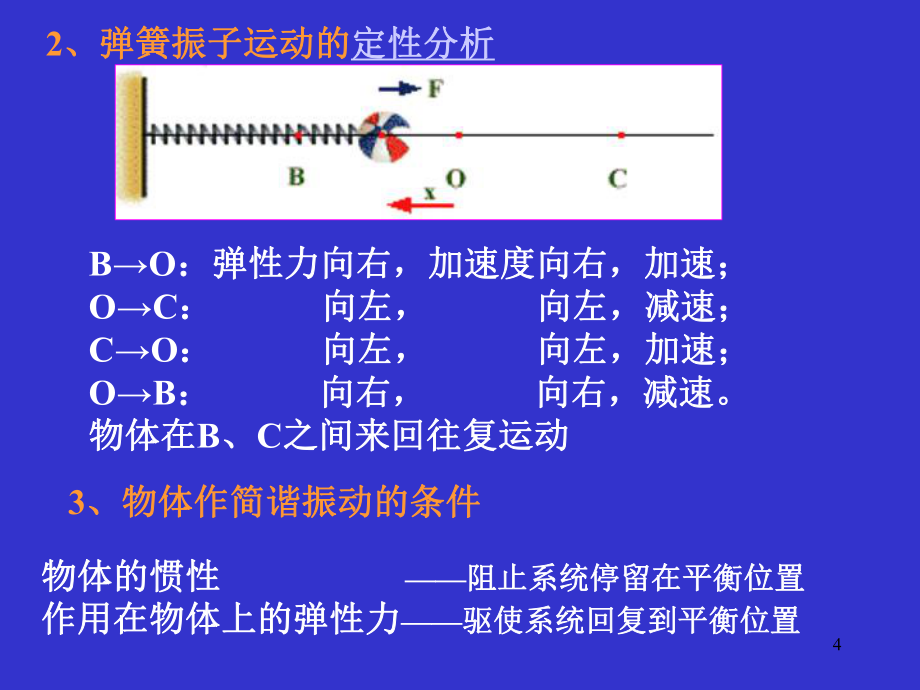
3、动的合成1、以弹簧振子为例、以弹簧振子为例O O点为小球水平方向不受力的位置，称为点为小球水平方向不受力的位置，称为平衡位置平衡位置。42、弹簧振子运动的、弹簧振子运动的定性分析定性分析BO：弹性力向右，加速度向右，加速；：弹性力向右，加速度向右，加速；OC： 向左，向左， 向左，减速；向左，减速；CO： 向左，向左， 向左，加速；向左，加速；OB： 向右，向右， 向右，减速。向右，减速。物体在物体在B、C之间来回往复运动之间来回往复运动3、物体作简谐振动的条件、物体作简谐振动的条件物体的惯性物体的惯性 阻止系统停留在平衡位置阻止系统停留在平衡位置作用在物体上的弹性力作用在物体上的弹性力驱使系

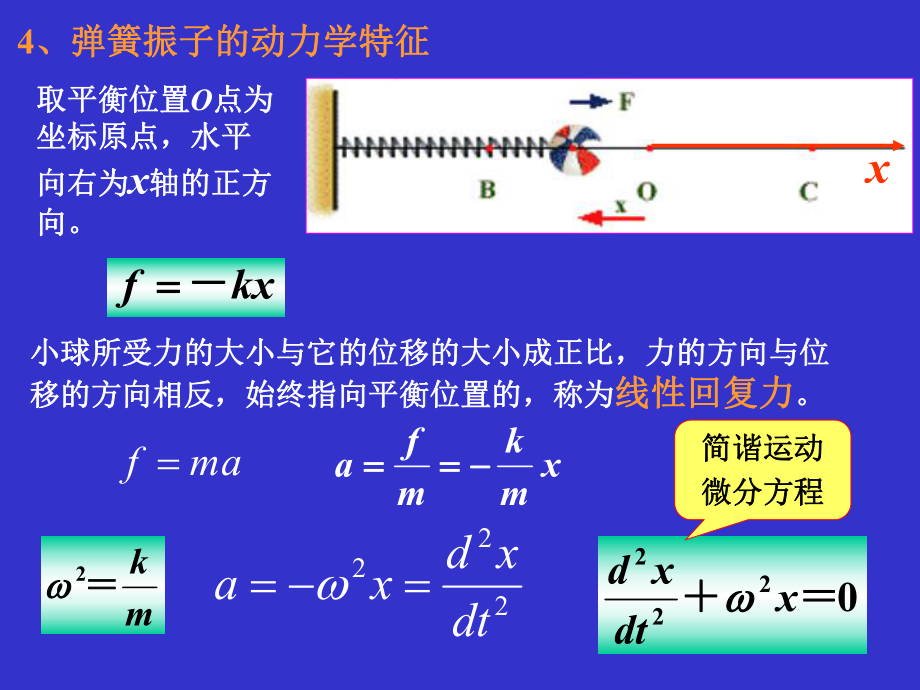
4、统回复到平衡位置驱使系统回复到平衡位置54、弹簧振子的动力学特征、弹簧振子的动力学特征取平衡位置取平衡位置O点为点为坐标原点，水平坐标原点，水平向右为向右为x轴的正方轴的正方向。向。xkxf 小球所受力的大小与它的位移的大小成正比，力的方向与位小球所受力的大小与它的位移的大小成正比，力的方向与位移的方向相反，始终指向平衡位置的，称为移的方向相反，始终指向平衡位置的，称为线性回复力线性回复力。maf xmkmfa mk2 0222xdtxd 222dtxdxa简谐运动简谐运动微分方程微分方程65、简谐振动的运动学特征、简谐振动的运动学特征)t cos()t sin( ) cos(2 22 Adt

5、xdaAdtdxvtAx说明：说明：物体在简谐振动时，其位移、速度、加速度都是物体在简谐振动时，其位移、速度、加速度都是周期性周期性变变化的化的简谐振动不仅是周期性的，而且是有界的。简谐振动不仅是周期性的，而且是有界的。简谐运动微分方程的解为：简谐运动微分方程的解为：71、从受力角度来看、从受力角度来看动力学特征动力学特征kxf 2、从加速度角度来看、从加速度角度来看运动学特征运动学特征xa2 3、从位移角度来看、从位移角度来看运动学特征运动学特征) cos( tAx说明：说明：要证明一个物体是否作简谐振动，只要证明上面三个式子中的要证明一个物体是否作简谐振动，只要证明上面三个式子中的一个即可

6、，且由其中的一个可以推出另外两个；一个即可，且由其中的一个可以推出另外两个；要证明一个物体是否作简谐振动最简单的方法就是受力方析，要证明一个物体是否作简谐振动最简单的方法就是受力方析，得到物体所受的合外力满足回复力的关系。得到物体所受的合外力满足回复力的关系。8二、描述简谐振动的特征量二、描述简谐振动的特征量1、振幅、振幅A振动物体离开平衡振动物体离开平衡位置的最大位移的位置的最大位移的绝对值绝对值。振幅恒为正值，单位为米振幅恒为正值，单位为米(m);(m);振幅的大小与振动系统的能量有关，由系统振幅的大小与振动系统的能量有关，由系统的初始条件确定。的初始条件确定。x =Acos( t+ )9

7、2、周期、周期定义：物体作一次完全振动所需的时间，用定义：物体作一次完全振动所需的时间，用T表表示，单位为秒示，单位为秒(s) (cos) cos( TtAtAx 2T 2 T频率频率定义：单位时间内物体所作的完全振动的次数，定义：单位时间内物体所作的完全振动的次数，用用表示，单位为赫兹表示，单位为赫兹(Hz)。 21 T10角频率角频率定义：物体在定义：物体在2秒时间内所作的完全振动的次数，用秒时间内所作的完全振动的次数，用表表示，单位为弧度示，单位为弧度/秒秒(rad.s-1)。T 22 说明说明简谐运动的基本特性是它的周期性简谐运动的基本特性是它的周期性周期、频率或角频率均由振动系统本身

8、的性质所决定，故周期、频率或角频率均由振动系统本身的性质所决定，故称之为固有周期、固有频率或固有角频率。对于弹簧振子称之为固有周期、固有频率或固有角频率。对于弹簧振子kmTmkmk 2,21, 简谐运动的表达式可以表示为简谐运动的表达式可以表示为) 2cos() 2cos() cos( tAtTAtAx113、相位和初相位、相位和初相位相位相位 t 初相位初相位 对于一个简谐运动，若对于一个简谐运动，若振幅、周期和初相振幅、周期和初相位位已知，就可以写出完整的运动方程，即已知，就可以写出完整的运动方程，即掌握了该运动的全部信息，因此我们把振掌握了该运动的全部信息，因此我们把振幅、周期和初相位叫

9、做幅、周期和初相位叫做描述简谐振动的三描述简谐振动的三个特征量个特征量。124、常数、常数A和和 的确定的确定 sincos00AvAx )arctan(002020 xvvxA)t sin( ) cos( AdtdxvtAx说明：说明：(1) 一般来说一般来说 的取值在的取值在和和(或或0和和2)之间；之间；(2) 在应用上面的式子求在应用上面的式子求 时，时，一般来说有两个值，还要由初一般来说有两个值，还要由初始条件来判断应该取哪个值；始条件来判断应该取哪个值；(3)常用方法：由常用方法：由2020 vxA求求A，然后由，然后由x0=Acos v0=-Asin 两者的共同部分求两者的共同部

10、分求 。13三三 .简谐振动的描述简谐振动的描述1.解析法：解析法： x =Acos( t+ )角频率角频率 由由谐振系统确定。谐振系统确定。mk 对弹簧振子：对弹簧振子： 顺便指出，顺便指出，弹簧弹簧的串联和并联公式与的串联和并联公式与电阻电阻的串联和的串联和并联公式是并联公式是相反相反。 例如例如:一根倔强系数为一根倔强系数为k的轻弹簧的轻弹簧,减去一半后减去一半后,倔强系倔强系数是多少数是多少?11111kkkkk2114 振幅振幅A和初相和初相 由由初始条件初始条件(即即t=0时刻物体的运动时刻物体的运动状态状态)来确定：来确定：x =Acos( t+ ) = - Asin( t+ )

11、 o = - Asin 当当t=0时，时，xo =Acos sinAo)arctan(oox22020vxA15 例题例题7-1 一质点沿一质点沿x轴作谐振动，周期轴作谐振动，周期T= s, t=0时，时，,mxo2, s/mo22 求振动方程。求振动方程。解：解：22T4+ 43mtx)432cos(2得代入：代入：x =Acos( t+ ), 1tanoox222020vxA（m ）16 例题例题7-2 有一轻弹簧，当下端挂一个质量有一轻弹簧，当下端挂一个质量m1=80g的的物体而平衡时，伸长量为物体而平衡时，伸长量为4.9cm。用这个弹簧和质量。用这个弹簧和质量m2=40g的物体组成一弹

12、簧振子。若取平衡位置为原的物体组成一弹簧振子。若取平衡位置为原点，向上为点，向上为x轴的正方向。将轴的正方向。将m2从平衡位置向下拉从平衡位置向下拉2cm后，给予向上的初速度后，给予向上的初速度 o=10cm/s并开始计时，并开始计时，试求振动方程。试求振动方程。解：由解：由 m1g=k x , 得得16/1xgmk202mk t=0时时, xo=-2cm, o=10cm/smxo oxot=0=2.06cm22020vxA17ooxtan= 0.25 =14.04=0.24 radt=0时时, xo=-2cm, o=10cm/s应取：应取： =0.24 + =3.38 (rad)所求振动方程

13、为所求振动方程为 x =2.06cos(20t+3.38)cm把把 A=2.06cm, =20, =3.38 代入代入 x =Acos( t+ )mxo oxot=0182.矢量图解法矢量图解法旋转矢量法旋转矢量法oM =A负最大负最大 ( )平衡位置平衡位置(+ /2)平衡位置平衡位置(- /2) 矢量矢量oM绕绕o点以角速点以角速度度 作作逆时针逆时针的的匀速匀速转转动动, 端点端点M在在x轴上的投轴上的投影点影点(p点点)的位移：的位移： x =Acos( t+ ) 显然，显然，p点的运动就点的运动就是简谐振动。是简谐振动。 矢量矢量oM与与x轴正方向轴正方向间的夹角：间的夹角：( t+

14、 ) 相位相位正最大正最大 (0)x =Acos( t+ ) =- Asin( t+ )MAox oM转一圈转一圈,就是简谐就是简谐振动的一个周期振动的一个周期T 。px( t+ )19ox例题例题7-3 求简谐振动质点的初相求简谐振动质点的初相 。(1)t=0时，时，xo=-A, = 。 (2)t=0时，质点经过平衡时，质点经过平衡位置正向位置正向x轴正方向运动轴正方向运动, 则则 = 3 /2(或或- /2)。 (3)t=0时，时， xo=A/2，质点质点正向正向x轴负方向运动轴负方向运动, 则则 =xo =Acos (4)t=0时，时， 质质点正向点正向x轴正方向运动轴正方向运动, 则则

15、 =,Axo22 /3。A平衡位置平衡位置5 /45 /4（或（或3 /4 ）。）。 /320 例题例题7-4 一质量一质量m=9kg质点质点, 在力在力 (N)的作用下沿的作用下沿x轴运动。当轴运动。当t=0，xo=0; t=1s, =-2m/s, 求求振动方程。振动方程。xF42解解 质点受弹性回复力的作用，故作简谐振动。质点受弹性回复力的作用，故作简谐振动。由由,42xF,42k知知6 mkooxtan要想直接用下述公式求要想直接用下述公式求A、 是困难的：是困难的： 我们可利用旋转矢量先求出初相。我们可利用旋转矢量先求出初相。 ,T=12s。22020vxA21于是：于是：)26cos

16、(tAx)26sin(6tAdtdxt=1, 2)26sin(6A38A最后得：最后得：m)tcos(x26 38 由由t=0, xo=0， 知知 = /2；又因又因T=12s, t=1s, =-20, 振动振动x2超前超前x1( 2 - 1） ；0, 振动振动x2落后落后x1( 2 - 1) ；=0, 振动振动x2和和x1同相同相 ；= , 振动振动x2和和x1反相反相 。相差相差 = 2 - 1例：例： x =Acos( t+ ) =- Asin( t+ )= Acos( t+ + /2 )a =- 2Acos( t+ )= 2Acos( t+ + )=- 2x 超前超前x /2； a 超

17、前超前 /2； a与与 x反相反相。 28例：例： x1 =0.3cos( t ) x2 =0.4cos( t )23x2 超前超前 x123 =0.4cos( t )2x1 超前超前 x2229 例题例题7-7 一光滑斜面上的弹簧振子，已知一光滑斜面上的弹簧振子，已知m , k , 证证明它作谐振动，并求出周期。明它作谐振动，并求出周期。 解解 (1)找出平衡位置找出平衡位置:(2)将物体将物体m对平衡位置位移对平衡位置位移x；(3)沿斜面方向应用牛二定律：沿斜面方向应用牛二定律： mgsin -k(x+xo )=ma -kx = maxmka,mk kmT 22xa2比较：比较：是谐振动。

18、是谐振动。(T与倾角与倾角 无关无关)ox建立坐标；建立坐标；mgsin =kxo ，xokm mx30 例题例题7-8 一正方体形木块在水面上作谐振动，吃水一正方体形木块在水面上作谐振动，吃水深度为深度为h(水面下的木块高度水面下的木块高度)，求振动周期求振动周期T=？ 解解 设木块的质量为设木块的质量为m、边长为、边长为b, 则平衡条件为则平衡条件为 mg= 水gb2h建立图示坐标，建立图示坐标，由牛二定律有由牛二定律有令木块位移令木块位移x, 水gb2(h-x)-mg=ma即即 - 水gb2x =ma因因,12hmb水xhga,hg ghT 22比较：比较： a=- 2xoxhx31x

19、=Acos( t+ ) =- Asin( t+ )振动势能：振动势能：221kxEp振动动能：振动动能：221mEk 对弹簧振子对弹簧振子(任何一个简谐振动也都可以等效为一任何一个简谐振动也都可以等效为一个弹簧振子个弹簧振子)，有，有 k=m 2)(sin21222tAm)(cos2122tkA=恒量恒量221kAEEEpk总能：总能：32 1.由上面可以看出由上面可以看出,谐振系统的动能和势能都随时间谐振系统的动能和势能都随时间t作周期性的变化；而且作周期性的变化；而且, 动能和势能的周期为其振动动能和势能的周期为其振动周期的二分之一。周期的二分之一。势能最大时势能最大时,动能最小动能最小;

20、动能最大时动能最大时,势能最小势能最小。但系统的但系统的总机械能守恒总机械能守恒。)(sin21212222tAmmEk)(cos2121222tkAkxEpEkAdtETETpP21411202.平均势能：平均势能：平均动能：平均动能：EkAdtETETkk2141120221kAEEEpk=恒量恒量333.振动势能与弹性势能不一定相同。振动势能与弹性势能不一定相同。,212kxEp振动势能：振动势能：其中其中x是对平衡位置的位移。是对平衡位置的位移。,212kxEp弹性势能：弹性势能：其中其中x是弹簧的伸长量。是弹簧的伸长量。221kxEp振2)(21xxkEop弹例例221kxEEpp振

21、弹xo(原长原长)(平衡位置平衡位置)xmxomxo(原长原长)(平衡位置平衡位置)x34 例题例题7-9 如图，有一光滑水平面上的弹簧振子，弹如图，有一光滑水平面上的弹簧振子，弹簧的倔强系数簧的倔强系数k=24N/m, 物体的质量物体的质量m=6kg, 静止在平静止在平衡位置。设以一水平恒力衡位置。设以一水平恒力F=10N向左作用于物体，使向左作用于物体，使之由平衡位置向左运动了之由平衡位置向左运动了s=0.05m, 此时撤去外力此时撤去外力F。取物体运动到左方最远处开始计时，求：取物体运动到左方最远处开始计时，求：(1)物体的物体的振振动方程动方程; (2)何处何处Ek=Ep?解解 (1)

22、振动能量来源于外力的功：振动能量来源于外力的功：,212kASF A=0.204m,mk2 = x =0.204cos(2 t+ )m(2) 22221kxEEEkAEppkm.Ax144022smFkxo35例例7-10 一长度为一长度为l的无弹性细的无弹性细线，一端被固定在线，一端被固定在A点，另一点，另一端挂一质量为端挂一质量为m、体积很小的、体积很小的物体。静止时，细线沿竖直方物体。静止时，细线沿竖直方向，物体处于点向，物体处于点O，这是振动，这是振动系统的平衡位置。若将物体移系统的平衡位置。若将物体移离平衡位置，使细线与竖直方离平衡位置，使细线与竖直方向夹一小角度，然后将物体由向夹一

23、小角度，然后将物体由静止释放，物体就在平衡位置静止释放，物体就在平衡位置附近往返摆动起来，这种装置附近往返摆动起来，这种装置称为称为单摆单摆。证明单摆的振动是证明单摆的振动是简谐振动，并分析其能量。简谐振动，并分析其能量。36解：我们选择物体相对于平衡位置的角位移解：我们选择物体相对于平衡位置的角位移为描述为描述单摆位置的变量，并规定物体处于平衡位置右方，单摆位置的变量，并规定物体处于平衡位置右方，为正，处于平衡位置左方，为正，处于平衡位置左方， 为负。为负。物体受到两个力的作用，一个是重力物体受到两个力的作用，一个是重力mg，另一个是，另一个是细线的张力细线的张力T，将重力分解为径向分量，将

24、重力分解为径向分量mgcos 和切和切向分量向分量mgsin ，其中径向分量与张力，其中径向分量与张力T一起为物体一起为物体的运动提供向心力，切向分量作为物体的回复力的运动提供向心力，切向分量作为物体的回复力由于：由于：l = s，所以，所以2222dtdldtsdasin22mgdtdml单摆的振动方程为单摆的振动方程为(1)37当偏角当偏角很小时，很小时， sin ，式（，式（1）可写为）可写为mgdtdml22（2）即即022lgdtd0222dtd其中其中lg2（3）单摆的振动方程（单摆的振动方程（3）与弹簧）与弹簧振子的振动方程完全相似振子的振动方程完全相似)cos(0t单摆演示单摆

25、演示1单摆演示单摆演示238单摆系统的机械能包括两部分，一部分是物体的动能单摆系统的机械能包括两部分，一部分是物体的动能)(sin21)(21212220222tmldtdlmmvEk另一部分是系统的势能另一部分是系统的势能)cos1 (mglmghEp将将cos进行级数展开进行级数展开,!6!4!21cos642由于由于很小，我们只很小，我们只取前两项取前两项)(cos21212202tmglmglEp39可见，单摆系统的动能和势能都是时间的周期函数可见，单摆系统的动能和势能都是时间的周期函数单摆系统的总能量为：单摆系统的总能量为：2022202121mlmglEEEpk上式说明，尽管在单摆

26、系统的简谐振上式说明，尽管在单摆系统的简谐振动过程中，系统的动能和势能都随时动过程中，系统的动能和势能都随时间作周期性变化，但总能量式恒定不间作周期性变化，但总能量式恒定不变的，并与振幅的平方成正比。变的，并与振幅的平方成正比。40一、两个同方向同频率简谐振动的合成一、两个同方向同频率简谐振动的合成分振动：分振动：x1 =A1cos( t+ 1 ) x2 =A2cos( t+ 2 )合振动：合振动： x= x1+x2=A1cos( t+ 1 )+ A2cos( t+ 2 ) 利用三角公式或旋转矢量可求得合振动利用三角公式或旋转矢量可求得合振动: x= x1+x2= Acos( t+ )可见，可

27、见， (1) 合振动仍是同频率的谐振动。合振动仍是同频率的谐振动。 (2)合振动的振幅和初相合振动的振幅和初相, 用旋转矢量容易求得用旋转矢量容易求得:41 （1）由余弦定理，合振动的振幅为）由余弦定理，合振动的振幅为22112211coscossinsinarctanAAAA（2）合振动的初相：）合振动的初相：( ( 2-2- 1 1) )M1A1 1 1MA2xoxx1x2A A2 2 2M2x= x1+x2= Acos( t+ ) x1 =A1cos( t+ 1 ) x2 =A2cos( t+ 2 )(cos212212221AAAAA)cos(212212221AAAAA42 (3)合

28、振动的强弱，取决于两分振动的相位差：合振动的强弱，取决于两分振动的相位差： = 2 - 12k , k=0, 1, 2, , A=A1+A2 , 加强加强(2k+1) , k=0, 1, 2, , A=|A1-A2 |, 减弱减弱=其他情况，其他情况，A处于处于A1+A2 和和|A1-A2 |之间之间的某一确定值的某一确定值43 解解 合振动方程合振动方程：x =Acos( t+ ) 例题例题7-11 设设分振动：分振动： x1 =0.3cos( t+ )cm, x2 =0.4cos( t+ )cm，求合振动方程。求合振动方程。2=0.522112211coscossinsintanAAAA,

29、43 =180-36.86 =-0.64+ =2.5rad 合振动方程合振动方程：x =0.5cos( t+2.5 ) cmx0.30.4 A-36.86已知：已知：A1=0.3, A2=0.4, 1= /2, 2= )cos(212212221AAAAA44 例题例题7-12 t=0时，时， x1 和和 x2的的振动曲线如图所示，振动曲线如图所示，求合振动方程。求合振动方程。 解解 由图由图可知，可知，x1与与x2是反相的。因而是反相的。因而 合振幅合振幅: A= 0.12- 0.08=0.04; 合振动的初相合振动的初相: =- /2 (振幅大的分振动的初相振幅大的分振动的初相) 合振动的

30、角频率：合振动的角频率： =2 /T= x(m)t(s)x2x10.120.08o1 合振动方程合振动方程： x =0.04cos( t- /2 ) m45 例题例题7-13 两个同方向、同频率的谐振动合成后，合两个同方向、同频率的谐振动合成后，合振幅振幅A=20cm, 合振动与第一个振动的相差为合振动与第一个振动的相差为 /6, A1=17.3cm, 求：求：(1)A2=? (2)两两振动的相差振动的相差( 2 - 1)=? 解解 直接用下述公式是无法求解的：直接用下述公式是无法求解的：A1=17.3 1 1A=20 /6A2xo=10cm 此题宜用旋转矢量法求解。此题宜用旋转矢量法求解。由

31、图由图, 用余弦定理得：用余弦定理得：A2 2 2)cos(212212221AAAAA22112211coscossinsintanAAAA6cos212122AAAAA46用正弦定理有：用正弦定理有：6sin)(sin212AA 因因A=20, A2=10, 由上式由上式可可求出：求出：2)(12( ( 2-2- 1 1) )A1=17.3 1 1A=20 /6A2xoA2 2 247二、两个同方向频率相近的简谐振动的合成二、两个同方向频率相近的简谐振动的合成分振动：分振动：x1 =Acos( 1 t+ ) x2 =Acos( 2t+ )， 且且 1 与与 2相差很小。相差很小。 合振动：

32、合振动： x= x1+x2= )2cos(2cos22112ttA 由于由于 1 与与 2相差很小相差很小,故故 1 - 2比比 1 + 2小得多小得多; 即即t2cos12比比 的周期长得多的周期长得多！t2cos12 所以，合振动可近似看作是一个振幅缓慢变化的谐所以，合振动可近似看作是一个振幅缓慢变化的谐振动振动拍拍:),2cos(21tAxotAAo2cos21248显然，拍频显然，拍频 (振幅振幅Ao的变化频率的变化频率)为为 拍拍 = 2 - 1tAAo2cos212xt拍的应用：拍的应用：用音叉的振动来校准乐器；用音叉的振动来校准乐器；利用拍的规律测量超声波的频率；利用拍的规律测量

33、超声波的频率；在无线电技术中，可以用来测定无线电波在无线电技术中，可以用来测定无线电波频率以及调制频率以及调制49三、两个相互垂直的同频率简谐振动的合成三、两个相互垂直的同频率简谐振动的合成 x =Acos( t+ ) y =Bcos( t+ )从上两式中消去从上两式中消去t, 就得到合振动的轨迹方程为就得到合振动的轨迹方程为)(sin)cos(222222ABxyByAx 在一般情况下在一般情况下,这是一个椭圆方程。这是一个椭圆方程。 (1)当当 - =0时，上式为一直线：时，上式为一直线： xABy xy50 xAByxy（1）（）（2）合振动仍为谐振动）合振动仍为谐振动:22yxr (3

34、)当当 - = /2时，上式仍为一时，上式仍为一椭圆椭圆：12222ByAx合振动不再是谐振动。合振动不再是谐振动。)tcos(2221 AA(2)当当 - = 时，时， 上上式也为一直线：式也为一直线：若若A=B,椭圆变为圆椭圆变为圆51xy - = /2xy - =- /2（4）如果）如果 - 不为上述数值，那么合振动的轨不为上述数值，那么合振动的轨迹为边长分别为迹为边长分别为2A(x方向）和方向）和2B（y方向）的矩方向）的矩形范围内的任意确定的椭圆。形范围内的任意确定的椭圆。教材图教材图612画出了几种不同相位差所对应的合振动的画出了几种不同相位差所对应的合振动的轨迹图形。轨迹图形。5

35、2四、两个相互四、两个相互垂直不同频率的简谐运动的合成垂直不同频率的简谐运动的合成合成运动不是周期性的运动。下面就两种情况讨论合成运动不是周期性的运动。下面就两种情况讨论 视为同频率的合成：两个振动的相位差缓视为同频率的合成：两个振动的相位差缓慢地变化，质点运动的轨道循环变化。慢地变化，质点运动的轨道循环变化。012情况情况1：两个分振动的频率相差很小：两个分振动的频率相差很小合振动的轨道是周期性的有一定规则的合振动的轨道是周期性的有一定规则的稳定的闭合曲线。这种运动轨迹的图形稳定的闭合曲线。这种运动轨迹的图形称为称为利萨如图形利萨如图形。应用应用测量频率测量频率在示波器上，垂直方向与水平方向

36、同时输入两个振动，已在示波器上，垂直方向与水平方向同时输入两个振动，已知其中一个频率，则可根据所成图形与已知标准的利萨如知其中一个频率，则可根据所成图形与已知标准的利萨如图形去比较，就可得知另一个未知的频率。图形去比较，就可得知另一个未知的频率。2:1:yxTT情况情况2：两个分振动的频率相差较大，且有：两个分振动的频率相差较大，且有简单整数比关系简单整数比关系53一、一、阻尼振动阻尼振动dtdxvf振动系统受粘滞阻力与速度大小成正比，方向相反。振动系统受粘滞阻力与速度大小成正比，方向相反。弹性力或准弹性力和上述阻力作用下的动力学方程：弹性力或准弹性力和上述阻力作用下的动力学方程：1、阻尼振动

37、的概念、阻尼振动的概念振幅随时间的变化而减小的振动称为阻尼振动。振幅随时间的变化而减小的振动称为阻尼振动。2、阻尼振动的运动方程、阻尼振动的运动方程kxdtdxdtxdm22022022xdtdxdtxdm2mk 20 固有角固有角频率频率阻尼阻尼常数常数演示演示54情况情况1：欠阻尼欠阻尼202220 )cos()(0teAtxt这种情况称为这种情况称为欠阻尼欠阻尼阻力使周期增大阻力使周期增大3、讨论、讨论t欠阻尼欠阻尼)(tx由初始条件决定由初始条件决定A0和初相位和初相位 ,设设00)0(,)0(,0vvxxt即有即有： cossincos00000AAvAx2200200)(xvxA0

38、00tanxxv55tteCeCtx)(2)(1202202 )(t过阻尼过阻尼)(tx无振动发生无振动发生202情况情况2：过阻尼过阻尼t临界阻尼临界阻尼)(txtetCCtx 21)()(情况情况3：临界阻尼临界阻尼202220是从有周期性因子是从有周期性因子 到无周期性的到无周期性的临界点临界点。称之为临界阻尼情况。称之为临界阻尼情况。应用在天平调衡中。应用在天平调衡中。56系统受力：弹性力系统受力：弹性力 -kx；阻尼力阻尼力tddx 周期性驱动力周期性驱动力 f =Fcos ttFtddxkxtdxdmcos22二、受迫振动二、受迫振动 在周期性外力作用下发生的振动，称为在周期性外力

39、作用下发生的振动，称为受迫振动受迫振动。该外力称为驱动力。该外力称为驱动力。振动方程可写为：振动方程可写为：tmFxtddxtdxdcos22022令令,mkom257该微分方程的解为该微分方程的解为tmFxtddxtdxdcos22022)cos()cos(22tAtAexot 可以看出可以看出,此等幅振动的频率此等幅振动的频率 就是驱动力的频率就是驱动力的频率,其振幅和初相为其振幅和初相为 上式表明上式表明,受迫振动可以看成是两个振动合成的。第受迫振动可以看成是两个振动合成的。第一项表示的是减幅振动。经过一段时间后一项表示的是减幅振动。经过一段时间后,这一分振动这一分振动就减弱到可以忽略不

40、计了。而第二项表示的是受迫振就减弱到可以忽略不计了。而第二项表示的是受迫振动达到稳定状态时的等幅振动。因此动达到稳定状态时的等幅振动。因此,稳态解为稳态解为 x =Acos( t- ) 58 可以看出，可以看出， A、 不仅不仅与振动系统自身的性质有关，与振动系统自身的性质有关，而且与驱动力的频率和幅度有关。而且与驱动力的频率和幅度有关。 222tano222224)(/omFA59222or三、共振三、共振 受迫振动的振幅与驱动力的频率有关受迫振动的振幅与驱动力的频率有关,当驱动力当驱动力频率达某一值时频率达某一值时,振幅达最大值。用求极值的方法可振幅达最大值。用求极值的方法可以求出使振幅达

41、到极大值的角频率为以求出使振幅达到极大值的角频率为相应的最大振幅为相应的最大振幅为222/ormFA 在弱阻尼在弱阻尼(即即 o)的情况下的情况下,由式可以看出由式可以看出,当当 r= o , 即驱动力频率等于振动系统的固有频率时即驱动力频率等于振动系统的固有频率时,振幅达到最大值。我们把这种振幅达到最大值的现振幅达到最大值。我们把这种振幅达到最大值的现象叫做象叫做共振共振。荡秋千演示荡秋千演示60应用应用防止防止钢琴、小提琴等乐器利用共振来提高音响效果；钢琴、小提琴等乐器利用共振来提高音响效果；收音机利用电磁共振进行选台；收音机利用电磁共振进行选台；核内的核磁共振被用来进行物质结构的研究和核

42、内的核磁共振被用来进行物质结构的研究和医疗诊断等。医疗诊断等。改变系统的固有频率或外力的频率；改变系统的固有频率或外力的频率；破坏外力的周期性；破坏外力的周期性；增大系统的阻尼；增大系统的阻尼；对精密仪器使用减振台。对精密仪器使用减振台。6162 在弹性介质中，各质点之间是以弹性力相互联系在弹性介质中，各质点之间是以弹性力相互联系着的。着的。一、机械波的产生和传播一、机械波的产生和传播7-4 波动的基本概念波动的基本概念 产生机械波的条件：产生机械波的条件： 波源波源产生机械振动；产生机械振动； 弹性介质弹性介质传播振动状态。传播振动状态。 当介质中的一个质点开始振动后当介质中的一个质点开始振

43、动后,在弹性力的在弹性力的作用下作用下,就会带动邻近质点振动就会带动邻近质点振动,邻近质点又带动更远邻近质点又带动更远质点振动。这样依次带动质点振动。这样依次带动,就把振动由近及远地传播就把振动由近及远地传播出去出去,形成了波动。形成了波动。u63t = 00481620 12 t = T/4 t = T/2 t = 3T/4t = T 64容易看出容易看出, , 沿着波的传播方向沿着波的传播方向, , 振动是依次落后的。振动是依次落后的。P点比点比o点时间落后：点时间落后：uxt P点比点比o点位相落后：点位相落后：uxt)2:(T注意(这里：这里：u是波速是波速)pyuxo(波源波源)x值

44、得注意的是：值得注意的是：波动是波源的振动状态或波动能量在介质中的传播波动是波源的振动状态或波动能量在介质中的传播介质中的质点并不随波前进，只是在各自的平衡位置附介质中的质点并不随波前进，只是在各自的平衡位置附近往复运动。近往复运动。65二、横波与纵波二、横波与纵波波的传播方向波的传播方向向右向右波的传播方向波的传播方向向右向右质点振动方向质点振动方向水平水平uabxyo质点质点 振动方向振动方向向上向上a分类标准分类标准介质质点的振动方向与介质质点的振动方向与波动的传播方向的关系波动的传播方向的关系1、横波横波质点的振动方向与波的质点的振动方向与波的传播方向垂直。传播方向垂直。波峰波峰波形凸

45、起部分波形凸起部分波谷波谷波形凹下部分波形凹下部分2、纵波纵波质点的振动方向与波的质点的振动方向与波的传播方向平行。传播方向平行。纵波的传播表现为纵波的传播表现为疏密疏密状态沿波传播方向移动。状态沿波传播方向移动。66三、波面和波线三、波面和波线波线波线(波射线波射线) 波的传播方向。波的传播方向。 波面波面(波阵面波阵面) 波动过程中，振动相位相同的点连波动过程中，振动相位相同的点连成的面。最前面的那个波面称为波前。成的面。最前面的那个波面称为波前。 平面波平面波波面为平面的波动。本章只讨论这种波。波面为平面的波动。本章只讨论这种波。 球面波球面波波面为球面的波动。波面为球面的波动。 在各向

46、同性媒质中，波线总是与波面垂直。在各向同性媒质中，波线总是与波面垂直。 波面波面 波面和波线波面和波线都是为了形象地描述波在空间的传播而引都是为了形象地描述波在空间的传播而引入的概念。入的概念。67四、波速四、波速 波长波长 波的周期和频率波的周期和频率 1、 波速波速u单位时间内振动传播的距离，也就是单位时间内振动传播的距离，也就是波面向前推进的速率。波速完全由媒质的性质波面向前推进的速率。波速完全由媒质的性质(弹性弹性和惯性和惯性)来确定。来确定。如液体、气体中的纵波，波速：如液体、气体中的纵波，波速： Bu 体变弹性模量体变弹性模量质量密度质量密度(惯性惯性)固体中的横波，波速：固体中的

47、横波，波速： Gu 切变弹性模量切变弹性模量纵波，波速：纵波，波速： Yu 杨氏弹性模量杨氏弹性模量柔绳中的横波，波速：柔绳中的横波，波速： Tu 绳中的张力绳中的张力质量线密度质量线密度682、波长、波长反映波动的空间周期性反映波动的空间周期性定义：定义：同一波线上两个相邻的、相位同一波线上两个相邻的、相位差为差为2 的振动质点之间的距的振动质点之间的距离，离，或或沿波的传播方向，相邻沿波的传播方向，相邻的两个同相质点之间的距离叫的两个同相质点之间的距离叫波长波长。说明：说明：波长可形象地想象为一个完整的波长可形象地想象为一个完整的“波波”的长度；的长度；横波横波：相邻两个波峰或波谷之间的距

48、离相邻两个波峰或波谷之间的距离纵波纵波：相邻两个密部中心或疏部中心之间的距离相邻两个密部中心或疏部中心之间的距离xyo693、周期和频率、周期和频率反映波动的时间周期性反映波动的时间周期性定义：定义：周期周期：一个完整的波（即一个波长的波）通过：一个完整的波（即一个波长的波）通过波线上某点所需要的时间，叫周期，用波线上某点所需要的时间，叫周期，用T T表示。表示。频率频率：周期的倒数叫做频率，用：周期的倒数叫做频率，用v v表示表示T/1 说明：说明：由于波源作一次完全的振动，波就前进一个波长的距离，由于波源作一次完全的振动，波就前进一个波长的距离，因此因此波的周期等于波源振动的周期；波的周期

49、等于波源振动的周期；波的周期只与振源有关，而与传播介质无关。波的周期只与振源有关，而与传播介质无关。70 周期周期T反映波的时间周期性，而波长反映波的时间周期性，而波长 反映的是波的反映的是波的空间周期性。显然，周期空间周期性。显然，周期T也就是波传播一个波长距也就是波传播一个波长距离所需的时间。离所需的时间。Tu 71例例7-15：在室温下，已知空气中的声速为：在室温下，已知空气中的声速为u1=340ms-1，水中的声水中的声速为速为u2=1450ms-1，求频率为求频率为200Hz的声波在空气和水中的波长。的声波在空气和水中的波长。解：由解：由 u 得得 空气中空气中 mu7 . 1200

50、34011 水中水中 mu25. 7200145022 结论结论：同一频率的声波，在水中的波长要比在空气中的波长要长。：同一频率的声波，在水中的波长要比在空气中的波长要长。原因原因：波速决定于介质，频率决定与振源，所以同一波源发出的：波速决定于介质，频率决定与振源，所以同一波源发出的一定频率的波在不同介质中传播时，频率不变，但波速不同，因一定频率的波在不同介质中传播时，频率不变，但波速不同，因而波长也不同。而波长也不同。721.波的叠加原理波的叠加原理五、五、 波动所遵从的基本原理波动所遵从的基本原理 大量的观察和研究表明大量的观察和研究表明:几列波可以保持各自的几列波可以保持各自的特点特点(

51、频率、波长、振幅、振动方向等频率、波长、振幅、振动方向等)同时通过同一同时通过同一媒质媒质,好像在各自的传播过程中没有遇到其他波一样。好像在各自的传播过程中没有遇到其他波一样。因此因此,在几列波相遇或叠加的区域内在几列波相遇或叠加的区域内,任一点的振动任一点的振动,为为各个波单独在该点产生的振动的合成。这一规律称为各个波单独在该点产生的振动的合成。这一规律称为波的独立传播原理波的独立传播原理或或波的叠加原理波的叠加原理。 管弦乐队合奏或几个人同时讲话时管弦乐队合奏或几个人同时讲话时,在空气中同时在空气中同时传播着许多声波传播着许多声波,但我们仍能够辩别出各种乐器的音调但我们仍能够辩别出各种乐器

52、的音调或某个人的声音或某个人的声音,这就是波的叠加原理的具体例子。这就是波的叠加原理的具体例子。 数学方法：傅里叶分析。数学方法：傅里叶分析。732. 惠更斯原理惠更斯原理 介质中波动传播到的各点介质中波动传播到的各点,都可以看作是发射子波都可以看作是发射子波的波源的波源,其后任一时刻其后任一时刻,这些子波的包络就是新的波面。这些子波的包络就是新的波面。这就是惠更斯原理。这就是惠更斯原理。 作用：知道某一时刻的波阵面作用：知道某一时刻的波阵面,用几何作图的方法用几何作图的方法就能确定下一时刻的波阵面就能确定下一时刻的波阵面,从而确定波的传播方向。从而确定波的传播方向。球球面面波波 tt + t

53、平面波平面波t+ t时刻波面时刻波面u t波传播方向波传播方向t 时刻波面时刻波面74惠更斯原理的不足：不能求出波的强度分布。惠更斯原理的不足：不能求出波的强度分布。a 用惠更斯原理可以解释波的衍射现象。所谓用惠更斯原理可以解释波的衍射现象。所谓波的波的衍射衍射是指波在传播过程中遇到障碍物时是指波在传播过程中遇到障碍物时,其传播方向其传播方向发生改变发生改变,能绕过障碍物的边缘继续前进且强度重新能绕过障碍物的边缘继续前进且强度重新分布的现象分布的现象。 我们用惠更斯原理画出了我们用惠更斯原理画出了新的波阵面及波的传播方向。很明显新的波阵面及波的传播方向。很明显,波已绕过障碍波已绕过障碍物的边缘

54、而传播了物的边缘而传播了,即发生了衍射现象。若缝的宽度即发生了衍射现象。若缝的宽度比波长小得多时比波长小得多时,衍射现象将更加显著。衍射现象将更加显著。在下图中在下图中,75例例7-16 在波线上有相距在波线上有相距2.5 cm的的A、B两点，已知两点，已知点点B的振动相位比点的振动相位比点A落后落后300,振动周期为振动周期为2.0s，求，求波速和波长。波速和波长。解：我们知道：波线上相距解：我们知道：波线上相距的两点的相位差为的两点的相位差为2，而现在已知而现在已知波线上相距波线上相距2.5 cm的的A、B两点两点的相的相位差位差300 /6，因此有：因此有：6105 . 222得：m30

55、. 0smTu/15. 0230. 076一、平面简谐波的概念一、平面简谐波的概念波源作简谐振动，波动所到之处的各个质点也在作简谐振波源作简谐振动，波动所到之处的各个质点也在作简谐振动，相应的波称为动，相应的波称为简谐波简谐波。任意一种复杂的波都可以表示。任意一种复杂的波都可以表示为若干不同频率、不同振幅的简谐波的合成。波面为平面为若干不同频率、不同振幅的简谐波的合成。波面为平面的简谐波称为的简谐波称为平面简谐波平面简谐波。二、平面简谐波的波函数二、平面简谐波的波函数uxtAy cos0波源波源X轴上任一点轴上任一点P(x)，时间上要落，时间上要落后后=x/u/u，P处振动的相位要比处振动的相

56、位要比O处的相位落后处的相位落后 uxtAtAyP coscos演示演示7-5 平面简谐波的平面简谐波的波函数波函数77平面简谐波的波函数平面简谐波的波函数 uxtAy cos xTtAy2cos xtAy2cos若考虑若考虑O处质点的振动初相位处质点的振动初相位 uxtAycos kxtAy cos /2 k波数波数波数为波数为2米内所米内所包含的完整波的包含的完整波的数目。数目。78三、波动中质点振动的速度和加速度三、波动中质点振动的速度和加速度 uxtAtyauxtAtyv cos sin 222四、沿四、沿X轴负方向传播的平面简谐波的表达式轴负方向传播的平面简谐波的表达式 xtAyxT

57、tAykxtAyuxtAy2cos2cos) cos(cos演示演示79五、波函数的物理意义五、波函数的物理意义1、x一定，则位移仅是时间一定，则位移仅是时间的函数，对于的函数，对于x=x1 12cosxtAy质点的振动方程质点的振动方程2、t 一定，则位移仅是坐标的函一定，则位移仅是坐标的函数，对于数，对于 t=t1 xtAy2cos1对于不同的点对于不同的点 22112 2 xtxt )(2)2 ()2 (12212112xxxtxt 21122x 演示演示803、x 和和 t 都变化都变化波函数表示波线上所有质点在不同时刻的位移。波函数表示波线上所有质点在不同时刻的位移。(x,t)与（与

58、（x+ x,t+ t)处的相位相同处的相位相同 )()(22xxttuxut tux 结论：波的传播是相结论：波的传播是相位的传播（行波）位的传播（行波）演示演示81 例题例题7-17 已知波动方程：已知波动方程： ),)(212(cos5 . 0SIxty 求：求：(1)此波的传播方向，波的振幅、周期、频率、此波的传播方向，波的振幅、周期、频率、波长和波速，以及坐标原点的振动初相；波长和波速，以及坐标原点的振动初相； (2)x=2m处质点的振动方程，及处质点的振动方程，及t=1s时该质点的速时该质点的速度和加速度。度和加速度。 (3)x1=1m和和x2=2m两点的相差。两点的相差。 解解 (

59、1)比较法比较法。2)42(2cos5 . 0 xtyTtAy(2cos)ox 波沿波沿x轴正方向传播；轴正方向传播；A=0.5m, T=2s, =1/2Hz, =4m, u= /T=2m/s, 原点的振动初相原点的振动初相 o= /2。82 (2)将将x=2m代入波动方程就得该代入波动方程就得该处质点的振动方程：处质点的振动方程：)(212(cos5 . 0SIxtymty)2cos(5 . 0t=1s时该质点的速度和加速度为时该质点的速度和加速度为)2sin(5 . 0tdtdy)2cos(5 . 02tdtdat=1-0.5(m/s)t=10(3)x1=1m和和x2=2m两点的相差：两点

60、的相差：)(212xx 2) 12(4283 例题例题7-18 一波动以一波动以u=20cm/s沿沿x轴负方向传播，轴负方向传播，A点的振动方程为点的振动方程为 yA=0.4cos4 t(cm), 求求波动方程：波动方程： (1)以以A为坐标原点；为坐标原点； (2)以以B为坐标原点。为坐标原点。 解解 (1)以以A为坐标原点。为坐标原点。 tAy(cos)oux=0.4cos4(t20 x)cmx5cmABux5cmABuyo1.标准函数法：标准函数法：84已知已知A点的振动方程为点的振动方程为 yA=0.4cos4 t(cm)P(x)点比点比已知点已知点A时间时间超前：超前：uxt x5c