微分方程初值问题求解matlab实验

1、数学建模与数学实验课程实验报告 实验名称 微分方程初值问题求解matlab实验 班级学号姓名序号任课教师实验地点数学实验中心评分一、实验目的1、 学习简单问题的常微分方程建模。2、 学习并理解食饵-捕食者模型；3、 掌握微分方程（组）初值问题的matlab数值求解；二、实验要求和结果1.地中海鲨鱼问题意大利生物学家Ancona曾致力于鱼类种群相互制约关系的研究，他从第一次世界大战期间,地中海各港口捕获的几种鱼类捕获量百分比的资料中，发现鲨鱼等的比例有明显增加（见下表），而供其捕食的食用鱼的百分比却明显下降.显然战争使捕鱼量下降，食用鱼增加，鲨鱼等也随之增加，但为何鲨鱼的比例大幅增加呢？ 年代1

2、9141915191619171918百分比11.921.422.121.236.4年代19191920192119221923百分比27.316.015.914.819.71符号说明：食饵在t时刻的数量； 捕食者在t时刻的数量；食饵独立生存时的增长率；捕食者独自存在时的死亡率；捕食者掠取食饵的能力； 食饵对捕食者的供养能力.e捕获能力系数2基本假设：（1）食饵由于捕食者的存在使增长率降低，假设降低的程度与捕食者数量成正比； （2）捕食者由于食饵为它提供食物的作用使其死亡率降低或使之增长，假定增长 的程度与食饵数量成正比。3模型建立与求解 模型（一） 不考虑人工捕获 针对一组具体的数据用Mat

3、lab软件进行数值求解，画出食饵和捕食者图形以及相轨线图.设食饵和捕食者的初始数量分别为，对于数据，的终值经试验后确定为15，即模型为： 解：Matlab运行 首先建立M文件fun.m如下：function dx=fun(t,x)dx=zeros(2,1)dx(1)=x(1)*(1-0.1*x(2);dx(2)=x(2)*(-0.5+0.02*x(1); 然后，输入以下命令： t,x=ode45(fun,0 15,25 2); plot(t,x(:,1),-,t,x(:,2),*) plot(x(:,1),x(:,2)x1(t)和x2(t)的曲线图如下x2(t)x1(t)食饵捕食者图形 相轨线

4、y(x)的图形如下：数值结果为t=77*1double, x=77*2double.该模型反映了在没有人工捕获的自然环境中食饵与捕食者之间的制约关系，没有考虑食饵和捕食者自身的阻滞作用，是最简单的模型。食饵的量增加，捕食者也随之增加；食饵的量减少，捕食者的量也随之减少。可以猜想x1(t)和x2(t)都是周期函数。而且它们的循环是有一定周期的。模型（二） 考虑人工捕获设表示捕获能力的系数为e，相当于食饵的自然增长率由r1 降为r1-e，捕食者的死亡率由r2 增为 r2+e设战前捕获能力系数e=0.3, 战争中降为e=0.1, 则战前与战争中的模型分别为: 建立主程序shark1.m, 求解两个方

5、程，并画出两种情况下鲨鱼数在鱼类总数中所占比例 x2(t)/x1(t)+x2(t)解：先在matlab中建立M文件shier1.m:function dx=shier1(t,x)dx=zeros(2,1);dx(1)=x(1)*(0.7-0.1*x(2);dx(2)=x(2)*(-0.8+0.02*x(1);再在matlab中先建立M文件shier2.m：function dx=shier2(t,x)dx=zeros(2,1);dx(1)=x(1)*(0.9-0.1*x(2);dx(2)=x(2)*(-0.6+0.02*x(1);然后在matlab中输入以下命令：t,x=ode45(shier

6、1,0 15,25 2);plot(t,x(:,2)./(x(:,1)+x(:,2),-)t,x=ode45(shier2,0 15,25 2);plot(t,x(:,2)./(x(:,1)+x(:,2),*)求解结果：战前x=65*2double t=65*1double 战争中x=77*2double t=77*1double战前战争中结论：战争中鲨鱼的比例比战前高。 2.慢跑者与狗 一慢跑者在平面上沿着他喜欢的路径跑步，突然遭到一只狗的攻击，这只狗以恒定的速度跑向慢跑者，试计算狗追赶的轨迹。并就当慢跑者沿路径或（t为时间参数）跑动时，给出具体的数值结果和运动轨迹图（狗的初始位置和速度可以

7、自行设定）。解：1. 模型建立 当慢跑者沿路径2慢跑时，设时刻t慢跑者的坐标为（X(t),Y(t),狗的坐标为（x(t),y(t),狗的速率为w=20,则X=10+20cos t, Y=20+15sin t, 狗从（0,0）出发，建立狗的运动轨迹的参数方程： x(0)=0,y(0)=02. 模型求解建立M文件eq2.m如下：function dy=eq2(t,y)dy=zeros(2,1);dy(1)=20*(10+20*cos(t)-y(1)/sqrt(10+20*cos(t)-y(1)2+(20+15*sin(t)-y(2)2);dy(2)=20*(20+15*sin(t)-y(2)/sq

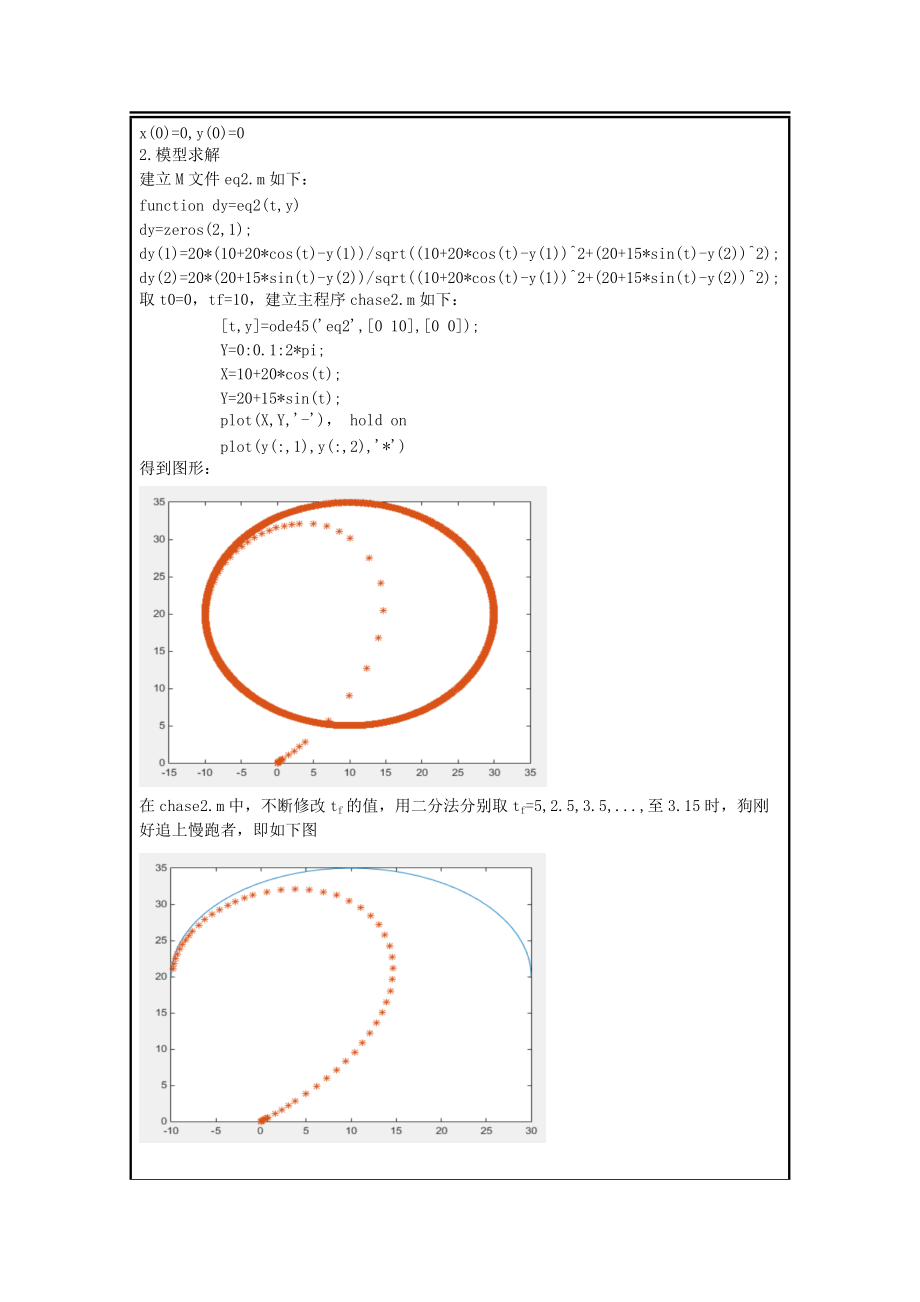
8、rt(10+20*cos(t)-y(1)2+(20+15*sin(t)-y(2)2);取t0=0，tf=10，建立主程序chase2.m如下： t,y=ode45(eq2,0 10,0 0); Y=0:0.1:2*pi; X=10+20*cos(t); Y=20+15*sin(t); plot(X,Y,-)， hold on plot(y(:,1),y(:,2),*)得到图形：在chase2.m中，不断修改tf的值，用二分法分别取tf=5,2.5,3.5,.,至3.15时，狗刚好追上慢跑者，即如下图三、思考 自然界中不少吃农作物的害虫都有其天敌益虫，也就是以害虫为食饵的捕食者。因此害虫和益虫也构成了一个食饵捕食者系统。如果人类使用的某种杀虫剂，既能杀死害虫，也能杀