中考数学压轴题之二次函数(中考题型整理,突破提升)附详细答案

1、一、二次函数真题与模拟题分类汇编(难题易错题)1.在平面直角坐标系中，点O为坐标原点，抛物线y=ax2+bx+c与x轴交于点A ( - 1, 0) , B (3, 0),与y轴交于点C (0. 3),顶点为G.(1)求抛物线和直线AC的解析式；(2)如图，设E (m, 0)为x轴上一动点，若4CGE和ACGO的面积满足Sacge =4CGOt求点E的坐标：y= - x2+2x+3：直线 AC 解析式为：y=3x+3： (2)点 E (3)存在以P. M, N为顶点的三角形为等腰直角三角(3)如图，设点P从点A出发，以每秒1个单位长度的速度沿x轴向右运动，运动时间 为ts,点M为射线AC上一动点

2、，过点M作MNII x轴交抛物线对称轴右侧部分于点 N.试探究点P在运动过程中，是否存在以P, M, N为顶点的三角形为等腰直角三角形? 若存在，求出t的值：若不存在，请说明理由.【答案】(1)抛物线解析式为: 坐标为(1, 0)或(-7, 0)；100 13 13形，t Tjtfi 为“ 49 .或或 N" ,【解析】【分析】(1)用待定系数法即能求出抛物线和直线AC解析式.(2) 4CGE与ACGO虽然有公共底边CG,但高不好求，故把 CGE构造在比较好求的三 角形内计算.延长GC交x轴于点F,则4FGE与4FCE的差即为4CGE.(3)设M的坐标(e, 3e+3),分别以M、N

3、、P为直角顶点作分类讨论，利用等腰直角 三角形的特殊线段长度关系，用e表示相关线段并列方程求解，再根据e与AP的关系求t 的值.【详解】(1) ; 抛物线 y=”2+bx+c 过点 A (-1, 0) , B (3, 0) , C (0, 3),a= - 1b=2c=3a-b + c=09a + 3b + c = 0 解但.0 + 0 + c = 3 '解也 ，抛物线解析式为：y=-x2+2x+3. 设直线AC解析式为y=kx+3, k+3=0,得：k=3，直线AC解析式为：y=3x+3.（2）延长GC交x轴于点F,过G作GHLx轴于点H,y=-x2+2x+3=- (x-1) 2+4,

4、/. G (1, 4) , GH=4,113Sa cgo=OC>Xg-x3x1,44 3S« cgeSa cgo、x,=2,若点E在x轴正半轴上，设直线 CG： y=kix+3,ki+3=4 得：ki=l,.,直线CG解析式:y=x+3,F (3, 0),E (m, 0),EF=m- (-3) =m+3,1111ni + 3.Fcge二Safge-Safce下EF.GHEFPCqEF. (GH-OC) = ( m+3) (4-3),m + 3二一=2,解得：m=l,E的坐标为(1, 0).若点E在x轴负半轴上，则点E到直线CG的距离与点(1, 0)到直线CG距离相等， 即点E到

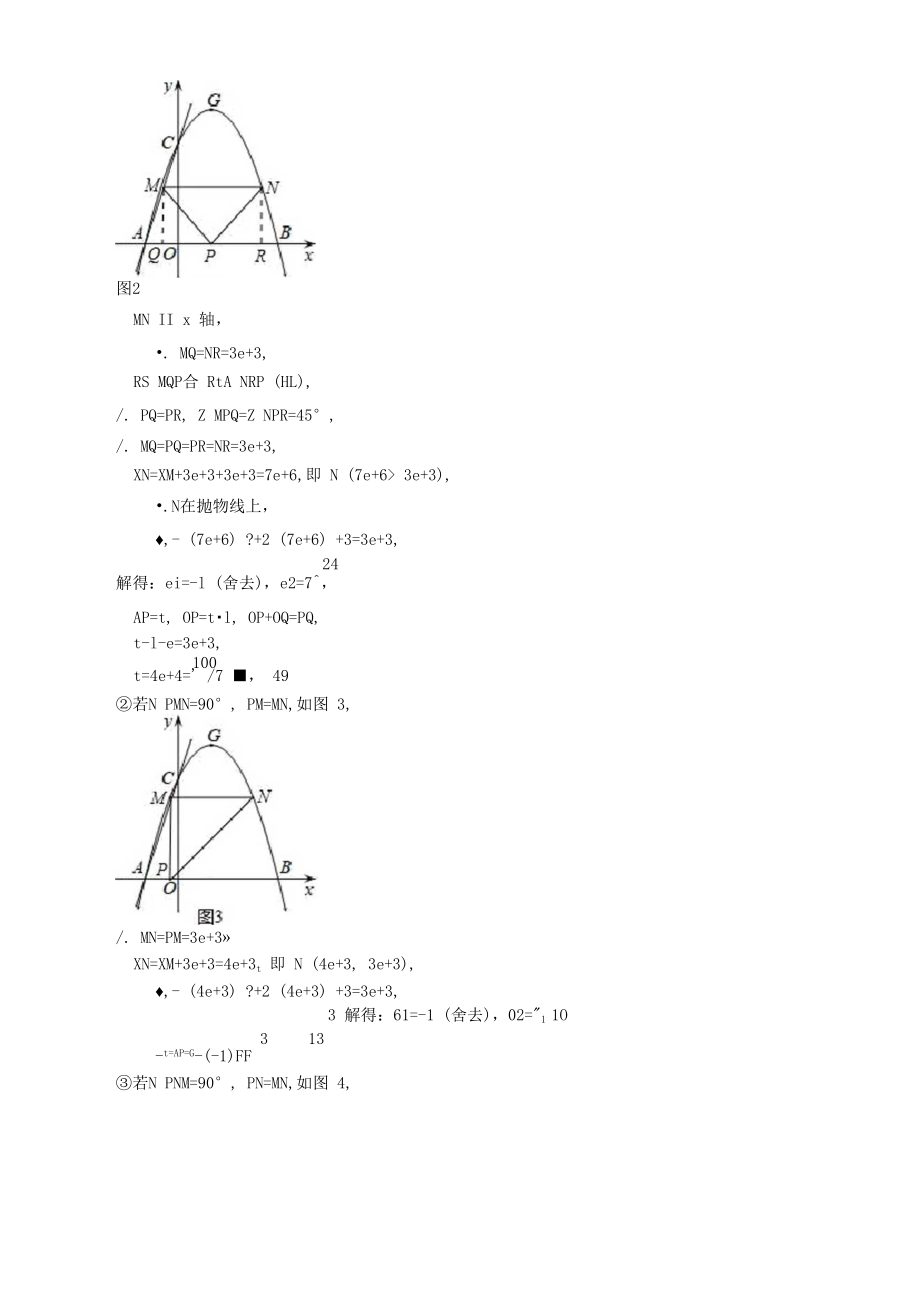
5、F的距离等于点(1, 0)到F的距离，/. EF=-3-m=l- (-3) =4,解得：m=-7 即 E (-7, 0),综上所述，点E坐标为(1, 0)或(-7, 0).(3)存在以P. M. N为顶点的三角形为等腰直角三角形，设 M (e» 3e+3),则 yN=yM=3e+3,若NMPN二90。，PM=PN,如图2,过点M作MCLLx轴于点Q,过点N作NRJLx轴于点R,图2MN II x 轴， . MQ=NR=3e+3,RS MQP合 RtA NRP (HL),/. PQ=PR, Z MPQ=Z NPR=45°,/. MQ=PQ=PR=NR=3e+3,XN=XM+3

6、e+3+3e+3=7e+6,即 N (7e+6> 3e+3), .N在抛物线上， ,- (7e+6) ?+2 (7e+6) +3=3e+3,24解得：ei=-l (舍去)，e2=7，AP=t, OP=tl, OP+OQ=PQ,t-l-e=3e+3,100t=4e+4=' /7 ， 49若N PMN=90°, PM=MN,如图 3,/. MN=PM=3e+3»XN=XM+3e+3=4e+3t 即 N (4e+3, 3e+3), ,- (4e+3) ?+2 (4e+3) +3=3e+3,3 解得：61=-1 (舍去)，02="1 1O313 -t=AP=

7、G-(-1)FF若N PNM=90°, PN=MN,如图 4,13t=AP=OA+OP=l+4e+3=-rt4100 13 13综上所述，存在以P，M, N为顶点的三角形为等腰直角三角形，t的值为由域正或彳.【点睛】本题考查了待定系数法求函数解析式，坐标系中三角形面积计算，等腰直角三角形的性 质，解一元二次方程，考查了分类讨论和方程思想.第（3）题根据等腰直角三角形的性质 找到相关线段长的关系是解题关键，灵活运用因式分解法解一元二次方程能简便运算.2. （2017南宁，第26题，10分）如图，已知抛物线疯3 9。与坐标轴交于4 8, C三点，其中C（0, 3） , N84：的平分线A

8、E交y轴于点。，交8c于点&过点。 的直线/与射线4C，八8分别交于点M, N.（1）直接写出a的值、点八的坐标及抛物线的对称轴；（2）点P为抛物线的对称轴上一动点，若4 %。为等腰三角形，求出点P的坐标：（3）证明：当直线/绕点。旋转时，+ 均为定值，并求出该定值.AM AN【答案】（1）a=-；, A（ -0）,抛物线的对称轴为x=JJ： （2）点P的坐标为（技 0）或（/, -4） ； （3）三.【解析】试题分析：（1）由点C的坐标为（0, 3）,可知-9a=3,故此可求得a的值，然后令y=0得到关于x的方程，解关于x的方程可得到点A和点8的坐标，最后利用抛物线的对称性可确定出抛

9、物线的对称轴：（2）利用特殊锐角三角函数值可求得N 640=60。，依据4E为N84C的角平分线可求得Z DAO=30°,然后利用特殊锐角三角函数值可求得OD=1,则可得到点。的坐标.设点P的 坐标为（JJ，。）.依据两点的距离公式可求得4D、AP. 0P的长，然后分为AD=%、 AD=DP. 4%DP三种情况列方程求解即可：（3）设直线MN的解析式为片kx+1,接下来求得点M和点N的横坐标，于是可得到AN 的长，然后利用特殊锐角三角函数值可求得4M的长，最后将AM和4N的长代入化简即 可.试题解析：（1）VC （0, 3）,.-90=3,解得：。二一1.3令 y=0 得：4%2-2

10、戊工一9=0' .。工0, 小一2 后一9 = 0,解得：、=-寿或x=3/，点八的坐标为（-万，0）, 8（3括，0），抛物线的对称轴为秒垂. 。=6 OC=3, tanZ CAO=y/J 9N 640=60。.4E为N8AC的平分线，/。40=30°,二.DO=五40=1,.,点。的坐标为（0, 1）.3设点P的坐标为（JJ,。）.依据两点间的距离公式可知：4）2=4,4a=12+/,。尸=3+ （O-l） 2.当4）=%时，4=12+4,方程无解.当4）=DP时，4=3+ （a-1） 2,解得。=0或方2 （舍去），点P的坐标为（JJ, 0）.当 4>=DP 时，

11、12+4=3+ （a- 1） 2,解得 a=-4, .点 P 的坐标为（, -4）.综上所述，点P的坐标为（/, 0）或（/，-4）.（3）设直线的解析式为y=mx+3,将点A的坐标代入得：-/ + 3 = 0,解得: m=G，.直线AC的解析式为），=后+ 3.设直线MN的解析式为y=kx+l.把片0代入片kx+1得：kx+l=0,解得:点N的坐标为（一!，0）,K将y = JWl + 3与片kx+1联立解得:过点M作MGLc轴，垂足为G.则4G=2X 尸9k-巾2k-小2点M的横坐标为一上73Z M4G=60°,4N4GM=90°, /. AM=2AG=t= +k6I

12、、 1 _ kf k3k-追 正电k-DAM AN 2A-2 6k l 2限-2 2（反-1）2 点睛：本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求一次函 数、二次函数的解析式，分类讨论是解答问题（2）的关键，求得点M的坐标和点N的坐 标是解答问题（3）的关键.3.如图，某足球运动员站在点O处练习射门，将足球从离地面0.5m的A处正对球门踢出 （点A在y轴上），足球的飞行高度y（单位：制与飞行时间t（单位：s）之间满足函数关系y= at2 + 5t+c,已知足球飞行0.8$时，离地面的高度为3.5m.足球飞行的时间是多少时，足球离地而最高？最大高度是多少？若足球飞行的水平

13、距离x（单位：制与飞行时间t（单位：s）之间具有函数关系x = 10t,己 知球门的高度为2.44m,如果该运动员正对球门射门时，离球门的水平距离为28m,他能 否将球直接射入球门？Q【答案】（1）足球飞行的时间是S时，足球离地而最高，最大高度是4.5m： （2）能.5【解析】试题分析：（1）由题意得：函数y=at2+5t+c的图象经过（0, 0.5） （0.8, 3.5）,于是得到?，求得抛物线的解析式为：y-当2+5是，当t=|时，y»A3.5=0.8 a+5X0.8+c1625、=4.5：251（2）把x=28代入x=10t得t=2.8,当t=2.8时，y=-兼x2.82+5x

14、2.8哈2.25V2.44.于是得 162到他能将球直接射入球门.解：（1）由题意得：函数y=at?+5t+c的图象经过（0, 0.5） （0.8, 3.5）,"0. 5二c «一 & 5二0. 8 &2+5 M 0. g+c '.抛物线的解析式为:y= - >+5t4当，y ma=4.5；(2)把 x=28 代入 x=10t 得 t=2.8,95I.当 t=2.8 时，y=-2.82+5x2.8哈2.25V2.44, 162他能将球直接射入球门.考点：二次函数的应用.4.如图，抛物线y=aX + bx（50）过A （4, 0） , B （1,

15、 3）两点，点C 8关于抛物线 的对称轴对称，过点8作直线8HJ_x轴，交x轴于点H.（1）求抛物线的表达式：（2）直接写出点C的坐标，并求出ABC的面积：（3）点P是抛物线上一动点，且位于第四象限，是否存在这样的点P,使得ASP的而积 为48C而积的2倍？若存在，求出点P的坐标，若不存在，请说明理由：（4）若点M在直线8H上运动，点N在x轴正半轴上运动，当以点C, M, N为顶点的三 角形为等腰直角三角形时，请直接写出此时CM/V的面积.着阳图【答案】（1） y=x2+4x： （2） C （3, 3）,而积为 3： （3） P 的坐标为（5, -5）:（4） 士或52【解析】试题分析：（1）

16、利用待定系数法进行求解即可：（2）先求出抛物线的对称轴，利用对称性即可写出点C的坐标，利用三角形面积公式即可 求面积：（3）利用三角形的而积以及点P所处象限的特点即可求：（4）分情况进行讨论，确定点M、N,然后三角形的面积公式即可求.16a + 4 = 0试题解析：(1)将A (4. 0) , B (1, 3)代入到y=ax?+bx中，得，解a + b = 3a = -1抛物线的表达式为y=-x2+4x.(2) .抛物线的表达式为y=-x2+4x, .抛物线的对称轴为直线x=2.又 C, B 关于对称轴对称，C (3, 3) . /. BC=2tSaabc=-x2x3 = 3.2(3)存在点P

17、.作PQJLBH于点Q,设P (m, -m2+4m).Sa abp = 2S abc> S& abc = 3,S& abp = 6Sa abp + Sa bpq=Sa abh + S 悌形 ahqp6+ x (m 1) x (3 + m24m) = x3x3+ x (34-m 1) (m24m) 222整理得m? - 5m=0,解得mi=0 (舍)，mz=5, .点P的坐标为(5, - 5).4 4) 2或5.2提不：当以M为.宜角顶点，则Sa cmn=彳；)当以N为直角顶点，Sacmn=5;【点睛】本题是二次函数的综合题，主要考查待定系数法求解析式，三角形而积、直角三

18、角形的判定等，能正确地根据题意确定图形，分情况进行讨论是解题的关键.5 .在平面直角坐标系xOy中(如图).已知抛物线y=- ；x?+bx+c经过点A ( - 1, 0)和点B(0, 2),顶点为C,点D在其对称轴上且位于点C下方，将线段DC绕点D按顺时 2针方向旋转90。，点C落在抛物线上的点P处.(1)求这条抛物线的表达式；（2）求线段CD的长：（3）将抛物线平移，使其顶点C移到原点O的位置，这时点P落在点E的位置，如果点D、E、M为顶点的四边形而积为8,求点M的坐标.【答案】抛物线解析式为尸-x P点坐标为（4, ） , D点坐标为（2, 2 9(2).y=- - (x-2) 2+一，

19、2+2x+-； （2）线段CD的长为2； （3） M点的坐 22【解析】【分析】利用待定系数法求抛物线解析式:标为（0,Lx2+2x+±得到关于t 22-），利用抛物线的平移规律确定E点坐标 2为(2, -2),设 M (0, m),当 m>0 时,15利用梯形面积公式得到彳（m+7+2）2=82219（2）利用配方法得到y=- （x-2）则根据二次函数的性质得到C点坐标和抛物9线的对称轴为直线x=2,如图，设CD=t,则D （2, 一 -t）,根据旋转性质得NPDC=90。, 299DP=DC=t,则 P (2+t, - -t),然后把 P (2+t, - - t)代入 y=

20、- 22的方程，从而解方程可得到CD的长：当mVO时，利用梯形面积公式得到,（ -m+*+2）2=8,然后分别解方程求出m即可 得到对应的M点坐标.【详解】（1）把A（-l, 0）和点B（0,=）代入y= - Lz+bx+c得 227 = 25 ， c = .2_l_b+c=O2,解得，c =-2I 5 抛物线解析式为y=- -x2+2x+ -：9，C （2,）,抛物线的对称轴为直线x=2, 29如图，设 CD=t,则 D （2, - - t）, 2,/线段DC绕点D按顺时针方向旋转90。，点C落在抛物线上的点P处， , Z PDC=90°, DP=DC=t,9 . P （2+t,

21、- - t）, 2915159把 P （2+t, - - t）代入 y= - -x2+2x+得-（2+t） 2+2 （2+t） + = - - t, 222222整理得t2-2t=0,解得匕=0 （舍去），t2=2, 线段CD的长为2；95（3） P点坐标为（4, -） , D点坐标为（2,-）,229:抛物线平移，使其顶点C （2,-）移到原点。的位置，9，抛物线向左平移2个单位，向下平移二个单位,99而P点（4,-）向左平移2个单位，向下平移一个单位得到点E,22.E点坐标为（2, -2）,设 M （0, m）,1 577当m>0时，一（m+ +2）2=8,解得m二一，此时M点坐标为

22、（0,）：2 222I577当m<0时，一（ - m+ +2 ）2=8,解得m二-,此时M点坐标为（0,-）； 222277综上所述，M点的坐标为（0, 三）或（0,-）.22【点睛】本题考查了二次函数的综合题，涉及到待定系数法、抛物线上点的坐标、旋转的 性质、抛物线的平移等知识，综合性较强，正确添加辅助线、运用数形结合思想熟练相关 知识是解题的关键.6.在平面直角坐标系xOy中，已知抛物线的顶点坐标为（2, 0）,且经过点（4, 1）,如图，直线y=与抛物线交于A、B两点，直线I为y=-l. 4（1）求抛物线的解析式：（2）在I上是否存在一点P,使PA+PB取得最小值？若存在，求出点P

23、的坐标：若不存 在，请说明理由.（3）知F （xo, y。）为平面内一定点，M （m, n）为抛物线上一动点，且点M到直线I的 距离与点M到点F的距离总是相等，求定点F的坐标.【答案】（I）抛物线的解析式为y=：x2-x+l. （2）点P的坐标为（或，-1） . （3）413定点F的坐标为（2, 1）.【解析】分析:（1）由抛物线的顶点坐标为（2, 0）,可设抛物线的解析式为y=a （x-2） 2,由抛 物线过点（4, 1）,利用待定系数法即可求出抛物线的解析式：（2）联立直线AB与抛物线解析式成方程组，通过解方程组可求出点A、B的坐标，作点 B关于直线I的对称点孔 连接AB，交直线I于点P,

24、此时PA+PB取得最小值，根据点B的 坐标可得出点夕的坐标，根据点A、的坐标利用待定系数法可求出直线AB，的解析式，再 利用一次函数图象上点的坐标特征即可求出点P的坐标：（3）由点M到直线I的距离与点M到点F的距离总是相等结合二次函数图象上点的坐标特征，即可得出（l-yo）m2+ （2-2x0+2y0） m+x02+yo2-2y0-3=0,由m的任意性可得出关 2 2于x。、y。的方程组，解之即可求出顶点F的坐标.洋解：（1） .抛物线的顶点坐标为（2, 0）,设抛物线的解析式为y=a （x-2） 2.该抛物线经过点（4, 1）,l=4a,解得：a=,4,抛物线的解析式为（x-2） 2=；x2

25、-x+l.44（2）联立直线AB与抛物线解析式成方程组，得：1十,解得：y=-x2 -x + lL 4 二点A的坐标为（1, L）,点B的坐标为（4, 1）.4作点B关于直线I的对称点BS连接AB，交直线I于点P，此时PA+PB取得最小值（如图1点B'的坐标为（4, -3）.设直线AB'的解析式为y=kx+b （HO）,12将 A （1, L）、B（4,3）代入 y=kx+b,得: 4k+b=- 44k+b=-313 4 直线AB，的解析式为y=-jx+,t , 13 4当y=-l时，有x+ =1, 12 328解得：*=看，点P的坐标为（=，-1）. 13（3） .点M到直线

26、I的距离与点M到点F的距离总是相等,（m-xo） 2+ （n-yo） 2= （n+1） 2,m2-2xom+xo2-2yon+yo2=2n+l,M （m, n）为抛物线上一动点，1 ,n= m-m+1, 4/. m2-2xom+xo2-2yo ( m2-m+l) +y02=2 ( m2-m+l) +1, 44整理得：(1- - yo)m2+ (2-2x0+2y0) m+xo2+yo2-2yo-3=O.2 2m为任意值，乙 乙2 2% + 2 yo=0xo' + >o- - 2%-30 ./=2）0=1，定点F的坐标为（2, 1）.点睛：本题考查了待定系数法求二次（一次）函数解析式

27、、二次（一次）函数图象上点的 坐标特征、轴对称中的最短路径问题以及解方程组，解题的关键是：（1）根据点的坐标, 利用待定系数法求出二次函数解析式；（2）利用两点之间线段最短找出点P的位置：（3）根据点M到直线I的距离与点M到点F的距离总是相等结合二次函数图象上点的坐 标特征，找出关于x。、y。的方程组.7.如图，已知抛物线丁 =+公+ C的顶点为A（4,3）,与轴相交于点3（0,_5）,对称轴为直线/,点例是线段A8的中点.（2）写出点M的坐标并求直线A3的表达式；（3）设动点尸，。分别在抛物线和对称轴I上，当以A，P，Q,例为顶点的四边形是 平行四边形时，求。，。两点的坐标.【答案】（1）

28、y = -1x2+4x-5； （2）y = 2x-5. （3）点夕、。的坐标分别为（6,1）或（2）、（4,3）或（4）.【解析】【分析】(1)函数表达式为：)，= (x = 4+3,将点3坐标代入上式，即可求解：(2) A(4,3)、B(0,-5),则点M(2,l),设直线A8的表达式为：y = kx-5,将点 4坐标代入上式，即可求解；(3)分当AM是平行四边形的一条边、AM是平行四边形的对角线两种情况，分别求解 即可.【详解】解：(1)函数表达式为：y = a(x = 4+3,将点4坐标代入上式并解得：a = -,2故抛物线的表达式为：y = -ix2+4.r-5；(2) 4(4,3)、

29、5(0-5),则点M(2,-1),设直线48的表达式为：y =丘一5,将点A坐标代入上式得：3 = 4左一5,解得：k = 2,故直线A8的表达式为：y = 2x-5.(Jx(3)设点。(4,s)、点P m,-nr +4m-5 , I2/当AM是平行四边形的一条边时，点A向左平移2个单位、向下平移4个单位得到M，同样点P；+4?一5)向左平移2个单位、向下平移4个单位得到2(4,5),即： m-2 = 4, -nr +46-5 4 = $ ,2解得：in = 6» 5 = 3»故点尸、。的坐标分别为(6,1)、(4,-3)；当AM是平行四边形的对角线时，由中点定理得：4 +

30、 2 = 777 + 4, 3-1 =+4/72-5 + 5 t2解得：m = 2 , 5 = 1»故点、P、。的坐标分别为(2,1)、(4,1)；故点P、。的坐标分别为(61), (4,3)或(2,1)、(4,-3), (2,1)或(4,1).【点睛】本题考查的是二次函数综合运用，涉及到一次函数、平行四边形性质、图象的面积计算 等，其中(3),要主要分类求解，避免遗漏.13y = ' x + 28.抛物线 42 与x轴交于A, B两点(OAVOB),与y轴交于点C.(1)求点A, B, C的坐标：(2)点P从点O出发，以每秒2个单位长度的速度向点B运动，同时点E也从点。出

31、发,以每秒1个单位长度的速度向点C运动，设点P的运动时间为t秒(0<t<2).1 1过点E作x轴的平行线，与BC相交于点D (如图所示)，当t为何值时，0P 前的值 最小，求出这个最小值并写出此时点E, P的坐标;%C K/在满足的条件下，抛物线的对称轴上是否存在点F,使4EFP为直角三角形？若存在，请直接写出点F的坐标：若不存在，请说明理由. 1 1 + -【答案】(1)A (2, 0) , B (4, 0) , C (0, 2) ： (2)时，0P 七。有最小值1,此时 OP=2, OE=1, E (0, 1) , P (2, 0) ； F (3, 2) , (3, 7).【解

32、析】试题分析：(1)在抛物线的解析式中，令y=o,令x=o,解方程即可得到结果；CE ED 2-t DE (2)由题意得：0P=2t, OE=t,通过 CDE- CBO得到,° °匕KP 24 ,求得1 1丽 丽有最小值1,即可求得结果：存在，求得抛物线的对称方程为x=3,设F (3, m),当AEFP为直角三角形时，当 NEPF=90。时，当NEFP=90。时，当N PEF=90。时，根据勾股定理列方程即可求得结 果.13产2%+2 = 0试题解析：(1)在抛物线的解析式中，令y=0,即42,解得：勺一2,“2 = 4,oaVOB,A (2, 0) , B (4, 0),

33、在抛物线的解析式中，令x=0,得y=2. C (0, 2)：CE ED =(2)由题意得：0P=2t, OE=t, ； DEII OB, CDE- CBO,即2-t DE24 ,DE=4 - 2t,111 1 1 1A OP + EDjt + 432t=-t2 + 2t=l-(t-l)2, .0<1<2,1-("1)2始终为正数，且 t=l1 1 1时，有最大值1,.=1时，1T" 1产有最小值1,即t=l时，丽 前有最小 值 1,此时 OP=2, OE=1, E (0, 1) , P (2, 0)：13y = _汽2 K + 2存在，.抛物线一4 2的对称轴方

34、程为x=3,设F (3, m) , .EP2 = 5,PF2=(3-2)2+m2, EF2=(7n-l)2 + 32f当 EFP为直角三角形时，当NEPF=9。时，EP2 + PC = EF2,即5+ (3-2尸 +m2 =("一1)2 + 32,解得：必:2, 当NEFP=90°时,"2 +？2 = £22,即(771-1)2 + 32 + (3-2)2 + 血2 = 5,解得：m=0 或m=l,不合题意舍去，.当NEFP=90。时，这种情况不存在，当NPEF=9。时，"2 + PE2 = PF2,即 - 1尸 + 3? + 5 = (3 -

35、 2尸 + 小，解得：;7, 综上所述，F(3, 2) , (3, 7).考点：1.二次函数综合题；2.动点型；3.最值问题：4.二次函数的最值：5.分类讨 论：6.压轴题.9.如图，已知二次函数y=ax?+bx+3的图象交x轴于点A (1, 0) , B (3, 0),交y轴于 点C.(1)求这个二次函数的表达式：(2)点P是直线BC下方抛物线上的一动点，求 BCP而积的最大值；(3)直线x=m分别交直线BC和抛物线于点M, N,当 BMN是等腰三角形时，宜接写出【答案】(1)这个二次函数的表达式是y=x2-4x+3； (2) Sabcp»a=: (3)当aBIVIN 8是等腰三角

36、形时，m的值为"，-四, 1, 2.【解析】分析：(1)根据待定系数法，可得函数解析式：(2)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得PE的长，根据面积的和差，可得二次函数，根据二次函数的性质，可得答案：(3)根据等腰三角形的定义，可得关于m的方程，根据解方程，可得答案.详解：(1)将A (1, 0) , B (3, 0)代入函数解析式，得。+ + 3=09a + 3b + 3=0a=b=-4 这个二次函数的表达式是y=x<4x+3：(2)当 x=0 时，y=3,即点 C (0, 3),代入函数解析式，得设BC的表达式为y=kx+b,将点B (3, 0

37、)点C (0, 3) '3k+b=0b=0'解这个方程组，得k=-'b=3 *直线BC的解析是为y=-x+3,交直线BC于点E (t,t+3), PE=-t+3- (t2-4t+3) =-t2+3t,.'.Sa bcp=Sa bpe+Scpe= ( -t2+3t) x3=- ( t- ) 2+,2 2283 山 3 l27- - - H t= ll't, Sabcpi大工2 283 3) M (m, -m+3) , N (m, m2-4m+3)MN=m2-3m* BM=>/2当 MN=BM 时，(l)m2-3m=/2(m-3),解得 m= & , (2)m2-3m-y/2(m-3),解得 m二-人当 BN=MN 时，Z NBM=Z BMN=45°, m2-4m+3=0t 解得 m=l 或 m=3 (舍)当 BM=BN 时,Z BMN=Z BNM=45°,-（m2-4m+3） =-m+3,解得 m=2 或 m=3 （舍）,当 BMN是等腰三角形时，m的值为点, -JI，1, 2.点睛：本题考查了二次函数综合题，解（1）的关键是待定系数法；解（2）的关键是利