数字信号处理-原理与实践(方勇)习题答案三章全

1、第一章 数字信号处理基本概念第一章习 题1-1 有一个连续信号，式中，（） 求出的周期；（） 用采样间隔对进行采样，写出采样信号的表达式；（） 画出对应的时域离散信号（序列）的波形，并求出的周期。解：（1）的周期是（2） （3）的数字频率为，周期。 ，画出其波形如题1-1图所示。 题1-1图1-2 设，其中为采样周期。（1）信号的模拟频率为多少？（2）和的关系是什么？（3）当时，的数字频率为多少？解：（1）的模拟频率。（2）和的关系是：。（3）当时，。1-3 判断下面的序列是否是周期的，若是周期的，确定其周期。（1），为常数；（2）。解： （1），这是有理数，因此是周期序列，周期是；（2），这

2、是无理数，因此是非周期序列。1-4 研究一个线性时不变系统，其单位脉冲响应为指数序列，。对于矩阵输入序列，求出输出序列，并用MATLAB计算，比较其结果。分析：输入，线性时不变系统的输出等于输入序列与单位脉冲响应的卷积，用公式表示为为了计算输出序列的第个值，必须计算出乘积，并将所得到的序列值相加。解：输出序列可以分成三种情况来求解：（） 当时，由于和的非零取样互不重叠，因此。（） 当时，从到，和的非零取样值有重叠，因此 （） 当时，和重叠的非零取样值从到，因此 所以 利用MATLAB求其响应,程序如下：a=1/2;N=20;n=0:N-1;c=1;d=1 -a;x=ones(1,N);y=fi

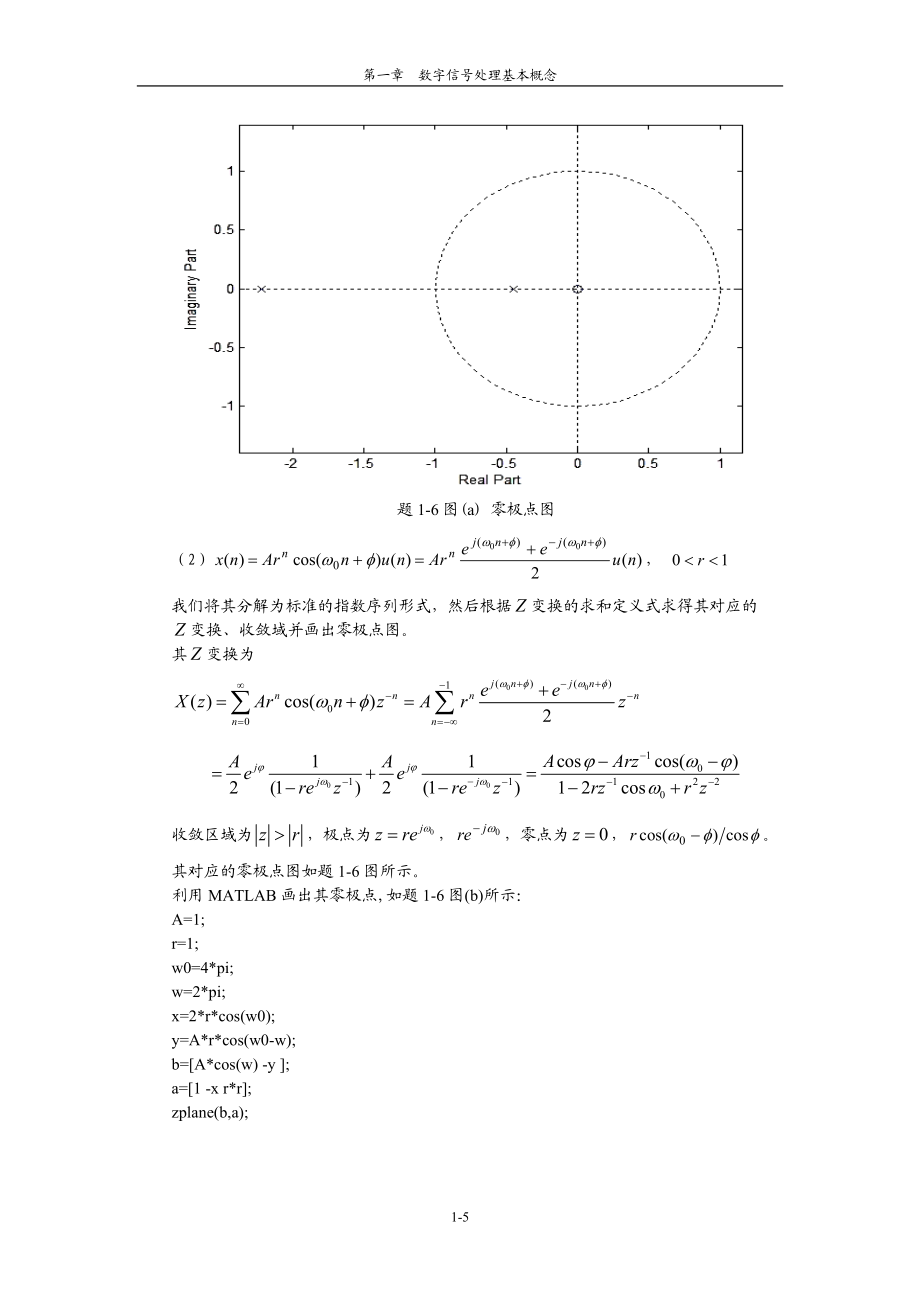
3、lter(c,d,x);stem(n,y);ylabel('y(n)');题1-4图 输出相应序列1-5 设，求。解： ，所以， ，其Z反变换为显然，在处，的极点被的零点所抵消，如果，则的收敛域比与收敛域的重叠部分要大。1-6 求下列序列的变换及其收敛域，并用MATLAB画出零极点示意图。（） 双边指数序列，；（） 正弦调制序列，。解：（1）双边指数序列可写为其变换为 ，是一个双边序列，其收敛域为表示极点，极点为，零点为。其极点、零点图如图所示，图中表示极点，表示零点。利用MATLAB画出其零极点，如题1-6图(a)所示：a=3;y=1-a*a;b=0 y 0;a=-a y -

4、a;zplane(b,a);题1-6图(a) 零极点图（2）， 我们将其分解为标准的指数序列形式，然后根据变换的求和定义式求得其对应的变换、收敛域并画出零极点图。其变换为收敛区域为，极点为，零点为，。其对应的零极点图如题1-6图所示。利用MATLAB画出其零极点,如题1-6图(b)所示：A=1;r=1;w0=4*pi;w=2*pi;x=2*r*cos(w0);y=A*r*cos(w0-w);b=A*cos(w) -y ;a=1 -x r*r;zplane(b,a);题1-6图(b) 零极点图讨论 通常将正弦序列信号展开为两个基本复指数序列和或差的形式，然后按照变换定义式求起对应的变换和收敛域。

5、对于变换表达式可表示为等比级数和的形式的序列，其变换的收敛域是保证等比小于1，如本例中要保证，可得收敛域为。题1-6图 零极点示意图1-7 已知， 求其变换及其收敛域。并用MATLAB求解。解：这是一个双边序列，其变换为，MATLAB求解程序如下： F=ztrans(sym('ak+bk') 结果为：F =- z/(a - z) - z/(b - z)1-8 求,的逆变换，并用MATLAB求解。解：由部分分式展开可得 , 因为。所以得MATLAB求解：程序如下：syms k z;Fz=5*z/(z2+z-6);fk=iztrans(Fz,k)运行结果：fk =2k - (-3)

6、k1-9 判断系统（1），（2）是否为时不变系统，并利用MATLAB验证。解：（1）令输入为，输出为而，所以系统是时变的。MATLAB验证：令 ，程序如下：x=1 2 1;n0=1;n=-1:1;x0=2 1;%x0为x横坐标非负的值y=cumsum(x0);Y=cumsum(x);subplot(3,2,1);stem(n,x);xlabel('n');ylabel('x(n)');title('输入');axis(-1,3,0,4);subplot(3,2,2);n=0:1;stem(n,y);xlabel('n');ylab

7、el('y(n)');title('输出');axis(-1,3,0,4);subplot(3,2,3);n=0:2;stem(n,x);xlabel('n');ylabel('x(n-n0)');title('输入');axis(-1,3,0,4);subplot(3,2,5);n=0:2;stem(n,Y);xlabel('n');ylabel('Y(n)');title('输出');axis(-1,3,0,4);subplot(3,2,4);n=1:2;stem

8、(n,y);xlabel('n');ylabel('y(n-n0)');title('输出');axis(-1,3,0,4);题1-9图(a) 时变性验证（2）令输入，输出而，所以系统为时变的。MATLAB验证：令，程序如下：x=1 2 1;n0=1;for i=1:length(x) y(1,i)=i*x(1,i);endfor i=1+n0:length(x)X(1,i+n0)=x(1,i);endfor i=1+n0:length(x)+n0y_(1,i)=(i-n0)*x(1,i-n0);endfor j=1:length(x) Y(1,

9、j)=j*X(1,j);endsubplot(3,2,1);n=1:3;stem(n,x);xlabel('n');ylabel('x(n)');title('输入');axis(0,4,0,6);subplot(3,2,2);stem(n,y);xlabel('n');ylabel('y(n)');title('输出');axis(0,4,0,6);subplot(3,2,3);n=1:4;stem(n,x_);xlabel('n');ylabel('x(n-n0)'

10、;);title('输入');axis(0,4,0,6);subplot(3,2,5);stem(n,Y);xlabel('n');ylabel('Y(n)');title('输出');axis(0,4,0,6);subplot(3,2,4);n=1:4;stem(n,y_);xlabel('n');ylabel('y(n-n0)');title('输出');axis(0,4,0,6);题1-9图(b) 时变性验证1-10 利用MATLAB验证例题1-27（1）中的系统是否为线性时不

11、变系统。解：令输入为，则输出为，而，所以，系统为时不变系统。又因为 而，所以系统为非线性系统。MATLAB验证：: 时变性验证：令，程序如下：a=1;b=2;p=2;q=3;n0=1;x=1 2 3;y=a*x+b;for i=1:size(x,2)x_(1,i+n0)=x(1,i);y_2(1,i+n0)=y(1,i);endx_=zeros(1:n0),x_(n0+1:end);y_1=a*x_+b;y_1=zeros(1:n0),y_1(n0+1:end);subplot(3,2,1);n=0:2;stem(n,x);xlabel('n');ylabel('x(n

12、)');title('输入');axis(0,4,0,6);subplot(3,2,2);n=0:3;stem(n,x_);xlabel('n');ylabel('x(n-n0)');title('输入');axis(0,4,0,6);subplot(3,2,3);n=0:2;stem(n,y);xlabel('n');ylabel('y(n)');title('输出');axis(0,4,0,6);subplot(3,2,4);n=0:3;stem(n,y_1);xlabe

13、l('n');ylabel('Y(n)');title('输出');axis(0,4,0,6);subplot(3,2,5);n=0:3;stem(n,y_2);xlabel('n');ylabel('y(n-n0)');title('输出');axis(0,4,0,6);题1-10图(a) 时变性验证: 线性验证：令，,程序如下：x1=1 2 3 2;x2=3 2 1 1;a=1;b=2;p=2;q=1;n=0:3;y1=a*x1+b;y2=a*x2+b;Y1=a*(x1*p+q*x2)+b;Y2

14、=p*y1+q*y2;subplot(1,2,1);stem(n,Y1);xlabel('n');ylabel('Y1(n)');axis(0,3,0,14);subplot(1,2,2);stem(n,Y2);xlabel('n');ylabel('Y2(n)');题1-10图(b) 线性性验证111 已知系统函数，试用MATLAB画出该系统的幅频特性。解： 利用MATLAB中的freqz()函数可以画出该系统的幅频特性曲线，如题1-11图所示。 取10。MATLAB程序如下：N=10;b=1 zeros(1,N-1) 1;a=

15、1 zeros(1,N);OMEGA=0:pi/150:2*pi;H=freqz(b,a,OMEGA);plot(OMEGA,abs(H);题1-11图 幅频响应特性1-12 一般的滑动平均由下列方程定义 该系统计算输出序列的第个样本时是将其作为输入序列第个样本前后的个样本的平均。求：（1）该系统的冲激响应； （2）求该系统的频率响应； （3）对，求和，并用MATLAB画出其图形。解： （1）（2）因为 因此频率响应就是利用等比级数求和公式 可以得到：（3）当，时，利用MATLAB画出其频率响应图：由 得 所以MATLAB程序如下：M1=0;M2=4;X=1/(M1+M2+1);b=X zer

16、os(1,M2) -X;a=1 -1;OMEG=-pi:pi/100:pi;H=freqz(b,a,OMEG);subplot(2,1,1),plot(OMEG,abs(H);subplot(2,1,2),plot(OMEG,180/pi*unwrap(angle(H);运行结果如题1-12图所示：题1-12图 频率响应曲线图1-13 设某线性时不变离散系统的差分方程为，试求它的单位脉冲响应。并讨论其因果性和稳定性，并用MATLAB计算，与理论值进行比较。解：对上式两边取变换，得到：极点：，当ROC：时，系统因果不稳定，；当ROC：时，系统非因果稳定，；当ROC：时，系统非因果不稳定，。1-1

17、4 给定下述系统的差分方程，试判定系统是否是因果、稳定系统，并说明理由，如果是稳定系统，通过MATLAB画出其零极点图。（1）（2）（3）解： （1）只要，该系统就是因果系统，因为输出只与时刻的和时刻以前的输入有关。如果，因此系统是稳定系统。MATLAB画出零极点,如题1-14图(a)所示：N0=100;X=N0-1;b=1 zeros(1,X-1) -X;a=1 -1;zplane(b,a);题1-14图(a) 零极点示意图（2）该系统是非因果系统，因为时刻的输出还和时刻以后的输入有关。如果，则，因此系统是稳定系统。MATLAB画出零极点图如下：b=1 1;a=1 0;zplane(b,a)

18、;题1-14图(b) 零极点示意图（3）系统是非因果系统，因为时刻输出和时刻以后的输入有关。如果，因此系统是稳定的。1-15 求下列单位脉冲响应的变换及收敛域，用MATLAB画出零极点分布图。 （1）、 （2）、 （3）、解：（1）由变换的公式可得其变换为：=，。利用MATLAB画出其零极点，程序及运行结果如题1-15图(a)所示：b=1 0;a=1 -0.2;zplane(b,a);题1-15图(a) 零极点示意图（2）利用变换公式可得：其变换为, MATLAB画出零极点如下题1-15图(b)所示：w0=2*pi;x=exp(j*w0);b=1;a=1 -x;zplane(b,a);题1-1

19、5图(b) 零极点示意图（3） 因为，由（2）知的变换为 的变换为所以得出的变换经化简得： , 利用MATLAB画出其零极点如下题1-15图(c)所示: w0=pi/4;b=1 -cos(w0);a=1 -2*cos(w0) 1;zplane(b,a);题1-15图(c) 零极点示意图1-16 已知系统函数如下：，用MATLAB编程判断系统是否稳定.解： MATLAB程序如下：A=2 -2.9 0.1 2.3 -1.5P=roots(A);M=max(abs(P);if(M<1) disp('系统稳定')else disp('系统不稳定')end运行结果如

20、下：A = 2.0000 -2.9000 0.1000 2.3000 -1.5000系统稳定1-17 设一因果LTI系统的差分方程为 并且已知初始条件为，输入，利用MATLAB求系统的输出。解：%用迭代法求取10点数据y=zeros(1,10);i=1:10;y(1)=-2-3+1;y(2)=2*y(1)+3+1+4;y(3)=2*y(2)-3*y(1)+1+5+4*0.2;y(4)=2*y(3)-3*y(2)+4*0.22;for n=5:10 y(n)=2*y(n-1)-3*y(n-2)+4*0.2(n-2);endstem(i-1,y);xlabel('n');ylabe

21、l('y(n)');结果如题1-17图所示：题1-17图 输出响应1-18 一系统的差分方程描述如下：试确定该系统的频率响应，并求出输入序列为的稳态输出。解：由差分方程可得出， 其特征根为，所以该系统为一稳定系统。当输入序列为时，由稳态输出的定义，我们可以计算出：，。所以其稳态输出为 用MATLAB画出其频率响应:程序如下：b=1 0 -1;a=1 0 0.81;OMEG=-pi:pi/100:pi;H=freqz(b,a,OMEG);subplot(2,1,1),plot(OMEG,abs(H);subplot(2,1,2),plot(OMEG,180/pi*unwrap(a

22、ngle(H);运行结果:题1-18图 频率响应曲线1-19 考虑一个三阶系统输入，初始状态，和，利用状态方程方法求出。解： 定义，差分方程可以写为如下状态方程的形式：可计算出，。其MATLAB程序如下：%状态方程求解系统响应演示程序A=0 1 0;0 0 1;-0.8 0.2 0.4;B=0;0;5;C=-0.8 0.2 0.4;D=5;q0=5;4;2;n=0:1:25;X=ones(size(n)'Y, s=dlsim(A,B,C,D,X,q0);stem(n,y);xlabel('n');ylabel('y(n)');grid;题1-19图 输出

23、响应第二章21 试求如下序列的傅里叶变换：（1）（2）（3）（4）（5）（6）解： （1） （2） （3）， （4）= （5） （6） 22 设信号，它的傅里叶变换为，试计算(1)（）（）。解： （）（），（）23 已知求的逆傅里叶变换。解：24 设和分别是和的傅里叶变换，试求下面序列的傅里叶变换。（1）（2）（3）（4）解：(1) ， 令则：(2)(3)，令，则： (4) 由，得所以 25 已知序列，求其傅里叶变换DTFT。解：26 设，试求的共轭对称序列和共轭反对称序列；并分别用图表示。解： 图形如下题2-6图所示：题2-6图 与序列图27 设系统的单位脉冲响应，输入序列为完成下面各题：（

24、1） 求出系统输出序列；（2） 分别求出、和的傅里叶变换。解：（1）（2） 28 若序列是因果序列，其傅里叶变换的实部如下式： 求序列及其傅里叶变换。解：29 试用定义计算周期为5，且一个周期内的序列的DFS。解：210 求出周期序列的DFS。 解：由题知周期为4 211 已知周期为的信号，其DFS为，证明DFS的调制特性。证明： 命题得证。212 设将以4为周期进行周期延拓，形成周期序列，画出和的波形，求出的离散傅里叶级数和傅里叶变换。解： 以4为周期。 和波形图如下题2-12图所示：题2-12图 和波形图213 如果是一个周期为的周期序列，其DFS为，将看作周期为2的周期序列，其DFS为。

25、试利用确定。解： 按照题意，可以写出： = + 令，则 + 所以 214 根据下列离散时间信号的傅里叶变换，确定各对应的信号。（1）（2）解： （1） 因此（2）因为含有冲激函数，因此，对应的信号为周期信号，设为，其周期为，DFS为，则有：的DTFT，有 即 而已知可见即所以，得是以为周期的周期函数。215 计算以下诸序列的点DFT，在变换区间内，序列定义为（1） （2），（3） （4）,其中（5） ，其中解： （1）（2）（3）， （4） 由DFT的定义直接计算序列的DFT，对变换采样。由于，对 在， 上采样，求得: （5） =,216 已知，求其点DFT。解: ，217 设，求其原序列。解

26、： 218 已知下列，求，其中。解：219 已知序列的4点离散傅里叶变换为，求其复共轭序列的离散傅里叶变换。解：220 证明DFT的对称定理，即假设证明： 证明： 221 如果，证明DFT的初值定理证明：由IDFT定义式知222 证明离散帕斯维尔定理。若，则证明： 223 令表示点序列的点离散傅里叶变换。本身也是个点序列。如果计算的离散傅里叶变换得一序列，试用求。解：按照题意，可以写成 因为 所以 224 一个长度为8的有限时宽序列的8点离散傅里叶变换，如题2-24图所示。 令题2-24图 求的16点DFT，并画出其图形。解：按照题意，当为奇数时为零，故可写出而 所以 即所以的图形如题2-26

27、（a）图所示：题2-26（a）图225 已知序列是的6点DFT。（1） 若有限长序列的6点DFT 是,求。 （2） 若有限长序列的3点DFT 满足，求。解： （1）序列的DFT由的DFT与复指数相乘组成，这相当于是将圆周移位了4点：，所以：（2）序列长度为3，DFT变换为，其中是 的6点DFT。由于系数是对在单位圆上等间隔采样6点的结果，所以，相当于是对在单位圆上等间隔采样3点，所以在区间外,因而;就得到。226 在很多实际应用中都需要将一个序列与窗函数相乘。设是一个点的序列，是汉明窗：试用的DFT求加窗序列的DFT。解：首先用复指数表示汉明窗因此如果则所以加窗序列的DFT为227 已知求和；

28、欲使两卷积相同，则循环卷积的长度的最小值应为多少？解： ， L=4+2-1=5 228 已知序列，若是与它本身的4点循环卷积，求及其4点的。解：的4点： 229 和都是长度为6点的有限长序列，和分别是和的8点DFT。若组成乘积，对作8点IDFT得到序列，问在哪些点上等于以下线性卷积：解： 和都是长度为6点，则的长度为11点，而为 与的8点循环卷积。根据线性卷积与循环卷积的关系，8点的循环卷积中，前3个点将由线性卷积的叠加，而后5个点等于线性卷积。230 序列 （1） 求的4点DFT；（2） 若是与它本身的4点循环卷积，求及其4点DFT；（3） ，求与的4点循环卷积。解： 由题可知：（1） （2

29、） 得到 即 （3）由题知 得 231 序列为 计算的5点DFT，然后对得到的序列求平方：求的5点DFT反变换。解：序列的5点DFT等于乘积，所以是与本身5点圆周卷积的结果： 一个简单的计算圆周卷积的方法是先进行线性卷积，然后将结果叠加： 与本身的线性卷积的结果为 用表格法计算圆周卷积，就会得到 题2-31表0 1 2 3 45 6 74 4 1 4 20 1 00 1 0 0 0 0 0 04 5 1 4 2 所以232 考虑两个序列：若组成，其中、分别是和的5点DFT，对作DFT反变换得到序列，求序列。解： 因为是两个5点DFT和的乘积，所以是和的5点圆周卷积。可以用图解法计算圆周卷积，也

30、可以用先线性卷积再重叠的方法，还可以用先将DFT相乘再对乘积作DFT反变换的方法。本题中，是一个简单序列，我们可以用分析法。和的5点圆周卷积是： ，因为，且，5点圆周卷积是： ，圆周卷积等于圆周移位序列的值从到求和的结果，因为是（可以看作是长度为5 的序列）可以通过反向读取序列得到，从开始：是的前5个 值相加的结果，得到。将此序列圆周右移1后，就有前4个值相加后得到。继续求解，求得：,。233 两个有限长序列和的零值区间为;。对每个序列作20点DFT，得和，如果，。，。试问在哪些点上？为什么？解： 设，而，的长度为27，的长度为20，且 当上述周期延拓序列中无混叠的点上有：，234 两个有限长

31、序列和，在区间以外的值为，两个序列圆周卷积后得到的新序列为其中。若仅在时有非零值，确定为哪些值时，一定等于和的线性卷积？解： 由于，等于和的线性卷积的点是在区间内，圆周移位等于线性移位的那些点。由于仅仅在区间内有非零值，我们可以看到杂区间内。所以当时线性卷积与圆周卷积相等。235 求证循环卷积定理。设有限长序列和的长度分别为和，取，且和分别是两个序列的点DFT。（1） 若，求证；（2） 若，求证：。证明：（1）点DFT等于的序列为:, ,需要用和来表示，由于， 将代入到的表达式中，有：，, ,交换求和顺序，则，, ,括号内的项等于，有：，, , =（2） 由定义， 。若想用和 来表示，将下面的

32、表达式代入上式得：，交换求和顺序，上式变成： 第二个求和就是，有： 所以，是和圆周卷积的倍： 问题得证。236 若和都是长为点的序列，和分别是两个序列的点DFT。证明： 证明：令和分别是和的点DFT ，是的点DFT，则的DFT是，由性质有 ，让计算，就可以得到结论：237 已知实序列的点DFT前个值为求其余三点的值。解：为实序列，满足共轭对称性，得其余三点： , 0 238 已知、是长度为4的实序列， ，求序列，。解：由，得：， 所以由上知 综上可得：，239 已知序列是的6点DFT， 若有限长序列的6点DFT等于的实部，即，求。 解： 的实部是，为了计算的DFT反变换，我们需要计算的DFT反

33、变换。由于是的DFT，所以的DFT反变换是：，所以为：240 如何用一个点DFT变换计算两个实序列和的点DFT变换？解： 两个实序列的DFT可以由一个点DFT求得：首先，我们组成一个点复序列计算的点DFT后，利用DFT的共轭对称性质从中提取出和。实序列的DFT有共轭对称性： 虚序列的DFT有共轭反对称性：由于 是实序列的DFT：这是的共轭对称部分。同样，是虚序列的DFT： 这是的共轭反对称性。241 一个有限长序列，设其变换是。如果在，点上对采样，就得到一组DFT系数。求4点DFT等于这些采样值的序列。解：对在单位圆上等间隔采样4点将造成的混叠： 利用表格法计算上式中的求和，注意只有序列和在时

34、有非零值，所以有题2-41表0 1 2 34 5 6 7 1 1 1 11 1 0 0 1 1 0 00 0 0 0 2 2 1 1 242 设，试画出时域基2FFT流图，并根据流图计算每个碟形运算的结果，最后写出的序列值。解： 2FFT流图如题2-42图所示：题2-42图 时域基2FFT流图 243 已知序列=，用FFT蝶形运算方法计算其8点的DFT。画出计算流图，标出各节点数值。解： 用点DFT计算点的DFT 计算8点的DFT所以其计算流图如题2-43图所示：题2-43图 FFT蝶形运算流图244 设序列的长度为200，对其用时域基2FFT来计算DFT，请写出第三级蝶形中不同的旋转因子。解

35、: 由于序列的长度为200，所以取,得。又因为，第3级蝶形运算中不同的旋转因子为： ， ， ，245 如果通用计算机的速度为平均每次复数乘需要，每次复数加需要，用来计算点DFT，问直接计算需要多少时间。用FFT计算呢？照这样计算，用FFT进行快速卷积对信号进行处理时，估算可实现实时处理的信号最高频率。解： 当时，直接计算DFT的复数乘法运算次数为次直接计算1024点DFT需要时间为s用FFT计算1024点DFT所需计算时间为 快速卷积时，要计算一次点FFT（考虑到已计算好存入内存），一次点IFFT和次频域复数乘法。所以，计算1024点快速卷积的计算时间约为 所以，每秒钟处理的采样点数（即采样速

36、率）次/秒。由采样定理知，可实时处理的信号最高频率为 应当说明，实际实现时， 还要小一些。这是由于实际采样频率高于奈奎斯特速率，而且在采用重叠相加法时，重叠部分要计算两次。重叠部分长度与长度有关，而且还有存取数据指令周期等。246 序列长240点，长10点。当采用直接计算法和快速卷积法（用基2FFT）求它们的线性卷积时，各需要多少次乘法？解： （1）已知直接线性卷积复乘的次数为 （次）（2）因为取。快速卷积中复乘的次数： 1），需次复乘； 2），需次复乘； 3），需次复乘； 总的复乘的次数为：(次)247 设有限长序列的DFT为，我们可使用FFT来完成该运算.现假设已知，,如何利用FFT求原序

37、列。解： ， 因此，利用FFT求的步骤为：(1) 对求共轭(2) 对进行FFT变换(3) 对变换后的序列取共轭，并乘以即得到。248 已知和是两个点实序列和的DFT，若要从和求和，为提高运算效率，试设计用一次点IFFT来完成。解： 为实序列。为共轭对称序列，为共轭反对称序列。将，作为序列的共轭对称分量和共轭反对称分量计算一次点IFFT得到由DFT的共轭对称性，249 设是长度为的有限长实序列，为的点DFT。（1） 试设计用一次点DFT完成计算的高效算法。（2） 若已知，试设计用一次点IDFT实现求的点IDFT运算。解： 本题的解题思路就是DIF-FFT思想（1） 在时域分别抽取偶数点和奇数点得

38、到两个点实序列和根据DIT-FFT思想，只要求得和的点DFT，再经过简单的一级碟形运算就可以得到的2点DFT。又为实，所以根据DFT的共轭对称性，可用一次点DFT求得和，方法如下：令则2点可由、得到 这样通过一次点DFT计算完成2点DFT（2） 设,则过程如下由计算出，由，构成点频域序列其中，进行点IDFT得到由DFT的共轭对称性由和定义得。250 一个3000点的序列输入一个线性时不变系统，该系统的单位脉冲响应长度为60。为了利用快速傅里叶变换算法的计算效率，该系统用128点的离散傅里叶变换和离散傅里叶反变换实现。如果采用重叠相加法，为了完成滤波器运算，需要多少DFT？解： 采用重叠相加法，

39、将分成若干个长度为的不重叠的序列。若的长度为，则的长度为，所以DFT变换的长度。由题设，必须分成长度为的序列： 的长度为3600点，所以共有44个序列（其中最后一个序列仅有33个非零值）。为了计算卷积共需要：1 一个DFT用于计算。2 44个DFT用于的计算。3 44个用于 IDFT变换的计算。一共需要45个DFT变换和44个IDFT变换。2-51 已知信号，用DFT分析信号的频谱。解：利用MATLAB分析信号的频谱画出频谱图如题2-51图所示：N1=128;N2=512;ws=100;w1=10;w2=12;fs=ws/(2*pi);n1=0:N1-1;n2=0:N2-1;xn1=exp(-

40、n1/10).*(cos(w1/ws*n1)+cos(w2/ws*n1);%128点有效x(n)数据%在128点有效数据不补零情况下的分辨率演示xk11=fft(xn1,N1);mxk11=abs(xk11(1:N1/2);figure(1);subplot(211);plot(n1,xn1);xlabel('n');title('x(n) 0<=n<=127');axis(0,128,-3,3);k1=(0:N1/2-1)*fs/N1;subplot(212);plot(k1,mxk11);xlabel('频率 单位rad/s');

41、title('X1(k)的幅度谱');%在128点有效数据且补零至512点情况下分辨率演示xn2=xn1,zeros(1,N2-N1);xk12=fft(xn2,N2);mxk12=abs(xk12(1:N2/2);figure(2);subplot(211);plot(n2,xn2);xlabel('n');title('x(n) 0<=n<=511');axis(0,512,-3,3);k2=(0:N2/2-1)*fs/N2;subplot(212);plot(k2,mxk12);xlabel('频率 单位Hz')

42、;title('X1(k)补零后的幅度谱');%在512点有效数据下分辨率演示xn3=exp(-n2/10).*(cos(w1/ws*n2)+cos(w2/ws*n2);%512点有效x(n)数据xk2=fft(xn3,N2);mxk3=abs(xk2(1:N2/2);figure(3);subplot(211);plot(n2,xn3);xlabel('n');title('x(n) 0<=n<=511');axis(0,512,-3,3);k3=(0:N2/2-1)*fs/N2;subplot(212);plot(k3,mxk3)

43、;xlabel('频率 单位rad/s');title('512点有效数据的幅度谱');运行结果如题2-51图：题2-51图 频谱图252 设模拟信号，以时间间隔进行均匀采样，假设从开始采样，共采样点。（1）求采样后序列的表达式和对应的数字频率。（2）在此采样下值是否对采样失真有影响？（3）对进行点DFT，说明取哪些值时，DFT的结果能精确地反映 的频谱。（4）若要求DFT的分辨率达到1，应该采样多长时间的数据？解： （1）采样后序列的表达式为其对应的数字频率。（2）因为采样频率因此保证在一个周期内抽样四点（三点以上），无论取何值，根据抽样定理，都可以由准确重建

44、。（3）对进行DFT，要DFT的结果能精确地反映的频谱，根据，所以当时，就可以保证DFT结果的精确。（4）因为分辨率为因此若要求DFT的分辨率达到1，应该采样多的数据。253 用微处理机对实数序列做谱分析，要求谱分辨率，信号最高频率为，试确定以下各参数：（1） 最小记录时间；（2） 最大取样间隔；（3） 最少采样点数；（4） 在频带宽度不变的情况下，将频率分辨率提高一倍的值。解： （1）已知 （2）（3）（4）频带宽度不变意味着采样间隔不变，应该使记录时间扩大一倍为0.04s实现频带分辨率提高1倍。254 以的采样率对最高频率为的带限信号采样，然后计算的个采样点的DFT，即，（1）对应的模拟频

45、率是多少？ 呢？（2）频谱采样点之间的间隔是多少？解： （1）采样率，离散频率与模拟频率的关系是：，或。点DFT是对DTFT在个频率点上的采样： 所以，对应的模拟频率为 ， 或 时，序号对应。对于要特别注意，因为具有周期性： 对应的频率为，。对应的模拟频率为 或 （2）频谱采样点之间的间隔为 第三章31 画出级联型网络结构。解：32 画出级联型网络结构。解：33 已知某三阶数字滤波器的系统函数为，试画出其并联型网络结构。解：将系统函数表达为实系数一阶，二阶子系统之和，即：由上式可以画出并联型结构如题3-3图所示：题3-3图34 已知一FIR滤波器的系统函数为，画出该FIR滤波器的线性相位结构。

46、解： 因为，所以由第二类线性相位结构画出该滤波器的线性相位结构，如题3-4图所示：题3-4图35 已知一个FIR系统的转移函数为：求用级联形式实现的结构流图并用MATLAB画出其零点分布及其频率响应曲线。解： 由转移函数可知，且偶对称，故为线性相位系统，共有5个零点，为5阶系统，因而必存在一个一阶系统，即为系统的零点。而最高阶的系数为+1，所以为其零点。中包含项。所以：。 为一四阶子系统，设，代入等式，两边相等求得，得出系统全部零点，如图3-5（b）所示。 系统流图如题3-5（a）图所示。题3-5（a）图MATLAB程序如下，结果如题3-5（b）图所示： b=1 1.25 -2.75 -2.75 1.25 1; a=1; figure(1) zplane(b,a); figure(2); OMEGA=-pi:pi/100:pi; H=freqz(b,a,OMEGA);subplot(2,1,1),plot(OM