2011年高考数学总复习 提能拔高限时训练：平面、空间直线（练习+详细解析）大纲人教版

1、提能拔高限时训练39 平面、空间直线一、选择题1.下列推理错误的是( )A.Al,A,Bl,BlB.A,A,B,B=ABC.A、B、C,A、B、C,且A、B、C不共线与重合D.l,AlA解析：A、B、C分别是公理1、2、3的符号表示,故选D.对于D,l有两种可能,l,l与相交;若交点为A,则Al且A.答案：D2.若a、b是两条异面直线,且分别在平面、内,若=l,则直线l必定( )A.分别与a、b相交 B.至少与a、b之一相交C.与a、b都不相交 D.至多与a、b之一相交解析:(反证法)如果选项B不对,则l与a、b都不相交,由于l与a、b共面,则la,同理,lb,从而ab,这与a、b是异面直线矛

2、盾.答案:B3.若3个平面将空间分成n部分,则n的值为( )A.4 B.4或6C.4或6或7 D.4或6或7或8解析：若3个平面平行,则将平面分成4部分;若3个平面交于一条直线,将空间分成6部分;若3个平面两两相交有三条交线,当交线互相平行时,将空间分成7部分,三条交线交于一点时,将空间分成8部分.答案：D4.若P是两条异面直线l、m外的任意一点,则( )A.过点P有且仅有一条直线与l、m都平行B.过点P有且仅有一条直线与l、m都垂直C.过点P有且仅有一条直线与l、m都相交D.过点P有且仅有一条直线与l、m都异面解析：对于A,若存在直线n,使则有lm,与l、m异面矛盾;对于C,过点P与m、l都

3、相交的直线不一定存在,反例如图;对于D,过点P与l、m都异面的直线不唯一.答案：B5.如图,正四棱柱ABCDA1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )A. B. C. D.解析：连结BC1,则A1B与BC1所成的角即为所求.在A1BC1中,设AB=a,则A1B=BC1=,A1C1=,cosA1BC1=.答案：D6.一个正方体纸盒展开后如图所示,在原正方体纸盒中有下列结论:ABEF;AB与CM成60°角;EF与MN是异面直线;MNCD.其中正确的是( )A. B. C. D.解析：将其还原成正方体,如图所示,ABEF,EF与MN是异面直线,ABC

4、M,MNCD.只有正确,故选D.答案：D7.正六棱柱ABCDEFA1B1C1D1E1F1的底面边长为1,侧棱长为,则这个棱柱的侧面对角线E1D与BC1所成的角是（ ）A.90° B.60° C.45° D.30°解析：连结E1F、DF,则由正六棱柱相关性质,得FE1BC1,在EFD中,EF=FD=1,FED=120°,FD=.在RtEFE1和RtEE1D中,易得E1F=ED=,E1FD是等边三角形.FE1D=60°.BC1与DE1所成的角为60°.答案：B8.正方体ABCDA1B1C1D1中,P、Q、R分别为AB、AD、B1

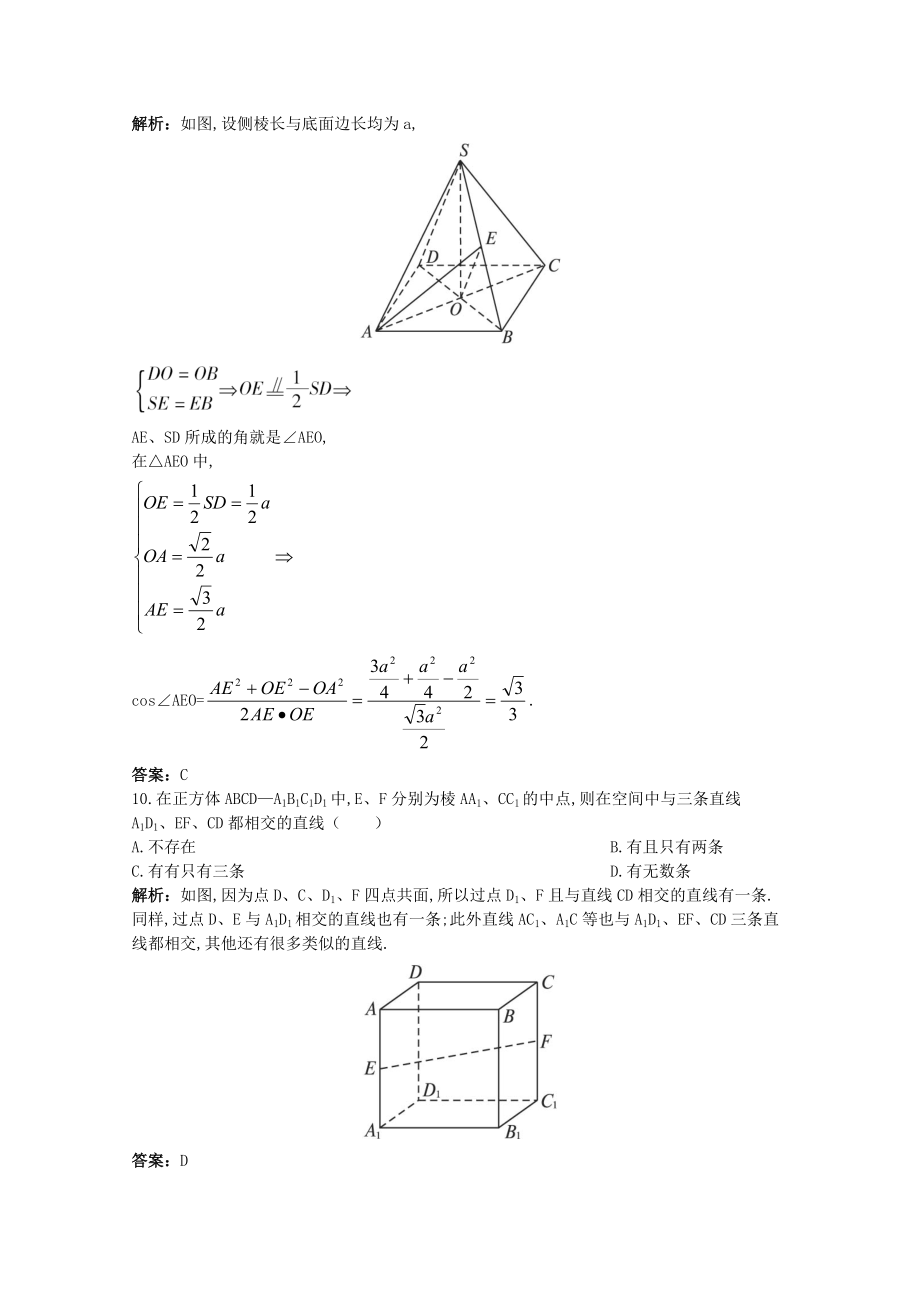
5、C1的中点,那么正方体过P、Q、R点的截面图形是( )A.三角形 B.四边形 C.五边形 D.六边形解析：设D1C1、D1D、BB1的中点分别为S、M、N,SRQP,S、R、Q、P四点共面,记为平面.QMSP,Q、M、S、P四点共面,记为平面.又、都经过点Q、P、S,与重合,即M.同理可证N.正方体过P、Q、R的截面为六边形.答案：D9.已知正四棱锥SABCD的侧棱长与底面边长都相等,E是SB的中点,则AE、SD所成的角的余弦值为（ ）A. B. C. D.解析：如图,设侧棱长与底面边长均为a,AE、SD所成的角就是AEO,在AEO中,cosAEO=.答案：C10.在正方体ABCDA1B1C1

6、D1中,E、F分别为棱AA1、CC1的中点,则在空间中与三条直线A1D1、EF、CD都相交的直线（ ）A.不存在 B.有且只有两条C.有有只有三条 D.有无数条解析：如图,因为点D、C、D1、F四点共面,所以过点D1、F且与直线CD相交的直线有一条.同样,过点D、E与A1D1相交的直线也有一条;此外直线AC1、A1C等也与A1D1、EF、CD三条直线都相交,其他还有很多类似的直线.答案：D二、填空题11.空间四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,(1)则四边形EFGH是_;(2)若ACBD,则四边形EFGH是_;(3)若AC=BD,则四边形EFGH是_;(4)若

7、四边形EFGH是正方形,则空间四边形中,必须有_;(5)若AC与BD成60°角,且AC=BD=a,则EG的长为_.解析：(1)E、F、G、H分别是边AB、BC、CD、DA的中点,EFAC且EF=AC,GHAC且GH=AC.EFGH且EF=GH.四边形EFGH是平行四边形.(2)若ACBD,则EFFG.四边形EFGH是矩形.(3)若AC=BD,则EF=FG.四边形EFGH是菱形.(4)若四边形EFGH是正方形,则它同时满足矩形和菱形的性质,空间四边形中,必须有ACBD且AC=BD.(5)由AC=BD=a,知EF=FG=.由AC与BD成60°角,EFG=60°或120

8、°.EG=或.答案：(1)平行四边形(2)矩形 (3)菱形(4)ACBD且AC=BD(5) 或12.如图,正方体ABCDA1B1C1D1中,M为BC的中点,则直线D1M与平面ABCD所成角的正切值为_,异面直线DC与D1M所成角的余弦值为_.解析:连结DM,DD1平面ABCD,D1MD即为D1M与平面ABCD所成的角.设正方体棱长为a,则DM=a,tanD1MD=,即D1M与平面ABCD所成的角的正切值为.连结MC1,DCD1C1,D1M与DC所成的角即为D1M与D1C1所成的角,即MD1C1.MC1=a,D1C1=a,D1M=a.cosC1D1M=即D1M与DC所成角的余弦值为.答

9、案: 13.等边三角形ABC与正方形ABDE有一公共边AB,二面角CABD的余弦值为,M、N分别是AC、BC的中点,则EM、AN所成角的余弦值等于_.解析：如图,设AB=a,则ABC的边长与正方形ABDE的边长都是a,取DE的中点F,分别连结MN、NF、CF、AF,因为M、N分别为AC、BC的中点,所以MNAB=EF.所以四边形MNFE为平行四边形.所以FNEM.所以ANF是AN与EM所成的角.因为AN=a,在RtAEF中,AF=,取AB的中点G,连结GF、CG,则CGAB,GFAB,所以CGF是二面角CABD的平面角,cosCGF=.又CG=a,GF=a,所以CF2=CG2+GF2-2CG&

10、#183;GF·=a2.所以CF=a.由图形的对称性,可知CE=CD,所以CFDE.所以CE2=CF2+EF2=a2.所以CE=AE=a.所以EMAC.又AM=a,所以EM=a=FN.在ANF中,cosANF=.答案：三、解答题14.已知正方体ABCDA1B1C1D1中，E、F分别为D1C1、C1B1的中点,ACBD=P,A1C1EF=Q.求证:(1)D、B、F、E四点共面;(2)若A1C交平面DBFE于R点,则P、Q、R三点共线.证明：如右图:(1)EF是D1B1C1的中位线,EFB1D1.在正方体AC1中,B1D1BD,EFBD,EF、BD确定一个平面,即D、B、F、E四点共面.

11、(2)正方体AC1中,设A1ACC1确定的平面为,平面BDEF为.QA1C1,Q.又QEF,Q.则Q点是与的公共点,同理,P点也是与的公共点,=PQ.又A1C=R,RA1C.R且R,则RPQ.故P、Q、R三点共线.15.如右图,已知矩形ABCD,PA平面ABCD,点M和N分别是线段AB和PC的中点.(1)证明MNCD;(2)若MN是异面直线PC与AB的公垂线,求异面直线MN与BC所成角的大小.(1)证明:设AC与BD交于点O,连结NO.N是PC的中点,O是AC的中点,NOPA.又PA平面AC,NO平面AC.MN在平面ABCD内的射影是MO.又MOCD,由三垂线定理,知MNCD.(2)解：由MO

12、BC,知NMO即为MN与BC所成的角.NM是PC与AB的公垂线,MNPC.又PN=NC,MP=MC.PA2=PM2-MA2=CM2-MB2=BC2,即PA=BC.NO=PA=BC.在RtMON中,tanNMO=1.NMO=45°,即MN与BC所成的角为45°.教学参考例题 志鸿优化系列丛书【例1】 正四面体PABC中,M为棱AB的中点,则PA与CM所成角的余弦值为（ ）A. B. C. D. 解析:方法一:取PB的中点E,连结CE、EM,则EMC为PA与CM所成的角,令正四面体的棱长为2,则CM=CE=,EM=1,cosEMC=.方法二:(坐标法)如图,建立空间直角坐标系,

13、设正方体的棱长为2,则A(2,0,0),B(0,2,0),P(2,2,2),C(0,0,2),M(1,1,0), =(1,1,-2), =(0,-2,-2),cos,=.答案：B【例2】 正方体ABCDABCD中,棱长为1,E、F分别是BC、CD上的点,且BE=CF=a(0a1),则DE与BF的位置关系是（ ）A.平行 B.垂直 C.相交 D.与a值有关解析:方法一:如图,连结AB,AB,AF,DE易知AB是DE在平面ABBA上的射影.ABAB,DEAB.又由BE=CF,知EC=FD,而AD=CD,RtDCERtADF.EDC=FAD.而EDC+EDA=90°,FAD+EDA=90&

14、#176;.从而AFDE.又易知DE是DE在底面ABCD上的射影,DEAF.综上,知DE平面ABF,从而DEBF.方法二:建立如图所示的空间直角坐标系,则D(0,0,1),E(1-a,1,0),B(1,1,1),F(0,1-a,0),=(1-a,1,-1), =(-1,-a,-1).=(1-a)×(-1)+1×(-a)+(-1)×(-1)=a-1-a+1=0.,即DEBF.答案：B【例3】 如图,直三棱柱ABCA1B1C1的侧棱长为2,底面ABC是等腰直角三角形,ACB=90°,AC=2,D、E分别是AA1、AB的中点.(1)求异面直线A1B1和C1D所成的角;(2)求证:A1EC1D.(1)解：取CC1的中点F,连结AF,则AFC1D.又A1B1AB,所以BAF为异面直线A1B1和C1D所成的角.又AC=2,AA1=2,AB=,AF=,在RtAEF中,又cosBAF=,所以BAF=arccos