2024年山东省高中自主招生数学模拟试卷试题（含答案）

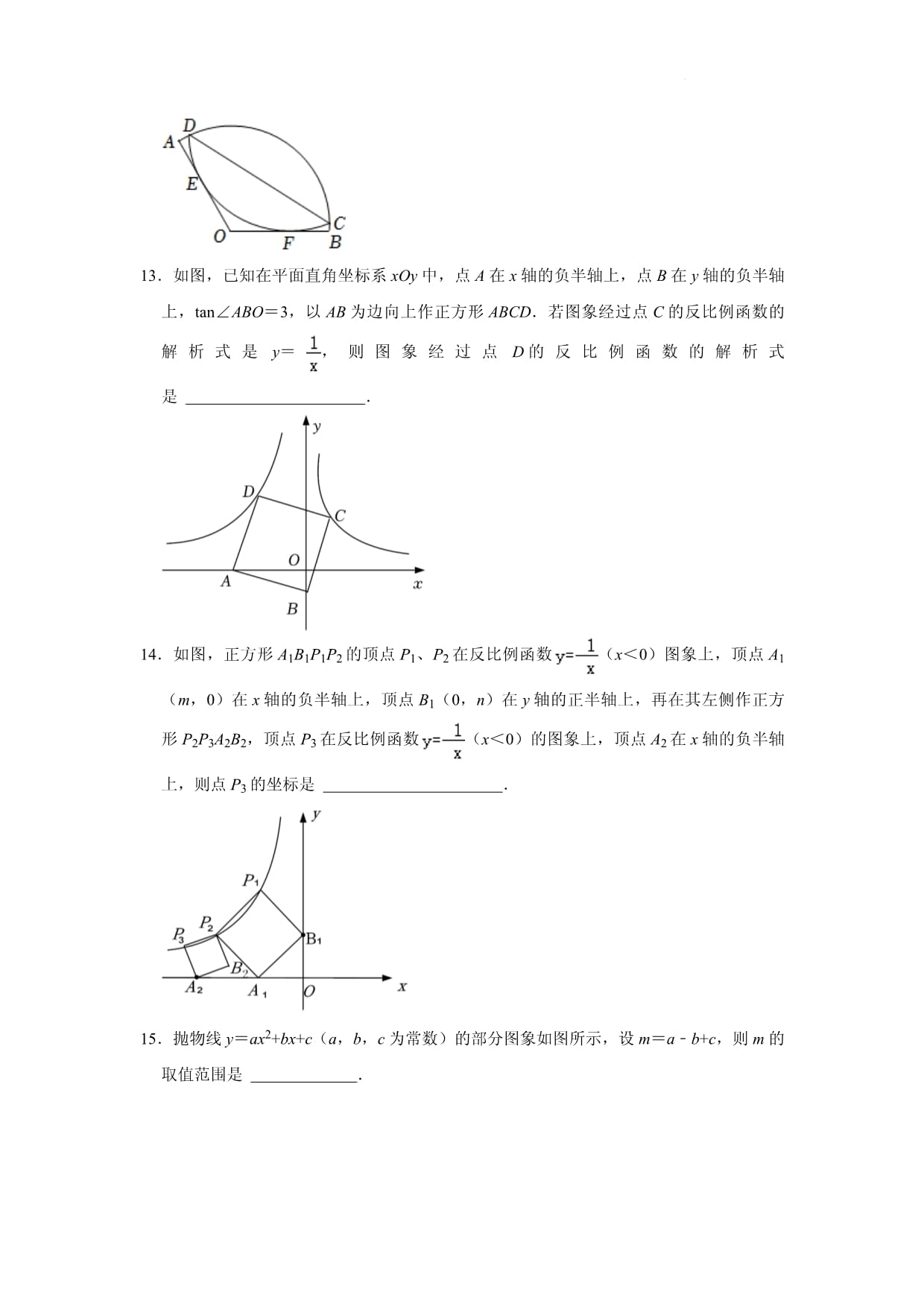
2024年山东省高中自主招生数学模拟试卷一、选择题1．若关于x的方程＝无解，则m的值为（）A．0 B．4或6 C．6 D．0或42．如图，圆锥底面圆半径为7cm，高为24cm，则它侧面展开图的面积是（）A．cm2 B．cm2 C．175πcm2 D．350πcm23．已知点A（a，b），B（4，c）在直线y＝kx+3（k为常数，k≠0）上，若ab的最大值为9，则c的值为（）A． B．2 C． D．14．已知二次函数y＝mx2﹣4m2x﹣3（m为常数，m≠0），点P（xp，yp）是该函数图象上一点，当0≤xp≤4时，yp≤﹣3，则m的取值范围是（）A．m≥1或m＜0 B．m≥1 C．m≤﹣1或m＞0 D．m≤﹣15．将抛物线y＝﹣（x﹣1）2位于直线y＝﹣1以下的图象沿直线y＝﹣1向上翻折所得的图象与不翻折的部分组成新图象，若新图象与直线y＝﹣x+a的交点少于4个，则a的取值范围是（）A．a≤1或 B． C． D．a≤1或6．如图，在Rt△ABC和Rt△BDE中，∠ABC＝∠BDE＝90°，点A在边DE的中点上，若AB＝BC，DB＝DE＝2，连结CE，则CE的长为（）A． B． C．4 D．7．如图是一张矩形纸片ABCD，点E为AD中点，点F在BC上，把该纸片沿EF折叠，点A，B的对应点分别为A′，B′，A′E与BC相交于点G，B′A′的延长线过点C．若＝，则的值为（）A．2 B． C． D．8．如图，正方形ABCD与正方形BEFG有公共顶点B，连接EC、GA，交于点O，GA与BC交于点P，连接OD、OB，则下列结论一定正确的是（）①EC⊥AG；②△OBP∽△CAP；③OB平分∠CBG；④∠AOD＝45°；A．①③ B．①②③ C．②③ D．①②④9．如图，在Rt△ABC中，∠ACB＝90°，以其三边为边向外作正方形，连结CF，作GM⊥CF于点M，BJ⊥GM于点J，AK⊥BJ于点K，交CF于点L．若正方形ABGF与正方形JKLM的面积之比为5，CE＝+，则CH的长为（）A． B． C．2 D．10．如图，正方形ABCD的顶点分别在反比例函数y＝（k1＞0）和y＝（k2＞0）的图象上．若BD∥y轴，点D的横坐标为3，则k1+k2＝（）A．36 B．18 C．12 D．9二、填空题11．如图，矩形ABCD中，AB＝6，AD＝4，点E、F分别是AB、DC上的动点，EF∥BC，则AF+CE的最小值是．12．如图，在扇形AOB中，点C，D在上，将沿弦CD折叠后恰好与OA，OB相切于点E，F．已知∠AOB＝120°，OA＝6，则的度数为，折痕CD的长为．13．如图，已知在平面直角坐标系xOy中，点A在x轴的负半轴上，点B在y轴的负半轴上，tan∠ABO＝3，以AB为边向上作正方形ABCD．若图象经过点C的反比例函数的解析式是y＝，则图象经过点D的反比例函数的解析式是．14．如图，正方形A1B1P1P2的顶点P1、P2在反比例函数（x＜0）图象上，顶点A1（m，0）在x轴的负半轴上，顶点B1（0，n）在y轴的正半轴上，再在其左侧作正方形P2P3A2B2，顶点P3在反比例函数（x＜0）的图象上，顶点A2在x轴的负半轴上，则点P3的坐标是．15．抛物线y＝ax2+bx+c（a，b，c为常数）的部分图象如图所示，设m＝a﹣b+c，则m的取值范围是．16．如图，在四边形ABCD中，∠A＝∠ABC＝90°，DB平分∠ADC．若AD＝1，CD＝3，则sin∠ABD＝．17．如图，在菱形ABCD中，过点D作DE⊥CD交对角线AC于点E，连接BE，点P是线段BE上一动点，作P关于直线DE的对称点P'，点Q是AC上一动点，连接P'Q，DQ．若AE＝14，CE＝18，则DQ﹣P'Q的最大值为．三、解答题18．如图所示，九（1）班数学兴趣小组为了测量河对岸的古树A、B之间的距离，他们在河边与AB平行的直线l上取相距60m的C、D两点，测得∠ACB＝15°，∠BCD＝120°，∠ADC＝30°．（1）求河的宽度；（2）求古树A、B之间的距离．（结果保留根号）19．如图，在Rt△ABC中，∠B＝90°，AE平分∠BAC交BC于点E，O为AC上一点，经过点A、E的⊙O分别交AB、AC于点D、F，连接OD交AE于点M．（1）求证：BC是⊙O的切线．（2）若CF＝2，sinC＝，求AE的长．20．如图，在平面直角坐标系xOy中，一次函数y＝﹣2x+6的图象与反比例函数y＝的图象相交于A（a，4），B两点．（1）求反比例函数的表达式及点B的坐标；（2）过点A作直线AC，交反比例函数图象于另一点C，连接BC，当线段AC被y轴分成长度比为1：2的两部分时，求BC的长；（3）我们把有两个内角是直角，且一条对角线垂直平分另一条对角线的四边形称为“完美筝形”．设P是第三象限内的反比例函数图象上一点，Q是平面内一点，当四边形ABPQ是完美筝形时，求P，Q两点的坐标．21．如图，在矩形ABCD中，点O是AB的中点，点M是射线DC上动点，点P在线段AM上（不与点A重合），OP＝AB．（1）判断△ABP的形状，并说明理由．（2）当点M为边DC中点时，连接CP并延长交AD于点N．求证：PN＝AN．（3）点Q在边AD上，AB＝5，AD＝4，DQ＝，当∠CPQ＝90°时，求DM的长．22．如图，△ABC和△DBE的顶点B重合，∠ABC＝∠DBE＝90°，∠BAC＝∠BDE＝30°，BC＝3，BE＝2．（1）特例发现：如图1，当点D，E分别在AB，BC上时，可以得出结论：＝，直线AD与直线CE的位置关系是；（2）探究证明：如图2，将图1中的△DBE绕点B顺时针旋转，使点D恰好落在线段AC上，连接EC，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由；（3）拓展运用：如图3，将图1中的△DBE绕点B顺时针旋转α（19°＜α＜60°），连接AD、EC，它们的延长线交于点F，当DF＝BE时，求tan（60°﹣α）的值．23．如图（1），二次函数y＝﹣x2+bx+c的图象与x轴交于A、B两点，与y轴交于C点，点B的坐标为（3，0），点C的坐标为（0，3），直线l经过B、C两点．（1）求该二次函数的表达式及其图象的顶点坐标；（2）点P为直线l上的一点，过点P作x轴的垂线与该二次函数的图象相交于点M，再过点M作y轴的垂线与该二次函数的图象相交于另一点N，当PM＝MN时，求点P的横坐标；（3）如图（2），点C关于x轴的对称点为点D，点P为线段BC上的一个动点，连接AP，点Q为线段AP上一点，且AQ＝3PQ，连接DQ，当3AP+4DQ的值最小时，直接写出DQ的长．

参考答案与试题解析一、选择题1．若关于x的方程＝无解，则m的值为（）A．0 B．4或6 C．6 D．0或4【解答】解：＝，2（2x+1）＝mx，4x+2＝mx，（4﹣m）x＝﹣2，∵方程无解，∴4﹣m＝0或2x+1＝0或x＝0，即4﹣m＝0或x＝﹣＝﹣，∴m＝4或m＝0，故选：D．2．如图，圆锥底面圆半径为7cm，高为24cm，则它侧面展开图的面积是（）A．cm2 B．cm2 C．175πcm2 D．350πcm2【解答】解：在Rt△AOC中，AC＝＝25（cm），所以圆锥的侧面展开图的面积＝×2π×7×25＝175π（cm2）．故选：C．3．已知点A（a，b），B（4，c）在直线y＝kx+3（k为常数，k≠0）上，若ab的最大值为9，则c的值为（）A． B．2 C． D．1【解答】解：∵点A（a，b），B（4，c）在直线y＝kx+3上，∴，由①可得：ab＝a（ak+3）＝ka2+3a＝k（a+）2﹣，∵ab的最大值为9，∴k＜0，﹣＝9，解得k＝﹣，把k＝﹣代入②得：4×（﹣）+3＝c，∴c＝2，故选：B．4．已知二次函数y＝mx2﹣4m2x﹣3（m为常数，m≠0），点P（xp，yp）是该函数图象上一点，当0≤xp≤4时，yp≤﹣3，则m的取值范围是（）A．m≥1或m＜0 B．m≥1 C．m≤﹣1或m＞0 D．m≤﹣1【解答】解：∵二次函数y＝mx2﹣4m2x﹣3，∴对称轴为x＝2m，抛物线与y轴的交点为（0，﹣3），∵点P（xp，yp）是该函数图象上一点，当0≤xp≤4时，yp≤﹣3，∴①当m＞0时，对称轴x＝2m＞0，此时，当x＝4时，y≤﹣3，即m•42﹣4m2•4﹣3≤﹣3，解得m≥1；②当m＜0时，对称轴x＝2m＜0，当0≤x≤4时，y随x增大而减小，则当0≤xp≤4时，yp≤﹣3恒成立；综上，m的取值范围是：m≥1或m＜0．故选：A．5．将抛物线y＝﹣（x﹣1）2位于直线y＝﹣1以下的图象沿直线y＝﹣1向上翻折所得的图象与不翻折的部分组成新图象，若新图象与直线y＝﹣x+a的交点少于4个，则a的取值范围是（）A．a≤1或 B． C． D．a≤1或【解答】解：如图：在y＝﹣（x﹣1）2中，令y＝﹣1得x＝2或x＝0，∴B（2，﹣1），由图可知，当直线y＝﹣x+a经过B时，新图象与直线y＝﹣x+a的交点有3个，此时﹣1＝﹣2+a，∴a＝1，当直线y＝﹣x+a为直线l2时，新图象与直线y＝﹣x+a的交点有3个，此时﹣（x﹣1）2＝﹣x+a有两个相等实数根，即x2﹣3x+a+1＝0的判别式Δ＝0，∴9﹣4（a+1）＝0，∴a＝，由图可知，若新图象与直线y＝﹣x+a的交点少于4个，则a≤1或a≥，故选：D．6．如图，在Rt△ABC和Rt△BDE中，∠ABC＝∠BDE＝90°，点A在边DE的中点上，若AB＝BC，DB＝DE＝2，连结CE，则CE的长为（）A． B． C．4 D．【解答】解：方法一：作EF⊥CB交CB的延长线于点F，作EG⊥BA交BA的延长线于点G，∵DB＝DE＝2，∠BDE＝90°，点A是DE的中点，∴BE＝＝＝2，DA＝EA＝1，∴AB＝＝＝，∵AB＝BC，∴BC＝，∵＝，∴，解得EG＝，∵EG⊥BG，EF⊥BF，∠ABF＝90°，∴四边形EFBG是矩形，∴EG＝BF＝，∵BE＝2，BF＝，∴EF＝＝＝，CF＝BF+BC＝+＝，∵∠EFC＝90°，∴EC＝＝＝，故选：D．方法二：延长ED到F，使得DE＝DF，连接CF，BF，如图所示，∵BD＝DE＝2，∠BDE＝90°，∴∠BDE＝∠BDF＝90°，EF＝4，∴△BDE≌△BDF（SAS），∴BE＝BF，∠BEA＝∠BFA＝45°，∵∠EBA+∠ABF＝90°，∠ABF+∠FBC＝90°，∴∠EBA＝∠FBC，∵BE＝BF，BA＝BC，∴△EBA≌△FBC（SAS），∴∠BEA＝∠BFC＝45°，AE＝CF，∴∠CFE＝∠BFC+∠AFB＝90°，∵点A为DE的中点，∴AE＝1，∴CF＝1，∴EC＝＝＝，故选：D．7．如图是一张矩形纸片ABCD，点E为AD中点，点F在BC上，把该纸片沿EF折叠，点A，B的对应点分别为A′，B′，A′E与BC相交于点G，B′A′的延长线过点C．若＝，则的值为（）A．2 B． C． D．【解答】解：连接FG，CA′，过点G作GT⊥AD于点T．设AB＝x，AD＝y．∵＝，∴可以假设BF＝2k，CG＝3k．∵AE＝DE＝y，由翻折的性质可知EA＝EA′＝y，BF＝FB′＝2k，∠AEF＝∠GEF，∵AD∥CB，∴∠AEF＝∠EFG，∴∠GEF＝∠GFE，∴EG＝FG＝y﹣5k，∴GA′＝y﹣（y﹣5k）＝5k﹣y，∵C，A′，B′共线，GA′∥FB′，∴＝，∴＝，∴y2﹣12ky+32k2＝0，∴y＝8k或y＝4k（舍去），∴AE＝DE＝4k，∵四边形CDTG是矩形，∴CG＝DT＝3k，∴ET＝k，∵EG＝8k﹣5k＝3k，∴AB＝CD＝GT＝＝2k，∴＝＝2．解法二：不妨设BF＝2，CG＝3，连接CE，则Rt△CA'E≌Rt△CDE，推出A'C＝CD＝AB＝A'B'，＝＝1，推出GF＝CG＝3，BC＝8，在Rt△CB'F，勾股得CB'＝4则A'B'＝2，故选：A．8．如图，正方形ABCD与正方形BEFG有公共顶点B，连接EC、GA，交于点O，GA与BC交于点P，连接OD、OB，则下列结论一定正确的是（）①EC⊥AG；②△OBP∽△CAP；③OB平分∠CBG；④∠AOD＝45°；A．①③ B．①②③ C．②③ D．①②④【解答】解：∵四边形ABCD、四边形BEFG是正方形，∴AB＝BC，BG＝BE，∠ABC＝90°＝∠GBE，∴∠ABC+∠CBG＝∠GBE+∠CBG，即∠ABG＝∠EBC，∴△ABG≌△CBE（SAS），∴∠BAG＝∠BCE，∵∠BAG+∠APB＝90°，∴∠BCE+∠APB＝90°，∴∠BCE+∠OPC＝90°，∴∠POC＝90°，∴EC⊥AG，故①正确；取AC的中点K，如图：在Rt△AOC中，K为斜边AC上的中点，∴AK＝CK＝OK，在Rt△ABC中，K为斜边AC上的中点，∴AK＝CK＝BK，∴AK＝CK＝OK＝BK，∴A、B、O、C四点共圆，∴∠BOA＝∠BCA，∵∠BPO＝∠CPA，∴△OBP∽△CAP，故②正确，∵∠AOC＝∠ADC＝90°，∴∠AOC+∠ADC＝180°，∴A、O、C、D四点共圆，∵AD＝CD，∴∠AOD＝∠DOC＝45°，故④正确，由已知不能证明OB平分∠CBG，故③错误，故正确的有：①②④，故选：D．9．如图，在Rt△ABC中，∠ACB＝90°，以其三边为边向外作正方形，连结CF，作GM⊥CF于点M，BJ⊥GM于点J，AK⊥BJ于点K，交CF于点L．若正方形ABGF与正方形JKLM的面积之比为5，CE＝+，则CH的长为（）A． B． C．2 D．【解答】解：设CF交AB于点P，过C作CN⊥AB于点N，如图：设正方形JKLM边长为m，∴正方形JKLM面积为m2，∵正方形ABGF与正方形JKLM的面积之比为5，∴正方形ABGF的面积为5m2，∴AF＝AB＝m，由已知可得：∠AFL＝90°﹣∠MFG＝∠MGF，∠ALF＝90°＝∠FMG，AF＝GF，∴△AFL≌△FGM（AAS），∴AL＝FM，设AL＝FM＝x，则FL＝FM+ML＝x+m，在Rt△AFL中，AL2+FL2＝AF2，∴x2+（x+m）2＝（m）2，解得x＝m或x＝﹣2m（舍去），∴AL＝FM＝m，FL＝2m，∵tan∠AFL＝＝＝＝，∴＝，∴AP＝，∴FP＝＝＝m，BP＝AB﹣AP＝m﹣＝，∴AP＝BP，即P为AB中点，∵∠ACB＝90°，∴CP＝AP＝BP＝，∵∠CPN＝∠APF，∠CNP＝90°＝∠FAP，∴△CPN∽△FPA，∴＝＝，即＝＝，∴CN＝m，PN＝m，∴AN＝AP+PN＝m，∴tan∠BAC＝＝＝＝，∵△AEC和△BCH是等腰直角三角形，∴△AEC∽△BCH，∴＝，∵CE＝+，∴＝，∴CH＝2，故选：C．10．如图，正方形ABCD的顶点分别在反比例函数y＝（k1＞0）和y＝（k2＞0）的图象上．若BD∥y轴，点D的横坐标为3，则k1+k2＝（）A．36 B．18 C．12 D．9【解答】解：连接AC交BD于E，延长BD交x轴于F，连接OD、OB，如图：∵四边形ABCD是正方形，∴AE＝BE＝CE＝DE，设AE＝BE＝CE＝DE＝m，D（3，a），∵BD∥y轴，∴B（3，a+2m），A（3+m，a+m），∵A，B都在反比例函数y＝（k1＞0）的图象上，∴k1＝3（a+2m）＝（3+m）（a+m），∵m≠0，∴m＝3﹣a，∴B（3，6﹣a），∵B（3，6﹣a）在反比例函数y＝（k1＞0）的图象上，D（3，a）在y＝（k2＞0）的图象上，∴k1＝3（6﹣a）＝18﹣3a，k2＝3a，∴k1+k2＝18﹣3a+3a＝18；故选：B．二、填空题11．如图，矩形ABCD中，AB＝6，AD＝4，点E、F分别是AB、DC上的动点，EF∥BC，则AF+CE的最小值是10．【解答】解：延长BC到G，使CG＝EF，连接FG，∵EF∥CG，EF＝CG，∴四边形EFGC是平行四边形，∴CE＝FG，∴AF+CE＝AF+FG，∴当点A、F、G三点共线时，AF+CE的值最小为AG，由勾股定理得，AG＝＝＝10，∴AF+CE的最小值为10，故答案为：10．12．如图，在扇形AOB中，点C，D在上，将沿弦CD折叠后恰好与OA，OB相切于点E，F．已知∠AOB＝120°，OA＝6，则的度数为60°，折痕CD的长为4．【解答】解：如图，设翻折后的弧的圆心为O′，连接O′E，O′F，OO′，O′C，OO′交CD于点H，∴OO′⊥CD，CH＝DH，O′C＝OA＝6，∵将沿弦CD折叠后恰好与OA，OB相切于点E，F．∴∠O′EO＝∠O′FO＝90°，∵∠AOB＝120°，∴∠EO′F＝60°，则的度数为60°；∵∠AOB＝120°，∴∠O′OF＝60°，∵O′F⊥OB，O′E＝O′F＝O′C＝6，∴OO′＝＝＝4，∴O′H＝2，∴CH＝＝＝2，∴CD＝2CH＝4．故答案为：60°，4．13．如图，已知在平面直角坐标系xOy中，点A在x轴的负半轴上，点B在y轴的负半轴上，tan∠ABO＝3，以AB为边向上作正方形ABCD．若图象经过点C的反比例函数的解析式是y＝，则图象经过点D的反比例函数的解析式是y＝﹣．【解答】解：如图，过点C作CT⊥y轴于点T，过点D作DH⊥CT交CT的延长线于点H．∵tan∠ABO＝＝3，∴可以假设OB＝a，OA＝3a，∵四边形ABCD是正方形，∴AB＝BC，∠ABC＝∠AOB＝∠BTC＝90°，∴∠ABO+∠CBT＝90°，∠CBT+∠BCT＝90°，∴∠ABO＝∠BCT，∴△AOB≌△BTC（AAS），∴BT＝OA＝3a，OB＝TC＝a，∴OT＝BT﹣OB＝2a，∴C（a，2a），∵点C在y＝的图象上，∴2a2＝1，同法可证△CHD≌△BTC，∴DH＝CT＝a，CH＝BT＝3a，∴D（﹣2a，3a），设经过点D的反比例函数的解析式为y＝，则有﹣2a×3a＝k，∴k＝﹣6a2＝﹣3，∴经过点D的反比例函数的解析式是y＝﹣．故答案为：y＝﹣．14．如图，正方形A1B1P1P2的顶点P1、P2在反比例函数（x＜0）图象上，顶点A1（m，0）在x轴的负半轴上，顶点B1（0，n）在y轴的正半轴上，再在其左侧作正方形P2P3A2B2，顶点P3在反比例函数（x＜0）的图象上，顶点A2在x轴的负半轴上，则点P3的坐标是（﹣，﹣）．【解答】解：作P1C⊥y轴于C，P2D⊥x轴于D，P3E⊥x轴于E，P3F⊥P2D于F，如图所示：∵四边形A1B1P1P2为正方形，∴∠A1B1P1＝90°，∴∠CB1P1+∠OB1A1＝90°，∵∠CB1P1+∠CP1B1＝90°，∠OB1A1+∠OA1B1＝90°，∴∠CB1P1＝∠OA1B1，在△P1B1C和△B1A1O中，，∴△P1B1C≌△B1A1O（AAS），同理：△B1A1O≌△A1P2D，∴OB1＝P1C＝A1D＝n，∴OA1＝B1C＝P2D，∴P1（﹣n，），∴OA1＝B1C＝P2D＝﹣n，∴OD＝﹣n+n＝，∴P2的坐标为（﹣，﹣n），把P2的坐标代入y＝（x＜0）得：﹣•（﹣n）＝﹣1，解得：n＝﹣（舍去）或n＝，∴P2（﹣，），设P3的坐标为（﹣，b），又∵四边形P2P3A2B2为正方形，同上：△P2P3F≌△A2P3E，∴P3E＝P3F＝DE＝b，∴OE＝OD+DE＝+b，∴+b＝，解得：b＝（舍去），b＝，∴﹣＝﹣，∴点P3的坐标为（﹣，﹣）．故答案为：（﹣，﹣）．15．抛物线y＝ax2+bx+c（a，b，c为常数）的部分图象如图所示，设m＝a﹣b+c，则m的取值范围是﹣4＜m＜0．【解答】解：∵抛物线开口向上，∴a＞0，∵抛物线对称轴在y轴左侧，∴﹣＜0，∴b＞0，∵抛物线经过（0，﹣2），∴c＝﹣2，∵抛物线经过（1，0），∴a+b+c＝0，∴a+b＝2，b＝2﹣a，∴m＝a﹣b+c＝a﹣（2﹣a）+（﹣2）＝2a﹣4，∴y＝ax2+（2﹣a）x﹣2，当x＝﹣1时，y＝a+a﹣2﹣2＝2a﹣4，∵b＝2﹣a＞0，∴0＜a＜2，∴﹣4＜2a﹣4＜0，故答案为：﹣4＜m＜0．16．如图，在四边形ABCD中，∠A＝∠ABC＝90°，DB平分∠ADC．若AD＝1，CD＝3，则sin∠ABD＝．【解答】解：过点D作DE⊥BC，垂足为E，如图，∵∠A＝∠ABC＝90°，∴AD∥BC，∴∠ADB＝∠CBD，∵DB平分∠ADC，∴∠ADB＝∠CDB，∴CD＝CB＝3，∵AD＝BE＝1，∴CE＝BC﹣BE＝3﹣1＝2，在Rt△CDE中，DE＝＝＝，∵DE＝AB，在Rt△ADB中，＝＝，∴sin∠ABD＝＝．故答案为：．17．如图，在菱形ABCD中，过点D作DE⊥CD交对角线AC于点E，连接BE，点P是线段BE上一动点，作P关于直线DE的对称点P'，点Q是AC上一动点，连接P'Q，DQ．若AE＝14，CE＝18，则DQ﹣P'Q的最大值为．【解答】解：如图，连接BD交AC于点O，过点D作DK⊥BC于点K，延长DE交AB于点R，连接EP′并延长，延长线交AB于点J，作EJ关于AC的对称线段EJ′，则点P′的对应点P″在线段EJ′上．当点P是定点时，DQ﹣QP′＝DQ﹣QP″，当D，P″，Q共线时，QD﹣QP′的值最大，最大值是线段DP″的长，当点P与B重合时，点P″与J′重合，此时DQ﹣QP′的值最大，最大值是线段DJ′的长，也就是线段BJ的长．∵四边形ABCD是菱形，∴AC⊥BD，AO＝OC，∵AE＝14．EC＝18，∴AC＝32，AO＝OC＝16，∴OE＝AO﹣AE＝16﹣14＝2，∵DE⊥CD，∴∠DOE＝∠EDC＝90°，∵∠DEO＝∠DEC，∴△EDO∽△ECD，∴DE2＝EO•EC＝36，∴DE＝EB＝EJ＝6，∴CD＝＝＝12，∴OD＝＝＝4，∴BD＝8，∵S△DCB＝×OC×BD＝BC•DK，∴DK＝＝，∵∠BER＝∠DCK，∴sin∠BER＝sin∠DCK＝＝＝，∴RB＝BE×＝，∵EJ＝EB，ER⊥BJ，∴JR＝BR＝，∴JB＝DJ′＝，∴DQ﹣P'Q的最大值为．解法二：DQ﹣P'Q＝BQ﹣P'Q≤BP'，显然P'的轨迹EJ，故最大值为BJ．勾股得CD，OD．△BDJ∽△BAD，BD2＝BJ*BA，可得BJ＝．故答案为：．三、解答题18．如图所示，九（1）班数学兴趣小组为了测量河对岸的古树A、B之间的距离，他们在河边与AB平行的直线l上取相距60m的C、D两点，测得∠ACB＝15°，∠BCD＝120°，∠ADC＝30°．（1）求河的宽度；（2）求古树A、B之间的距离．（结果保留根号）【解答】解：（1）过点A作AE⊥l，垂足为E，设CE＝x米，∵CD＝60米，∴DE＝CE+CD＝（x+60）米，∵∠ACB＝15°，∠BCD＝120°，∴∠ACE＝180°﹣∠ACB﹣∠BCD＝45°，在Rt△AEC中，AE＝CE•tan45°＝x（米），在Rt△ADE中，∠ADE＝30°，∴tan30°＝＝＝，∴x＝30+30，经检验：x＝30+30是原方程的根，∴AE＝（30+30）米，∴河的宽度为（30+30）米；（2）过点B作BF⊥l，垂足为F，则CE＝AE＝BF＝（30+30）米，AB＝EF，∵∠BCD＝120°，∴∠BCF＝180°﹣∠BCD＝60°，在Rt△BCF中，CF＝＝＝（30+10）米，∴AB＝EF＝CE﹣CF＝30+30﹣（30+10）＝20（米），∴古树A、B之间的距离为20米．19．如图，在Rt△ABC中，∠B＝90°，AE平分∠BAC交BC于点E，O为AC上一点，经过点A、E的⊙O分别交AB、AC于点D、F，连接OD交AE于点M．（1）求证：BC是⊙O的切线．（2）若CF＝2，sinC＝，求AE的长．【解答】（1）证明：连接OE，方法一：∵AE平分∠BAC交BC于点E，∴∠BAC＝2∠OAE，∵∠FOE＝2∠OAE，∴∠FOE＝∠BAC，∴OE∥AB，∵∠B＝90°，∴OE⊥BC，又∵OE是⊙O的半径，∴BC是⊙O的切线；方法二：∵AE平分∠BAC交BC于点E，∴∠OAE＝∠BAE，∵OA＝OE，∴∠OAE＝∠OEA，∴∠BAE＝∠OEA，∴OE∥AB，∵∠B＝90°，∴OE⊥BC，又∵OE是⊙O的半径，∴BC是⊙O的切线；（2）解：连接EF，∵CF＝2，sinC＝，∴，∵OE＝OF，∴OE＝OF＝3，∵OA＝OF＝3，∴AC＝OA+OF+CF＝8，∴AB＝AC•sinC＝8×＝，∵∠OAE＝∠BAE，∴cos∠OAE＝cos∠BAE，即，∴，解得AE＝（舍去负数），∴AE的长为．20．如图，在平面直角坐标系xOy中，一次函数y＝﹣2x+6的图象与反比例函数y＝的图象相交于A（a，4），B两点．（1）求反比例函数的表达式及点B的坐标；（2）过点A作直线AC，交反比例函数图象于另一点C，连接BC，当线段AC被y轴分成长度比为1：2的两部分时，求BC的长；（3）我们把有两个内角是直角，且一条对角线垂直平分另一条对角线的四边形称为“完美筝形”．设P是第三象限内的反比例函数图象上一点，Q是平面内一点，当四边形ABPQ是完美筝形时，求P，Q两点的坐标．【解答】解：（1）∵一次函数y＝﹣2x+6的图象过点A，∴4＝﹣2a+6，∴a＝1，∴点A（1，4），∵反比例函数y＝的图象过点A（1，4），∴k＝1×4＝4；∴反比例函数的解析式为：y＝，联立方程组可得：，解得：，，∴点B（2，2）；（2）如图，过点A作AE⊥y轴于E，过点C作CF⊥y轴于F，∴AE∥CF，∴△AEH∽△CFH，∴，当＝时，则CF＝2AE＝2，∴点C（﹣2，﹣2），∴BC＝＝4，当＝2时，则CF＝AE＝，∴点C（﹣，﹣8），∴BC＝＝，综上所述：BC的长为4或；（3）如图，当∠AQP＝∠ABP＝90°时，设直线AB与y轴交于点E，过点B作BF⊥y轴于F，设BP与y轴的交点为N，连接BQ，AP交于点H，∵直线y＝﹣2x+6与y轴交于点E，∴点E（0，6），∵点B（2，2），∴BF＝OF＝2，∴EF＝4，∵∠ABP＝90°，∴∠ABF+∠FBN＝90°＝∠ABF+∠BEF，∴∠BEF＝∠FBN，又∵∠EFB＝∠BFN＝90°，∴△EBF∽△BNF，∴，∴FN＝＝1，∴点N（0，1），∴直线BN的解析式为：y＝x+1，联立方程组得：，解得：，，∴点P（﹣4，﹣1），∴直线AP的解析式为：y＝x+3，∵AP垂直平分BQ，∴设BQ的解析式为y＝﹣x+4，∴x+3＝﹣x+4，∴x＝，∴点H（，），∵点H是BQ的中点，点B（2，2），∴点Q（﹣1，5）．21．如图，在矩形ABCD中，点O是AB的中点，点M是射线DC上动点，点P在线段AM上（不与点A重合），OP＝AB．（1）判断△ABP的形状，并说明理由．（2）当点M为边DC中点时，连接CP并延长交AD于点N．求证：PN＝AN．（3）点Q在边AD上，AB＝5，AD＝4，DQ＝，当∠CPQ＝90°时，求DM的长．【解答】（1）解：△ABP是直角三角形，理由如下：∵点O是AB的中点，∴AO＝OB＝AB，∵OP＝AB，∴OP＝OA＝OB，∴∠OBP＝∠OPB，∠OAP＝∠APO，∵∠OAP+∠APO+∠OBP+∠BPO＝180°，∴∠APO+∠BPO＝90°，∴∠APB＝90°，∴△ABP是直角三角形；（2）证明：如图1，延长AM，BC交于点Q，∵M是CD的中点，∴DM＝CM，∵∠D＝∠MCQ＝90°，∠AMD＝∠QMC，∴△ADM≌△QCM（ASA），∴AD＝CQ＝BC，∵∠BPQ＝90°，∴PC＝BQ＝BC，∴∠CPB＝∠CBP，∵∠OPB＝∠OBP，∴∠OBC＝∠OPC＝90°，∴∠OPN＝∠OPA+∠APN＝90°，∵∠OAP+∠PAN＝90°，∠OAP＝∠OPA，∴∠APN＝∠PAN，∴PN＝AN；（3）解：分两种情况：①如图2，点M在CD上时，过点P作GH∥CD，交AD于G，交BC于H，设DM＝x，QG＝a，则CH＝a+，BH＝AG＝4﹣﹣a＝﹣a，∵PG∥DM，∴△AGP∽△ADM，∴＝，即，∴PG＝x﹣ax，∵∠CPQ＝90°，∴∠CPH+∠QPG＝90°，∵∠CPH+∠PCH＝90°，∴∠QPG＝∠PCH，∴tan∠QPG＝tan∠PCH，即＝，∴PH•PG＝QG•CH，同理得：∠APG＝∠PBH，∴tan∠APG＝tan∠PBH，即＝，∴PG•PH＝AG•BH＝AG2，∴AG2＝QG•CH，即（﹣a）2＝a（+a），∴a＝，∵PG•PH＝AG2，∴（x﹣x）•（5﹣x+x）＝（﹣）2，解得：x1＝12（舍），x2＝，∴DM＝；②如图3，当M在DC的延长线上时，同理得：DM＝12，综上，DM的长是或12．22．如图，△ABC和△DBE的顶点B重合，∠ABC＝∠DBE＝90°，∠BAC＝∠BDE＝30°，BC＝3，BE＝2．（1）特例发现：如图1，当点D，E分别在AB，BC上时，可以得出结论：＝，直线AD与直线CE的位置关系是垂直；（2）探究证明：如图2，将图1中的△DBE绕点B顺时针旋转，使点D恰好落在线段AC上，连接EC，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由；（3）拓展运用：如图3，将图1中的△DBE绕点B顺时针旋转α（19°＜α＜60°），连接AD、EC，它们的延长线交于点F，当DF＝BE时，求tan（60°﹣α）的值．【解答】解：（1）在Rt△ABC中，∠B＝90°，BC＝3，∠A＝30°，∴AB＝BC＝3，在Rt△BDE中，∠BDE＝30°，BE＝2，∴BD＝BE＝2，∴EC＝1，AD＝，∴＝，此时AD⊥EC，故答案为：，垂直；（2）结论成立．理