组合第一课时市公开课一等奖省赛课微课金奖课件

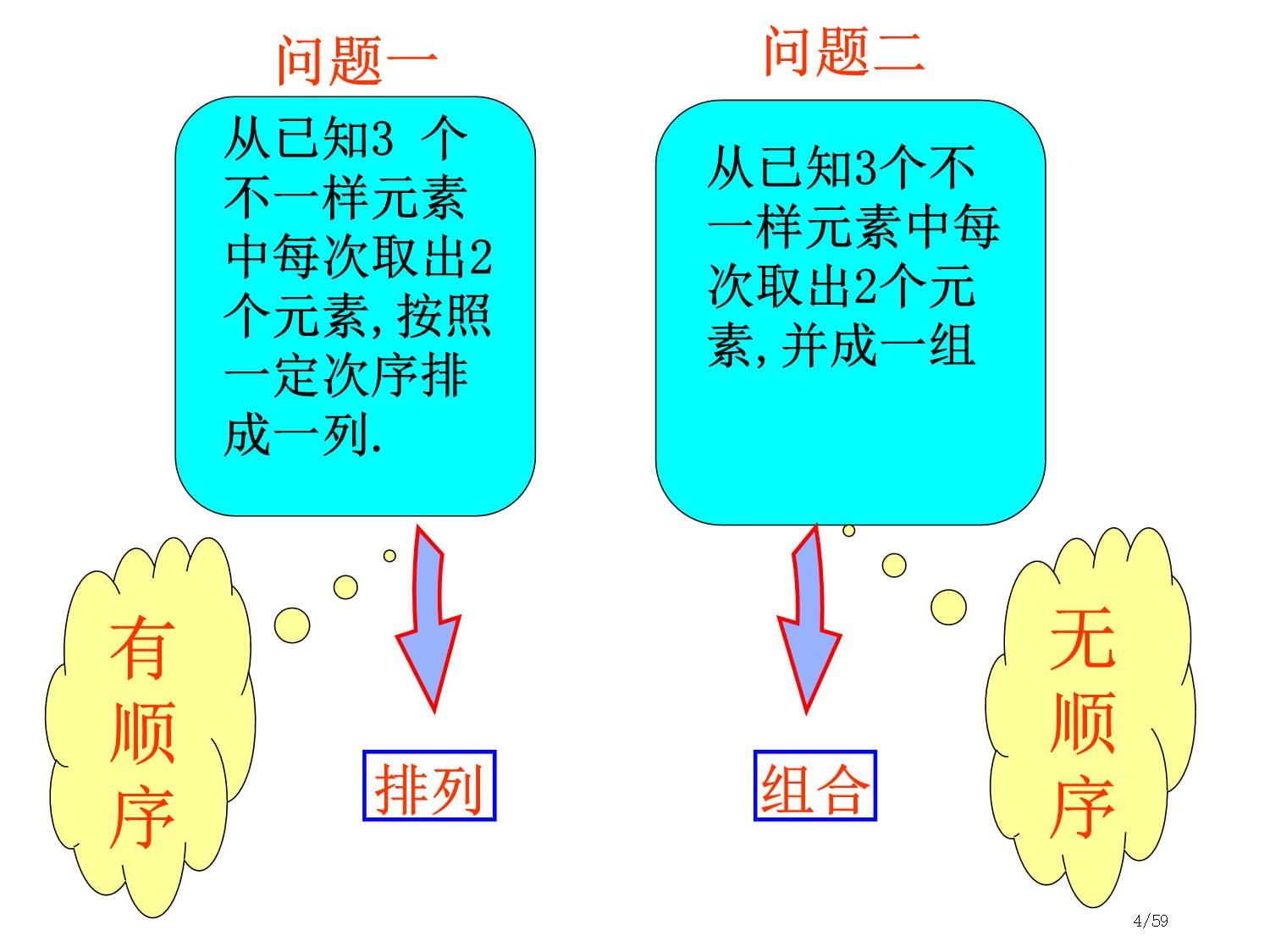
组合(1)1/59组合与组合数公式2/59问题一：从甲、乙、丙3名同学中选出2名去参加某天一项活动，其中1名同学参加早晨活动，1名同学参加下午活动，有多少种不一样选法？问题二：从甲、乙、丙3名同学中选出2名去参加某天一项活动，有多少种不一样选法？甲、乙；甲、丙；乙、丙33/59从已知3个不一样元素中每次取出2个元素,并成一组问题二从已知3

个不一样元素中每次取出2个元素,按照一定次序排成一列.问题一排列组合有顺序无顺序4/59

普通地，从n个不一样元素中取出m（m≤n）个元素并成一组，叫做从n个不一样元素中取出m个元素一个组合.

排列与组合概念有什么共同点与不一样点？

（一）、组合定义:?5/59组合定义:

普通地，从n个不一样元素中取出m（m≤n）个元素并成一组，叫做从n个不一样元素中取出m个元素一个组合．排列定义:普通地，从n个不一样元素中取出m(m≤n)个元素，按照一定次序排成一列，叫做从

n

个不一样元素中取出m个元素一个排列.共同点:都要“从n个不一样元素中任取m个元素”不一样点:排列与元素次序相关，而组合则与元素次序无关.概念讲解6/59思索一:aB与Ba是相同排列还是相同组合?为何?思索二:两个相同排列有什么特点?两个相同组合呢?１）元素相同；２）元素排列次序相同.元素相同概念了解

结构排列分成两步完成，先取后排；而结构组合就是其中一个步骤.思索三:组合与排列有联络吗?7/59判断以下问题是组合问题还是排列问题?

(1)设集合A={a,b,c,d,e}，则集合A含有3个元素子集有多少个?(2)某铁路线上有5个车站，则这条铁路线上共需准备多少种车票?有多少种不一样火车票价？组合问题排列问题组合问题组合是选择结果，排列是选择后再排序结果.8/591.从a,b,c三个不一样元素中取出两个元素全部组合分别是:ab,ac,bc

2.已知4个元素a,b,c,d,写出每次取出两个元素全部组合.abcd

bcd

cd

ab,ac,ad,bc,bd,cd(3个)(6个)概念了解9/59

从n个不一样元素中取出m（m≤n）个元素全部组合个数，叫做从n个不一样元素中取出m个元素组合数，用符号表示.如:从a,b,c三个不一样元素中取出两个元素全部组合个数是:如:已知4个元素a、b、c、d,写出每次取出两个元素全部组合个数是：概念讲解（二）、组合数注意：

是一个数，应该把它与“组合”区分开来．10/591.写出从a,b,c,d四个元素中任取三个元素全部组合abc，abd，acd，bcd.bcddcbacd练一练11/59组合排列abcabdacdbcdabcbaccabacbbcacbaabdbaddabadbbdadbaacdcaddacadccdadcabcdcbddbcbdccdbdcb（三个元素）1个组合，对应着6个排列你发觉了什么?12/59对于，我们能够按照以下步骤进行13/59（三）、组合数公式

排列与组合是有区分，但它们又有联络．

普通地，求从n个不一样元素中取出m个元素排列数，能够分为以下2步：

第1步，先求出从这n个不一样元素中取出m个元素组合数．第2步，求每一个组合中m个元素全排列数．依据分步计数原理，得到：所以：

这里m,n是自然数，且m

n

，这个公式叫做组合数公式．概念讲解14/59组合数公式:从n个不一样元中取出m个元素排列数15/59组合数两个性质:证实:

16/59①公式特征：下标相同而上标差1两个组合数之和，等于下标比原下标多1而上标与大相同一个组合数；②此性质作用：恒等变形，简化运算；③等式表达：“含与不含某元素”分类思想.17/59例1计算：（1）和（2）和例2．计算：解：原式＝18/59D190巩固练习19/59例20/59例．一个口袋内装有大小不一样7个白球和1个黑球.（1）从口袋内取出3个球，使其中含有1个黑球，有多少种取法？（2）从口袋内取出3个球，使其中不含黑球，有多少种取法？（3）从口袋内取出3个球，共有多少种取法？解：（1）取出3个球中有黑球方法数例题讲解21/59例1．一个口袋内装有大小不一样7个白球和1个黑球.（1）从口袋内取出3个球，使其中含有1个黑球，有多少种取法？（2）从口袋内取出3个球，使其中不含黑球，有多少种取法？（3）从口袋内取出3个球，共有多少种取法？解：（1）取出3个球中有黑球方法数⑵取出3个球中无黑球方法数例题讲解22/59例．一个口袋内装有大小不一样7个白球和1个黑球.（1）从口袋内取出3个球，使其中含有1个黑球，有多少种取法？（2）从口袋内取出3个球，使其中不含黑球，有多少种取法？（3）从口袋内取出3个球，共有多少种取法？解：（3）按照黑球分类，②取出3个球中有黑球方法数∴从口袋内取出3个球，共有取法另法，一次取出方法数①取出3个球中无黑球方法数23/59

例2(1)平面内有10个点,以其中每2个点为端点线段共有多少条?10个不一样元素中取2个元素组合数.

10个不一样元素中取2个元素排列数.(2)平面内有10个点,以其中每2个点为端点有向线段共有多少条?24/59

例3(1)有4本不一样书，一个人去借，有多少种不一样借法？

(2)有13本不一样书，其中小说6本，散文4本，诗歌3本，某人借6本，其中有3本小说，2本散文，1本诗歌，问有几个借法？(1)此人所借书能够是一本，二本，三本，四本（本）(2)解：分三个步骤完成，共有（种）25/59

练习：在100件产品中,有98件合格品,2件次品.从这100件产品中任意抽出3件(1)有多少种不一样抽法?100个不一样元素中取3个元素组合数(2)抽出3件中恰好有1件是次品抽法有多少种?从2件次品中抽出1件次品抽法有从98件合格品中抽出2件抽法有26/59

练习在100件产品中,有98件合格品,2件次品.从这100件产品中任意抽出3件(3)抽出3件中最少有1件是次品抽法有多少种?法1含1件次品或含2件次品法2100件中抽3件减98件合格品中抽3件27/591．课外活动小组共13人，其中男生8人，女生5人，而且男、女各指定一名队长，现从中选5人主持某种活动，依以下条件各有多少种选法？(1)只有一名女生；(2)两队长当选；(3)最少有一名队长当选；(4)至多有两名女生当选；(5)既要有队长，又要有女生当选．28/5929/5930/591．将5本不一样书分给4人，每人最少1本，不一样分法种数有(

)A．120种 B．5种C．240种 D．180种组合、排列综合问题31/592．安排3名支教教师去6所学校任教，每校至多2人，则不一样分配方案共有________种(用数字作答)．32/59三、混合问题，先“组”后“排”例3对某种产品6件不一样正品和4件不一样次品,一一进行测试，至区分出全部次品为止，若全部次品恰好在第5次测试时全部发觉,则这么测试方法有种可能？解：由题意知前5次测试恰有4次测到次品，且第5次测试是次品。故有：种可能。33/59练习：某学习小组有5个男生3个女生，从中选3名男生和1名女生参加三项竞赛活动，每项活动最少有1人参加，则有不一样参赛方法______种.解：采取先组后排方法:34/59①主要学习了组合、组合数概念。②利用组合和排列关系得到了组合数公式。n个不一样元素m个元素m个元素全排列第一步组合第二步排列课堂小结：35/59组合中分组问题

6本不一样书，按以下要求各有多少种不一样选法：(1)分给甲、乙、丙三人，每人两本；(2)分为三份，每份两本；(3)分为三份，一份一本，一份两本，一份三本；(4)分给甲、乙、丙三人，一人一本，一人两本，一人三本；(5)分给甲、乙、丙三人，每人最少一本．36/59

[思绪点拨]

(1)是平均分组问题，与次序无关，相当于6本不一样书平均分给甲、乙、丙三人，能够了解为一个人一个人地来取，(2)是“均匀分组”问题，(3)是分组问题，分三步进行，(4)分组后再分配，(5)明确“最少一本”包含“2、2、2型”、“1、2、3型”、“1、1、4型”．37/5938/5939/59

[规律方法]

“分组”与“分配”问题解法(1)本题中每一个小题都提出了一个类型问题，搞清楚类型归属对解题大有裨益，要分清是分组问题还是分配问题，这个是很关键．40/59(2)分组问题属于“组合”问题，常见分组问题有三种：①完全均匀分组，每组元素个数均相等；②部分均匀分组，应注意不要重复，有n组均匀，最终必须除以n！；③完全非均匀分组，这种分组不考虑重复现象．(3)分配问题属于“排列”问题，分配问题能够按要求逐一分配，也能够分组后再分配．41/592．有9本不一样课外书，分给甲、乙、丙三名同学，求在以下条件下，各有多少种分法？(1)甲得4本，乙得3本，丙得2本；(2)一人得4本，一人得3本，一人得2本．42/5943/5944/591．有3张参观券，要在5人中确定3人去参观，不一样方法种数是10

2．6人同时被邀请参加一项活动，必须有些人去，去几人自行决定，共有多少种不一样去法？解：有6类方法，第1类去1人，第2类去2人，第3类去3人，第4类去4人，第5类去5人，第6类去6人，所以共有不一样去法巩固练习45/59

例1一位教练足球队共有17名初级学员,他们中以前没有一人参加过比赛,按照足球比赛规则,比赛时一个足球队上场队员是11人.问:简单组合问题(1)这位教练从这17名学员中能够形成多少种学员上场方案?(2)假如在选出11名上场队员时,还要确定其中守门员,那么教练员有多少种方式做这件事情?(1)没有角色差异共有(2)分两步完成这件事第1步,从17名学员中选出11人上场第2步,从上场11人中选1名守门员46/591、有6本不一样书，分给甲、乙、丙三个人．

(1)假如每人得两本，有多少种不一样分法；

(2)假如一个人得一本，一个人得2本，一个人得

3本有多少种不一样分法；

(3)假如把这6本书分成三堆，每堆两本有多少种不一样分法．2、4名男生6名女生，一共9名实习生分配到高一四个班级担任见习班主任，每班最少有男、女实习生各1名不一样分配方案共有多少种？课后作业：47/59小结2.组合数性质:1.组合数公式:48/59例5个人站成一排⑴共有多少种排法？⑵其中甲必须站在中间，有多少种不一样排法？⑶其中甲、乙两人必须相邻，有多少种不一样排法？⑷其中甲、乙两人不相邻，有多少种不一样排法？⑸其中甲、乙两人不站排头和排尾，有多少种不一样排法？⑹其中甲不站排头，乙不站排尾，有多少种不一样排法？(7)、甲与乙中间必须排2名，有几个排法？49/59例5个人站成一排⑸其中甲、乙两人不站排头和排尾，有多少种不一样排法？解：⑸甲、乙两人不站排头和排尾，则这两个位置可从其余3人中选2人来站，有种排法，剩下人有种排法，共有种排法.(特殊位置预置法)(特殊元素预置法)(排除法)50/59例5个人站成一排⑹其中甲不站排头，乙不站排尾，有多少种不一样排法？解：⑹甲站排头有种排法，乙站排尾有种排法，但两种情况都包含了“甲站排头，乙站排尾”情况，有种排法，所以共有种排法.用直接法，怎样分类？一类：甲站排尾二类：甲站中间所以共有种排法.51/59(7)、甲与乙中间必须排2名，有几个排法？例5个人站