2020-2021学年浙江省杭州市中考数学模拟卷2原卷版+解析(一)

2020-2021学年浙江省杭州市中考数学模拟卷2

学校:姓名：班级：考号：

一、单选题（本题有10小题，每小题4分，共40分每小题只有一个选项是正确的,不选、

多选、错选，均不给分）

1.（2019•浙江杭州市•九年级其他模拟）已知实数a,b,c在数轴上的对应点位置如右

图所示，贝（）

i

O1

H1

<>

A.B.一C.a+c>0D.a+h<0

b-

2.（202（）•浙江杭州市•九年级期末）2016年国庆长假，杭州共接待游客1578.18万人次,

用科学计数法表示1578.18万是（)

A.1.57818x104sB.1.57818xl06C.1.57818X107D.1.57818x10s

3.（2018•浙江杭州市•九年级期末）已知：如图，点D是等腰直角△ABC的重心，其

中NACB=90。，将线段CD绕点C逆时针旋转90。得到线段CE,连结DE,若△ABC

的周长为6,则ADCE的周长为（)

E

B

A.272B.2GC.4D.

4.（2020•浙江杭州市•九年级期末）在样本方差的计算

2

S2-20)2+(/-20)2+•••+（%-20）中，数学10与20分别表示样本的

)

A.样本容量，平均数B.平均数，样本容量

C.样本容量，方差D.标准差，平均数

5.（2019•浙江杭州市•九年级其他模拟）下列计算正确的是（）

A.(a+2Z?)(2a-h^=2a2-2b2B.(6z-Z?)2=a2-b2

C.(Q—b)(—a—/?)=/?—-CTD.(。+242=/+2"+2。2

x+y=5k

6.（2019•杭州绿城育华学校中考模拟）关于x、y的二元一次方程组」.~的解

x-y=9k

也是二元一次方程2x+3y=6的解，则上的值是（）.

3344

A.k=B.k=一C.k=-D.k=—

4433

7.（2020•浙江杭州市•九年级期末）在△ABC中，AB=AC=\O,ZABC=7不,

NA8C的角平分线交AC于点。，则CZ）的长为（）

A.5B.575-5C.15-575D.575-1

X2—6x+93—x

8.（2018•浙江杭州市•中考模拟）方程龙口"十？_32_=0的解的个数为（）

x-\x2-l

A.0个B.1个C.2个D.3个

9.（2020•浙江杭州市•九年级期末）抛物线3/=炉+犬一2与》轴交于4、8两点，A点

在8点左侧，与y轴交于点C.若点E在x轴上，点尸在抛物线上，且以A、C、E、

尸为顶点的四边形是平行四边形，则符合条件的点后有（）

A.1个B.2个C.3个D.4个

10.（2019•浙江杭州市•九年级期末）如图，A8是0。的直径，弦GDLA8于点E,

G是弧8C上任意一点，线段4G与。。交于点汽连接AD,G£>,CG.若

AG-AF=15,CD=2G，则。。的直径为（）

A.4B.275C.|A/3D.373

二、填空题（本题有6小题,每小题5分，共30分）

11.（2019•宁波市第二中学中考模拟）分解因式：a2-4a=.

12.（2020•浙江杭州市•九年级期末）若JTTT有意义，则x的取值范围是

13.（2020•浙江杭州市•九年级期末）一个布袋里有3个只有颜色不同的球，其中2个红

球，1个白球.从布袋里摸出1个球不放回，再摸出1个球，摸出的2个球都是红球的概

率是一.

14.（2019•浙江杭州市•九年级其他模拟）如图，正AABC内接于圆，将A3沿折

叠，AC沿AC折叠.若该圆的半径为2石，则图中阴影部分的面积为.

15.（2019•浙江杭州市•九年级其他模拟）如图，在正方形ABCD中，有面积为4的正

方形EFG”和面积为2的正方形PQMN、点E、F、P、Q分别在边

AB.BC、CD、AO上，点M、N在边HG上，且组成的图形为轴对称图形，则正

方形A8C。的面积为.

16.（2020•浙江杭州市•九年级期末）如图，已知反比例函数＞=-'的图象与直线＞=

x

kx（*＜0）相交于点4、B,以A5为底作等腰三角形，使NAC8=120。，且点C的位

置随着”的不同取值而发生变化，但点C始终在某一函数图象上，则这个图象所对应

的函数解析式为一.

三、解答题（本题有8小题，共80分.解答需写出必要的文字说明、演算步骤或证明过程）

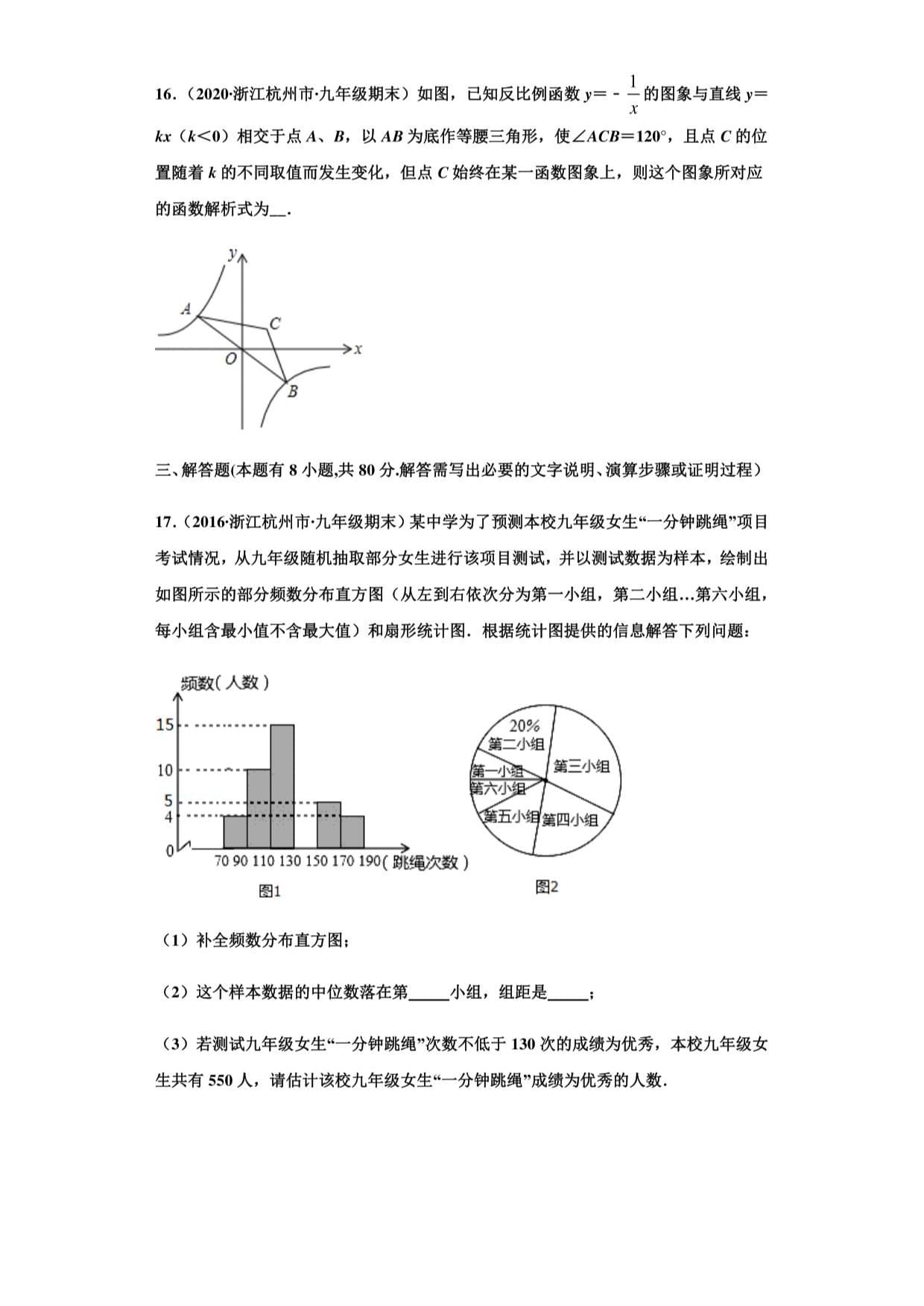
17.（2016•浙江杭州市•九年级期末）某中学为了预测本校九年级女生“一分钟跳绳”项目

考试情况，从九年级随机抽取部分女生进行该项目测试，并以测试数据为样本，绘制出

如图所示的部分频数分布直方图（从左到右依次分为第一小组，第二小组…第六小组,

每小组含最小值不含最大值）和扇形统计图.根据统计图提供的信息解答下列问题：

（1）补全频数分布直方图；

（2）这个样本数据的中位数落在第小组，组距是；

（3）若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀，本校九年级女

生共有550人，请估计该校九年级女生“一分钟跳绳”成绩为优秀的人数.

18.(2021•浙江杭州市•九年级期末)已知二次函数y=(x+m)(x-l)的图象经过点

(2.-3).

(1)求这个二次函数的表达式.

(2)画出这个函数的图象，并利用图象解决下列问题:

①直接写出方程(％+根)(％-1)=-3的解.

②当x满足什么条件时，y〉0.

19.(2020•浙江杭州市•九年级期末)如图，正方形ABCD和正方形4£FG有公共点A,

点8在线段QG上，

(1)判断DG与破的位置关系，并说明理由

（2）若正方形ABCD的边长为2,正方形型G的边长为2夜，求BE的长.

20.（2020•浙江杭州市•九年级期末）如图，在平面直角坐标系中，。为原点，直线AB

分别交x轴正半轴、y轴负半轴于点B,A,与反比例函数的图象交于点C,D,CE1X

2R

轴与点E.cosNA8O=年，AB=5OE=\.

（1）求直线AB和反比例函数的解析式;

（2）求tan/OC。的值.

21.（2019•浙江杭州市•九年级期末）如图，在中，ZC=9O°,以BC为直

径的。。交A6于点D,过点D作乙位用=乙4,交AC于点E.

(1)求证：是的切线；

3

(2)若BC=15,tanA=-,求OE的长.

22.(2019•浙江杭州市•九年级其他模拟)如图，已知一个三角形纸片ABC,边的长

为8,BC边上的高为6,和NC都为锐角，M为A5一动点(点M与点A、B不

重合)，过点M作MN〃3C,交AC于点N,在AAMN中，设MN的长为x,MN上

的高为h.

(1)请你用含x的代数式表示h.

(2)将AAMN沿MN折叠，使AAW落在四边形8CW所在平面，设点A落在平

面的点为4,AA、MN与四边形BCNM重叠部分的面积为y,当x为何值时，y最大，

最大值为多少?

23.(2020•浙江杭州市•九年级其他模拟)如图1,在矩形ABCD中，点E以lcm/s的速

度从点A向点D运动，运动时间为t(s),连结BE,过点E作EF1BE,交CD于F,

以EF为直径作。O.

(1)求证：Z1=Z2；

(2)如图2,连结BF,交。O于点G,并连结EG.已知AB=4,AD=6.

①用含t的代数式表示DF的长

②连结DG,若AEGD是以EG为腰的等腰三角形，求t的值;

(3)连结OC,当tanNBFC=3时，恰有OC〃EG,请直接写出tan/ABE的值.

图1图2

2020-2021学年浙江省杭州市中考数学模拟卷2

学校:姓名：班级：考号：

一、单选题(本题有10小题，每小题4分，共40分每小题只有一个选项是正确的,不选、

多选、错选，均不给分)

1.(2019•浙江杭州市•九年级其他模拟)已知实数a,b,c在数轴上的对应点位置如右

图所示，贝U()

b,

41

1,

A.|«|<1B.->-lC.a+c>0D.a+b<0

b

【答案】D

解：由图可知：

-2<a<-l<b<0<c<l,

A、同>1,故错误，不符合题意；

B、-<-1,故错误，不符合题意；

b

C、a+c<0,故错误，不符合题意；

D、a+h<Q,故正确，符合题意；

故选D.

2.（2020•浙江杭州市•九年级期末）2016年国庆长假，杭州共接待游客1578.18万人次，

用科学计数法表示1578.18万是（）

A.1.57818xlO5B.1.57818xlO6C.1.57818xlO7D.1.57818x10s

【答案】C

解：1578.18万=1.57818x107.

故选：C.

3.（2018•浙江杭州市•九年级期末）已知：如图，点D是等腰直角△ABC的重心，其

中NACB=90。，将线段CD绕点C逆时针旋转90。得到线段CE,连结DE,若△ABC

的周长为6,则4DCE的周长为（）

A.272B.2GC.4D.372

【答案】A

解：延长CD交AB于F.如图，

:点D是等腰直角△ABC的重心，

，CF平分AB,CD=2DF,

I15

；.CF=—AB=—•&CA=—CA,

222

.*.CD=-CF=—CA,

33

•.•线段CD绕点C逆时针旋转90。得到线段CE,

；.CD=CE,ZDCE=90°,

...△CDE为等腰直角三角形，

/•△CDE^ACAB,

」.△CDE的周长：ZiCAB的周长=CD：CA=—

3

ACDE的周长=x6=2J2.

3

故选A.

4.（2020•浙江杭州市•九年级期末）在样本方差的计算

S?菁一20）2+（9—20『+…+%-20）］中，数学10与20分别表示样本的

1UL」

（）

A.样本容量，平均数B.平均数，样本容量C.样本容量，方差D.标准差，平均

数

【答案】A

解：『=A[（X'~2°）2+■―20）2+…+（/—20>],

所以样本容量是10,平均数是20.

故选：A-

5.（2019•浙江杭州市•九年级其他模拟）下列计算正确的是（）

A.（a+2b）（2a-b）-2a2-2b2B.（a-Z?）2=a2-b2

C.[a-k^^-a-b）-b1-a1D.+2b）2=a2+lab+2b2

【答案】C

解：A、（a+2Z7）（2«-Z?）=2«2+3^-2Z?2,故错误，不符合题意；

B、（a-b^ai-2ah+b2,故错误，不符合题意；

C、（a-b）（-a-b^b2-a2,故正确，符合题意；

D、（a+»）2="+4。匕+4巨，故错误，不符合题意；

故选C.

x+y=5k

6.（2019•杭州绿城育华学校中考模拟）关于工、丁的二元一次方程组­〜的解

x-y=9k

也是二元一次方程2x+3y=6的解，则%的值是（）.

3344

A.k=B.k=-C.k=-D.k=

4433

【答案】B

x+y=54①

解：1'〜〜

x-y=94②

①+②得：2x=14Z,即47屋

把x=7左代入①得：7k+y=5k,

解得：y=-2k,

则方程组的解为：\x=lkC,，

y=-2k

'x=7k

把《…代入二元一次方程2%+3丁=6中得：

y=-2k

2x7Z+3x（-2Z）=6,

3

解得：k=9,

4

故选B.

7.（2020•浙江杭州市•九年级期末）在△MC中，AB=AC=10,NABC=72°,

NABC的角平分线交AC于点。，则8的长为（）

A.5B.5y/5-5C.15-5^5D.56一1

【答案】C

解：如图，VAB=AC,ZABC=72°,

/.ZC=72°,

.*.ZA=180°-2x72°=36°,

YBD平分NABC,

.\ZABD=ZCBD=36°,

Z.AD=BD,ZBDC=72°,

ABC=BD,

在AABC和仍BCD中，

ZA=ZCBD,ZABC=ZC,

/.△ABC^ABCD,

.ABBC

•»一，

BCCD

设CD=x,则BD=AD=BC=10-x,

.1010—x

••—f

10-xx

解得：x=15+5后（舍）或15-56,

故选C.

工2—6x+93—x

8.(2018•浙江杭州市•中考模拟)方程上。九十?一上广二。的解的个数为()

X-1X2-]

A.0个B.1个C.2个D.3个

【答案】D

解：去分母得：(x-3)2(x+1)+(x-3)=0,

分解因式得:(x-3)[(x-3)(x+1)+11=0,

可得x-3=0或x2-2x-2=0,

解得：x=3或x=l士百，

经检验x=3与x=1±Ji都为分式方程的解，

则分式方程的解的个数为3个，

故选：D.

9.(2020•浙江杭州市•九年级期末)抛物线)，=炉+》—2与x轴交于A、B两点,4点

在8点左侧，与y轴交于点C.若点E在x轴上，点P在抛物线上，且以A、C、E、

尸为顶点的四边形是平行四边形，则符合条件的点E有（)

A.1个B.2个C.3个D.4个

【答案】D

解：由图象可知，满足条件的A、C、E、P为顶点的四边形是平行四边形有四个,

10.（2019•浙江杭州市•九年级期末）如图，是0。的直径，弦于点E,

G是弧BC上任意一点，线段AG与。。交于点凡连接AD,GD,CG.若

AG-A尸=15,CO=26,则0。的直径为（）

A.4B.2亚C.1\/3D.3g

【答案】C

连接AC.BD

•••弦于点E

AC=AD,DE=—CD—A/3

2

NAC0=NAGC

•••ZC4F=ZCAG

△ACF^AAGC

.AC_AF

~AG~~AC

AC2=AG-AF=15,AC=VL5

•••△AOE是直角三角形，NAED=90。,

AE=ylAD2-ED2=V15-3=2G,

•/NBAD=NDAE，/AED=ZADB=90°

AADE^AABD

ADAE,

AD2_15_5A/3

~AE~243~^T

故答案选：C

二、填空题（本题有6小题,每小题5分，共30分）

11.（2019•宁波市第二中学中考模拟）分解因式：/_4〃=

【答案】a（a—4）

解：a2-4a=a（a-4）

12.（2020•浙江杭州市•九年级期末）若JTMT有意义，则》的取值范围是

【答案】x>-l

解：若Jx+1有意义,

则x+l>0,

解得：x>-l.

故答案为：x>-l.

13.（2020•浙江杭州市•九年级期末）一个布袋里有3个只有颜色不同的球，其中2个红

球，1个白球.从布袋里摸出1个球不放回，再摸出1个球，摸出的2个球都是红球的概

率是-.

【答案】:

3

解：画树状图如下：

一共6种可能，两次都摸到红球的有2种情况，

・・・摸出的2个球都是红球的概率是二2二：1

63

故答案为：

3

14.（2019•浙江杭州市•九年级其他模拟）如图，正△ABC内接于圆，将A6沿A8折

叠，AC沿AC折叠.若该圆的半径为26,则图中阴影部分的面积为.

li

【答案】5G

解：:△ABC为正三角形,

•••AB和AC折叠后交于外接圆圆心O,

...阴影部分面积为△BOC的面积，

过O作OD_LBC,垂足为D,

VZBOC=120°,

.•.ZOBC=ZOCB=30°,

AOD=^-OB=75.

•*-BD=y]OB2-OD2=旧，

：.BC=2BD=2V15,

•*-S阴*=~x2>/15x5/5=5>/3>

故答案为：5百.

15.（2019•浙江杭州市•九年级其他模拟）如图，在正方形A3CD中，有面积为4的正

方形EFG”和面积为2的正方形PQMN、点E、F、P、Q分别在边

AB.BC.CD、A。上，点M、N在边”G上，且组成的图形为轴对称图形，则正

方形ABC。的面积为.

解：如图，连接3。，交PQ于R，交HG于S,交EF于K.

正方形ABCO中，有面积为4的正方形EFGH和面积为2的正方形PQMN,

:.EH=EF=2,MQ=QP=叵,

又♦」组成的图形为轴对称图形,

.•.BD为对称轴,

:.MEF、AOP。为等腰直角三角形，四边形EKS"、四边形MSR。为矩形,

:.EK=BK=-EF^\,DR=QR=、PQ=L也,KN=EH=2,RS=MQ=42,

222

1Q

.•.8。=1+2+夜+—应=3+—近，

22

正方形A3C。的面积=1班）2=,*（3+3拒）2=2+2正，

22242

故答案为：—27+—9\/2-.

42

16.(2020•浙江杭州市•九年级期末)如图，已知反比例函数了=-'的图象与直线y=

X

kx(*<0)相交于点A、B,以A6为底作等腰三角形，使NAC5=120。，且点C的位

置随着A的不同取值而发生变化，但点C始终在某一函数图象上，则这个图象所对应

的函数解析式为_.

【答案】y=—

3x

解：连接CO,过点A作ADLc轴于点。，过点C作CE_Lx轴于点E,

•反比例函数y=-‘的图象与直线）,=辰（女＜0）相交于点A、B,AABC是以A8为

x

底作的等腰三角形，ZACB=120°,

：.CO1AB,NCAB=30°,

则NA">+NCOE=90°,

'：ZDAO+ZAOD=90°,

:.NDAO=NCOE,

又：NAOO=/CEO=90°,

:.△kODsXocE、

ODOA厂

•AD-----=tan60°=13，

~EO~CEOC

q

=(6)2=3

S^OCE

•.•点4是双曲线y=•在第二象限分支上的一个动点,

X

SAOCE——,即一xOEy-CE——,

626

1

，OExCE=-,

3

,这个图象所对应的函数解析式为y=2.

故答案为：y=――-

5X

三、解答题（本题有8小题，共80分.解答需写出必要的文字说明、演算步骤或证明过程）

17.（2016•浙江杭州市•九年级期末）某中学为了预测本校九年级女生“一分钟跳绳”项目

考试情况，从九年级随机抽取部分女生进行该项目测试，并以测试数据为样本，绘制出

如图所示的部分频数分布直方图（从左到右依次分为第一小组，第二小组…第六小组,

每小组含最小值不含最大值）和扇形统计图.根据统计图提供的信息解答下列问题：

图1图2

（1）补全频数分布直方图；

（2）这个样本数据的中位数落在第小组，组距是；

（3）若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀，本校九年级女

生共有550人，请估计该校九年级女生“一分钟跳绳”成绩为优秀的人数.

【答案】（1）见解析；（2）三，20.（3）该校九年级女生跳绳成绩优秀的人数为231人.

解：⑴10+20%=50,50-38=12（人）.

频数分布直方图如下,

(2)中位数在第三小组，组距是20.

故答案分别为三，20.

(3)(12+5+4)4-50=42%550x42%=231(人)，

答：该校九年级女生跳绳成绩优秀的人数为231人.

18.(2021•浙江杭州市•九年级期末)已知二次函数了=(%+机)(％-1)的图象经过点

(2.-3).

(1)求这个二次函数的表达式.

(2)画出这个函数的图象，并利用图象解决下列问题:

①直接写出方程(尤+m)(无-1)=一3的解.

②当X满足什么条件时，>>0.

【答案】(I)y=(x-5)(x-l)；(2)①阳=2,x2=4.②x<l或x>5

解：⑴•.•二次函数丁=(%+机)(％—1)的图象经过点(2,—3),

.•.(2+7«)(2-1)=-3.

解得〃2=-5，

y=(x-5)(x-l)；

(2)由五点法可得如图所示:

①由图像可得:

方程/+/?x+c=-3的解是%=2,%=4；

②由图象可得，当y>0时，x<l或无>5.

19.(2020•浙江杭州市•九年级期末)如图，正方形ABCD和正方形AEFG有公共点A,

点8在线段QG上，

(1)判断。G与BE的位置关系，并说明理由

（2）若正方形A8CO的边长为2,正方形AE尸G的边长为2血，求宓的长.

【答案】（1）DG±BE,理由见解析；（2）«

解：⑴DG工BE，

理由如下：•.•四边形A8C。，四边形AEFG是正方形，

:.AB^AD-ZDAB=ZGAE,AE=AG<ZADB=ZA8D=45°，

:.ZDAG=ZBAE,

在△ZMG和中，

AD^AB

<ZDAG=NBAE,

AG=AE

.•.△ZMG三△84E（SAS）.

:.DG=BE,ZADG=ZABE=45°,

ZABD+ZABE=90°,即ZGBE=90°.

DG工BE；

（2）连接GE,

力

D

•.•正方形ABC。的边长为2,正方形AEFG的边长为20，

:.BD=2日GE=4,

设=X，则BG=x—20，

在RtZSBGE中，利用勾股定理可得:

x2+（x-2>f2）2=42,

：.x=0+限

:.BE的长为6+娓.

20.（2020•浙江杭州市•九年级期末）如图，在平面直角坐标系中，。为原点，直线A8

分别交x轴正半轴、y轴负半轴于点8,A,与反比例函数的图象交于点C,D,CEA.X

2R

轴与点E.cosNA8O=学，AB<,OE=\.

（1）求直线AB和反比例函数的解析式;

(2)求tanNOCQ的值.

134

【答案】(1)y=-x-l,y=—；(2)-

22x7

解：（1）•.,cos/ABO=半，AB=75.

，OB=2,

根据勾股定理得：OA=1,

...点B(2,0),点A(0,-1),

设直线AB的表达式为y=kx+b,

0=2k+bk=-

则,,,解得：\2

-\=b

/?=-1

*e•I工线AB：y=­x—I»

VOE=1,

・••点C的横坐标为・1,代入直线AB表达式,

3

得,y=~—»

3

•二点C的坐标为(-1,----),

2

33

・1X(—,

22

3

・••反比例函数表达式为：y=——；

2x

(2)过点O作AB边上的高OF,

VABxOF=OAxOB,

.CF2x12行

•.OF=-产=---,

V55

21.(2019•浙江杭州市•九年级期末)如图，在R/AABC中，ZC=90°,以8c为直

径的0。交AB于点D,过点D作乙M)E=NA,交AC于点E.

(1)求证：DE是的切线;

（2）若BC=15,tanA=-»求OE的长.

4

d

【答案】（1）见解析；（2；।10

解：（1）证明：连接0。,如图，

ZC=90°.

ZA+NB=90。，

,/OB=OD,

:.ZB=ZODB,

而=

，ZADE+ZODB=90°

:.NODE=90。,

/.OD1DE,

/.DE是OO的切线；

,BC3

（2）解：在心△ABC中，tanA==-

4

，AC=-xl5=20,

3

和EC为O。的切线,

ED-DC，

而Z4£>E=NA，

•••DE=AE，

：.AE=CE=DE=-AC=10,

2

即。E的长为10.

22.（2019•浙江杭州市•九年级其他模拟）如图，已知一个三角形纸片A8C,BC边的长

为8,8c边上的高为6,E8和NC都为锐角，M为AB一动点（点M与点A、B不

重合），过点M作肱V〃BC,交AC于点N,在AAMN中，设MN的长为x,MN上

的高为h.

（1）请你用含x的代数式表示h.

（2）将AAAW沿MN折叠，使AAMN落在四边形8OVM所在平面，设点A落在平

面的点为A,AA\MN与四边形BCNM重叠部分的面积为y,当x为何值时，y最大，

最大值为多少？

Ojx

【答案】（I）力=亍；（2）x=?时，y值最大为8.

解：⑴VMN/7BC

/.△AMN^AABC

,hx

♦•­=—

68

,3x

h=—.

4

(2)VAAMN^AAiMN

A△AIMN的边MN上的高为h

①当点Ai落在四边形BCNM内或BC边上时

i133

2

y=S^MN=-MN-h=-x--x=-x^<x<^

224o

②当Ai落在四边形BCNM外时，如图（4<x<8）

设△AiEF的边EF上的高为hi

3

贝!|hi=2h-6=-x-6

2

VEF/7MN

.'.△AIEF^AAIMN

VAAiMN^AABC

.'.△AiEF^AABC

VSAABC=-x6x8=24

2

3v

,彳x-63

,,S^EF=C2--)2X24=-X2-12X+24

62

y—S"MN~S^EF=77无一—(二I?—]2x+24|=—x2+12x—24

，£Vi|lYllNZA/ij£,r8(2