最短路径问题4-课题学习-最短路径问题(育才)课件

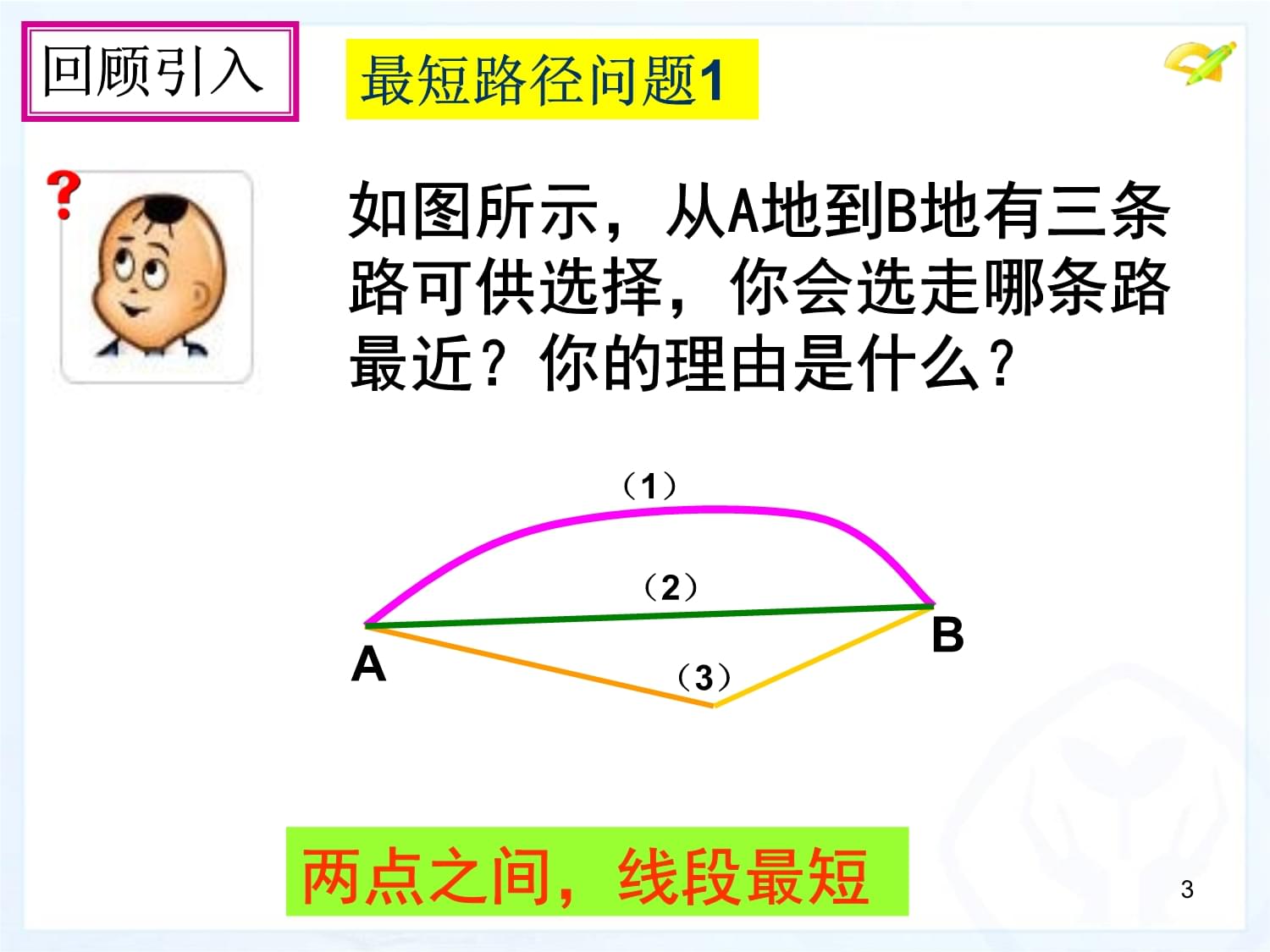
八年级上册13.4

课题学习最短路径问题(第一课时)1最短路径问题是生活中的实际问题，在修路、铺管道的时候，可以起到节约人力、物力、财力的作用，同时它又与我们的数学知识联系紧密。今天我们通过几个案例来学习如何设计最短路径。2回顾引入最短路径问题1两点之间，线段最短如图所示，从A地到B地有三条路可供选择，你会选走哪条路最近？你的理由是什么？AB（1）（2）（3）3回顾引入最短路径问题2垂线段最短如图所示，从直线l外的一点P到直线l的三条路中，你觉得哪条路最近？你的理由是什么？lP（1）（2）（3）4相传，古希腊亚历山大里亚城里有一位久负盛名的学者，名叫海伦．有一天，一位将军专程拜访海伦，求教一个百思不得其解的问题：从图中的A地出发，到一条笔直的河边l饮马，然后到B地．到河边什么地方饮马可使他所走的路径最短？探索新知将军饮马问题精通数学、物理学的海伦稍加思索，利用轴对称的知识回答了这个问题．5(1)若A，B两地在河的两侧时B··AlC·B·将军饮马问题一题多变，引向深刻两点之间线段最短求AC+CB的和最小C6B··AlC(2)若A，B两地在河的同侧时

求AC+CB的和最小将军饮马问题一题多变，引向深刻7思考：能把A、B两点转化到直线l的两侧吗？探索新知B·lA·C将军饮马问题联想问题1的解决方法B··AlC8分析：1、作点B关于直线l的对称点B′，连接CB′。探索新知B·lA·B′C将军饮马问题2、AC+CB=AC+CB′，如果AC+CB′的和最小，那么AC+CB的和最小。9所以：线段AB′与直线l的交点C可使AC+CB的和最小．略证：

如图，在直线l上任取一点C′（与点C不重合），

则C′B=

C′B′

新路径的长度=AC′+C′B

=AC′+C′B′>AB′

=AC+CB

探索新知B·lA·B′CC′将军饮马问题10探索新知A′将军饮马问题B·lA·CB·lA·C方法提示：作点A或点B关于直线l的对称点，所得到的C点位置不变11解：如图（1）作点B关于直线l的对称点B′；（2）连接AB′，与直线l相交于点C．则点C即为所求．探索新知B·lA·B′C将军饮马问题解答过程及作图示范此时路径A-C-B是最短路径。12当A、B两点在直线l的同侧时，线段AB′与直线l的交点C可使AC+CB的和最小。探索新知B·lA·B′C将军饮马问题结论作对称点的作用1.将直线同侧两点问题转化为直线异侧两点问题；2.利用轴对称的性质可以将相等线段转化。13AB街道L1、如图，要在街道旁修建一个卫生站P，便于A,B两区的居民看病。卫生站P应选在何处才能使到它的距离之和最短？学以致用14C学以致用3.已知两点A(2，3),B(4,-3),在y轴上找一点P，使PA+PB最小，并写出点P的坐标。yx学以致用多题一法，加深认识ABA′P-4-3-2-101234

4321

-1-2-3-416(3)若将军要先让马到草地OM吃草，再到河边ON喝水，最后回到出发点A，请画出最短路径。Ml将军饮马问题一题多变，引向深刻NO草地河流17分析：1、建模：点在两直线的内部探索新知B·AC将军饮马问题OMN2、在OM上找点B，在ON上找点C，

使AB+BC+CA的和最小。考虑对称点的作用1.将直线同侧两点问题转化为直线异侧两点问题；2.利用轴对称的性质可以将相等线段转化。18作法：1、作点A关于直线OM的对称点A1，点A关于直线ON的对称点A2，2、连接A1，A2，交OM于B，交ON于C,则路径A-B-C-A是最短路径。探索新知B·AA1C将军饮马问题OMNA2AB+BC+CA的和为什么是最小呢？两点之间线段最短19反证法证明为什么AB+BC+CA的和最小？探索新知B·AA1C将军饮马问题OMNA2情节1：两点之间线段最短20反证法证明为什么AB+BC+CA的和最小？探索新知B·AA1C将军饮马问题OMNA2情节2：两点之间线段最短214.如图，∠AOB内有一点P，在OA,OB上分别找点M,N，使ΔPMN的周长最小？

学以致用OABPMN分析：求PM+MN+NA的和最小22能力提升(4)如图，牧马人从A地出发,先到草地让马吃草，再到河边让马喝水，然后回到B处，请画出最短路径。ABNMH23能力提升(4)如图，牧马人从A地出发,先到草地让马吃草，再到河边让马喝水，然后回到B处，请画出最短路径。ABNMH分析：1、建模：两点在两直线的内部2、作对称点，连线A′B′PG路径A-P-G-B是最短路径。24归纳小结2、解决最短路径问题的方法：作对称点，利用轴对称的性质将线段转化为“两点之间线段最短”来解决。这是数学的化归思想。B··AlC1、建立模型(1)两点在直线异侧(2)两点在直线同侧(3)点在两直线内部25《新观察》P58--59

布置作业26再见27探索新知造桥选址问题如图，A、B两地在一条河的两岸，要在河上造一座桥MN，桥造在何处可使得从A到B的路径AMNB最短？（假设河的两岸是平行的，桥与河垂直）28探索新知造桥选址问题建模问题转化为：当点N在直线b的什么位置时，AM+MN+NB最小？B··AabMN291、如图：一辆汽车在直线公路AB上由A向B行驶，M、N分别表示位于公路AB两侧的村庄，（）当汽车行驶到什么位置时，到村庄M、N的距离之和最短？答：如图，当汽车行驶到P1时，到村庄M、N的距离之和最短。ABMNP1根据：两点之间线段最短。一题多变，引向深刻301、如图：一辆汽车在直线公路AB上由A向B行驶，M、N分别表示位于公路AB两侧的村庄，（2）若村庄M，N在公路AB的两侧，当汽车行驶到什么位置时，到村庄M、N的距离之和最短？N1P2MNAB答：若村庄M，N在公路AB的同侧时，当汽车行驶到P2时，到村庄M、N的距离之和最短。一题多变，引向深刻314.如图，一个旅游船从大桥AB的P处前往山脚下的Q处接游客，然后将游客送往河岸BC上，再返回P处，请画出旅游船的最短路径．ABCPQ山河岸大桥

学以致用多题一法，加深认识32课件说明本节课以数学史中的一个经典问题——“将军饮马问题”为载体开展对“最短路径问题”的课题研究，让学生经历将实际问题抽象为数学的线段和最小问题，再利用轴对称将线段和最小问题转化为“两点之间，线段最短”（或“三角形