山东济南2023年天桥区中考数学一模考试试题（含答案）

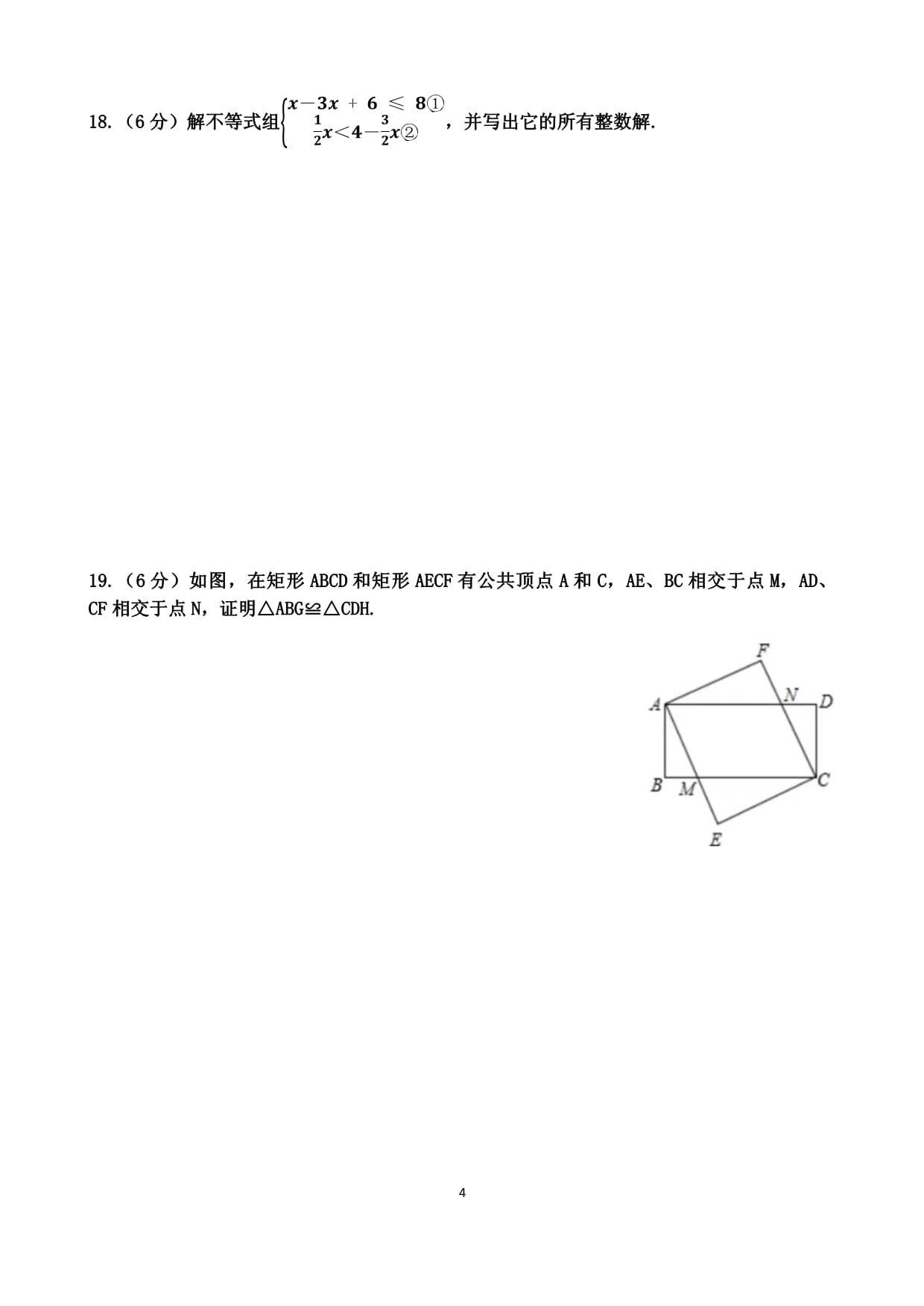
九年级中考数学一模考试试题满分150分时间：120分钟一、单选题。（每小题4分，共40分）1.﹣14A.14B.4C.﹣12.如图所示的石板凳，它的俯视图是（）A.B.C.D.3.一个数是277000000，这个数用科学记数法（）A.277×106B.2.77×107C.2.77×108D.0.277×1094.下列计算中，正确的是（）A.（a3）4=a7B.a2•a6=a8C.a3+a3=a6D.a8÷a4=a25.下列图形中，既是轴对称图形又是中心对称图形的是（）A.B.C.D.6.从1，2，3这三个数中任取两数，分别记为m，n，那么点（m，n）在反比例函数y=6xA.12B.13C.47.如图，若一次函数y=kx+b的图象经过点A（0，﹣1），B（1，1），则不等式kx+b＞1的解集为（）A.x＞1B.x＜1C.x＞0D.x＜0（第7题图）（第8题图）（第9题图）8.如图，在△ABC中，AB=AC，以点C为圆心，CB长为半径画弧，交AB于点B和D，分别以点B，D为圆心，大于12A.3B.10C.11D.239.如图，在平面直角坐标系中，已知⨀D经过原点O，与x轴，y轴交于点A，B两点，点B坐标为（0，23），OC与⨀D交于点C，∠OCA=30°，则图中阴影部分面积为（）A.8π－23B.8π－3C.2π－23D.2π－310.已知二次函数y=mx2－4m2x－3，点P（xp，yp）是该函数图象上一点，当0≤xp≤4时，yp≤﹣3，则m的取值范围是（）A.m≥1或m＜0B.m≥1C.m≤﹣1或m＞0D.m≤﹣1二、填空题。（每小题4分，共24分）11.因式分解：x2－9=.12.黑色袋子中装有质地均匀，大小相同的编号1~15号台球共15个，搅拌均匀后，从袋子中随机摸出1个球，则摸出的球编号为偶数的概率是.13.若关于x的一元二次方程x2－2x+m=0没有实数根，则实数m的取值范围是.14.如图，直线AB交x轴于点C，交反比例函数y=kx（k＞0）的图象A，B两点，过点B作BD⊥y轴，垂足为D，连接CD，若S△BCD=52，则k的值为（第14题图）（第15题图）（第16题图）15.如图，将△ABC沿BC边上的AD平移到△A’B’C’的位置，已知△ABC的面积为9，阴影部分三角形的面积为4，若AA’=1，则A’D等于.16.如图，四边形ABCD是边长为1的正方形，曲线DA1B1C1D1A2是由多段90°的圆心角所对的弧组成的，其中弧DA1的圆心为A，半径为AD，弧A1B1的圆心为B，半径为BA1，弧B1C1的圆心为C，半径为CB1，弧C1D1的圆心为D，半径为DC1弧DA1,弧A1B1,弧B1C1，弧C1D1...的圆心依次按点A，B，C，D循环，则弧C2023D2023的长是.（保留根号）三、解答题。17.（6分）计算25－4sin30°－（1218.（6分）解不等式组x－19.（6分）如图，在矩形ABCD和矩形AECF有公共顶点A和C，AE、BC相交于点M，AD、CF相交于点N，证明△ABG≌△CDH.20.（8分）某小学对部分学生的睡眠情况进行了调查，设每名学生平均每天的睡眠时间为x小时，其中的分组情况是：A组：x＜7.5，B组：7.5≤x＜8，C组：8≤x＜8.5，D组：8.5≤x＜9，E组：x≥9.根据以上信息，解答下列问题：（1）本次共调查了名学生；（2）补全条形统计图；（3）在扇形统计图中，求D组所对应圆心角的度数；（4）该该校有1500名学生，请估计该校睡眠时间不足9小时学生有多少人？21（8分）某数学小组测量古塔DC的高度，如图,在A处用测角仪测得古塔顶端D的仰角为34°，沿AC方向前进15m到达B处，又测得古塔顶点D的仰角为45°，已知测角仪高度AE=BF=1.5m，测量点A，B与古塔DC的底部C在同一水平线上，延长EF交CD于点G，求古塔DC的高度.（精确到1m，参考数据：sin34°≈0.56，cos34°≈0.83，tan34°≈0.67，）22.（8分）如图，D是以AB为直径的⨀O上一点，过点D的切线DE交AB的延长线于点E，过点B作BC⊥DE交AD的延长线于点C，垂足为点F.（1）证明AB=CB；（2）当AB=18，sinA=1323.（10分）某商店购进A，B两种教学仪器，已知A仪器价格是B仪器价格的1.5倍，用450元购买A仪器的数量比用240元购买B仪器数量多2台。（1）求A，B两种仪器单价分别是多少元？（2）该商店购买两种仪器共100台，且A型仪器数量不少于B型仪器数量的1424.（10分）如图，反比例函数y=mx（1）求反比例函数和一次函数解析式；（2）连接OA，OB，求△OAB的面积；（3）如图2，点E是反比例函数图象上A点右侧一点，连接AE，把线段AE绕点A顺时针旋转90°，点E的对应点F恰好也落在这个反比例函数的图象上，求点E的坐标.图1图225.（12分）如图，△ABC和△DBE的顶点B重合，∠ABC=∠DBE=90°，∠BAC=∠BDE=30°，BC=3，BE=2。（1）如图1，当点D，E分别在AB，BC上时，得出结论：ADCE=；直线AD与直线EC的位置关系是（2）如图2，将图1中的△DBE绕点B顺时针旋转一周的过程中，连接AD，EC，其所在直线相交于点F.请说明理由；①（1）中的结论是否仍然成立，若成立，请证明，若不成立，说明理由。②当DF的长度最大时，求线段EC的长度.如图1如图2备用图26.（12分）如图，在平面直角坐标系中，抛物线y=﹣12x2（1）求该抛物线的解析式；（2）正比例函数y=kx的图象分别与线段AB，直线x=3交于点D，E，当△BDO与△OCE相似时，求线段OD的长度；（3）如图2，P是抛物线上位于第一象限的一个动点，在线段OC和直线x=3上是否分别存在点F，G，使B，F，G，P为顶点的四边形是以BF为一边的矩形，若存在，求出点F的坐标，若不存在，说明理由.如图1如图2答案解析一、单选题。（每小题4分，共40分）1.﹣14A.14B.4C.﹣12.如图所示的石板凳，它的俯视图是（D）A.B.C.D.3.一个数是277000000，这个数用科学记数法（C）A.277×106B.2.77×107C.2.77×108D.0.277×1094.下列计算中，正确的是（B）A.（a3）4=a7B.a2•a6=a8C.a3+a3=a6D.a8÷a4=a25.下列图形中，既是轴对称图形又是中心对称图形的是（D）A.B.C.D.6.从1，2，3这三个数中任取两数，分别记为m，n，那么点（m，n）在反比例函数y=6xA.12B.13C.47.如图，若一次函数y=kx+b的图象经过点A（0，﹣1），B（1，1），则不等式kx+b＞1的解集为（A）A.x＞1B.x＜1C.x＞0D.x＜0（第7题图）（第8题图）（第9题图）8.如图，在△ABC中，AB=AC，以点C为圆心，CB长为半径画弧，交AB于点B和D，分别以点B，D为圆心，大于12A.3B.10C.11D.239.如图，在平面直角坐标系中，已知⨀D经过原点O，与x轴，y轴交于点A，B两点，点B坐标为（0，23），OC与⨀D交于点C，∠OCA=30°，则图中阴影部分面积为（C）A.8π－23B.8π－3C.2π－23D.2π－310.已知二次函数y=mx2－4m2x－3，点P（xp，yp）是该函数图象上一点，当0≤xp≤4时，yp≤﹣3，则m的取值范围是（A）A.m≥1或m＜0B.m≥1C.m≤﹣1或m＞0D.m≤﹣1二、填空题。（每小题4分，共24分）11.因式分解：x2－9=（x+3）（x－3）.12.黑色袋子中装有质地均匀，大小相同的编号1~15号台球共15个，搅拌均匀后，从袋子中随机摸出1个球，则摸出的球编号为偶数的概率是71513.若关于x的一元二次方程x2－2x+m=0没有实数根，则实数m的取值范围是m＞1.14.如图，直线AB交x轴于点C，交反比例函数y=kx（k＞0）的图象A，B两点，过点B作BD⊥y轴，垂足为D，连接CD，若S△BCD=52，则k的值为（第14题图）（第15题图）（第16题图）15.如图，将△ABC沿BC边上的AD平移到△A’B’C’的位置，已知△ABC的面积为9，阴影部分三角形的面积为4，若AA’=1，则A’D等于2.16.如图，四边形ABCD是边长为1的正方形，曲线DA1B1C1D1A2是由多段90°的圆心角所对的弧组成的，其中弧DA1的圆心为A，半径为AD，弧A1B1的圆心为B，半径为BA1，弧B1C1的圆心为C，半径为CB1，弧C1D1的圆心为D，半径为DC1弧DA1,弧A1B1,弧B1C1，弧C1D1...的圆心依次按点A，B，C，D循环，则弧C2023D2023的长是2023π.（保留根号）三、解答题。17.（6分）计算25－4sin30°－（12=5－2－2+1=218.（6分）解不等式组x－解不等式①得x≥﹣1解不等式②得x＜2不等式组解集为﹣1≤x＜2整数解为﹣1，0，119.（6分）如图，在矩形ABCD和矩形AECF有公共顶点A和C，AE、BC相交于点M，AD、CF相交于点N，证明△ABG≌△CDH.证明：∵四边形ABCD是矩形∴∠B=∠D=90°AB=CDAD∥BC∵四边形AECF是矩形∴AE∥CF∴四边形AMCN是平行四边形∴AM=CN∴Rt△ABG≌Rt△CDH20.（8分）某小学对部分学生的睡眠情况进行了调查，设每名学生平均每天的睡眠时间为x小时，其中的分组情况是：A组：x＜7.5，B组：7.5≤x＜8，C组：8≤x＜8.5，D组：8.5≤x＜9，E组：x≥9.根据以上信息，解答下列问题：（1）本次共调查了名学生；（2）补全条形统计图；（3）在扇形统计图中，求D组所对应圆心角的度数；（4）该该校有1500名学生，请估计该校睡眠时间不足9小时学生有多少人？（1）20÷20%=100人（2）（3）360°×20100（4）1500×5+21（8分）某数学小组测量古塔DC的高度，如图,在A处用测角仪测得古塔顶端D的仰角为34°，沿AC方向前进15m到达B处，又测得古塔顶点D的仰角为45°，已知测角仪高度AE=BF=1.5m，测量点A，B与古塔DC的底部C在同一水平线上，延长EF交CD于点G，求古塔DC的高度.（精确到1m，参考数据：sin34°≈0.56，cos34°≈0.83，tan34°≈0.67，）延长EF交DC于点H∵∠DHF=90°，EF=AB=15米CH=BF=AE=1.5米设FH=x米∴EH=（15+x）米在Rt△DFH中，∠DFH=45°∴DH=FH=x米在Rt△DHE中，∠DEH=34°tan34°=xx+15x=30.1∴DC=30.1+1.5≈32米22.（8分）如图，D是以AB为直径的⨀O上一点，过点D的切线DE交AB的延长线于点E，过点B作BC⊥DE交AD的延长线于点C，垂足为点F.（1）证明AB=CB；（2）当AB=18，sinA=13（1）∵DE是⨀O的切线∴OD⊥DE∵OD∥BC∴OD∥BC∴∠ODA=∠C∵OA=OD∴∠ODA=∠A∴∠A=∠C∴AB=BC（2）连接BD，则∠ADB=90°在Rt△ABD，sinA=BDAB=13∴BD=6∵0B=0D∴∠ODB=∠OBD∵∠OBD+∠A=∠FDB+∠ODB=90°∴∠A=∠FDBsin∠BDF=BFBD=∴BF=2∴△EBF∽△EOD∴BEOE=BFOD即BEBE=18∴EF=823.（10分）某商店购进A，B两种教学仪器，已知A仪器价格是B仪器价格的1.5倍，用450元购买A仪器的数量比用240元购买B仪器数量多2台。（1）求A，B两种仪器单价分别是多少元？（2）该商店购买两种仪器共100台，且A型仪器数量不少于B型仪器数量的14（1）解设B型单价为x元，则A型单价为1.5x元4501.5xx=30经检验，x=30是原方程的解1.5x=1.5×30=45元（2）解设A型仪器数量为a台，B型仪器为（100－a）台。a≥14a≥25A型仪器至少购买25台，此时总费用=25×45+30×（100－25）=3375元24.（10分）如图，反比例函数y=mx（1）求反比例函数和一次函数解析式；（2）连接OA，OB，求△OAB的面积；（3）如图2，点E是反比例函数图象上A点右侧一点，连接AE，把线段AE绕点A顺时针旋转90°，点E的对应点F恰好也落在这个反比例函数的图象上，求点E的坐标.图1图2（1）将A（1，3）代入反比例函数y=m解得m=1×3=3∴y=3将B（n，1）代入y=3n=3将A（1，3），点B（3，1）代入y=kx+bk+b=3∴y=﹣x+4（2）△OAB的面积=（1+3）×（3－1）÷2=4（3）设点E（m，3m），F（n，3由旋转知：△AEF为等腰直角三角形（m∴E（6，1225.（12分）如图，△ABC和△DBE的顶点B重合，∠ABC=∠DBE=90°，∠BAC=∠BDE=30°，BC=3，BE=2。（1）如图1，当点D，E分别在AB，BC上时，得出结论：ADCE=；直线AD与直线EC的位置关系是（2）如图2，将图1中的△DBE绕点B顺时针旋转一周的过程中，连接AD，EC，其所在直线相交于点F.请说明理由；①（1）中的结论是否仍然成立，若成立，请证明，若不成立，说明理由。②当DF的长度最大时，求线段EC的长度.如图1如图2备用图（1）3AD⊥EC（2）①成立∵△ABC和△DBE的顶点B重合，∠ABC=∠DBE=90°，∠BAC=∠BDE=30°∴ABBC=BDBE=∴ABBC=3∵∠ABC=∠DBE=90°∠ABC－∠CBD=∠DBE－∠CBD∴∠ABD=∠CBE∴△ABD∽△BCE∴ADCE=BDBE=∴∠ACF=180°－60°－∠BCE=120°－∠BAD=120°－（30°+∠CAF）=90°－∠CAF∴∠ACF+∠CAF=90°∴∠AFC=90°∴AD⊥EC（3）EC=33226.（12分）如图，在平面直角坐标系中，抛物线y=﹣12x2（1）求该抛物线的解析式；（2）正比例函数y=kx的图象分别与线段AB，直线x=3交于点D，E，当△BDO与△OCE相似时，求线段OD的长度；（3）如图2，P是抛物线上位于第一象限的一个动点，在线段OC和直线x=3上是否分别存在点F，G，使B，F，G，P为顶点的四边形是以BF为一边的矩形，若存在，求出点F的坐标，若不存在，说明理由.如图1如图2（1）将A（﹣2，0），B（0，4）代入y=﹣12x2﹣2－∴y=﹣12x2（2）当△BDO与△OCE相似∴∠ODB=∠OCE=90°KAB×KDE=﹣1即4－00KDE=﹣1正比例函数y=﹣12联立y=﹣12xyOD=（﹣85（2，0）或（201－11九年级中考数学二模考试试题满分150分时间：120分钟一、单选题。（每小题4分，共40分）1.－3的绝对值是（）A.－3B.3C.13D.﹣2.如图是某几何体的三视图，该几何体是（）A.B.C.D.3.“丝绸之路经济带”首个实体平台——中哈（连云港）物流合作基地的年最大装卸能力达到410000标箱，其中“410000”用科学记数法表示为（）A.0.41×106B.4.1×105C.41×104D.4.1×1064.将一副三角尺按如图摆放，点E在AC上，点D在BC的延长线上，EF∥BC，∠B＝∠EDF＝90°,∠A＝45°,∠F＝60°,则∠CED的度数是（）A.15°B.20°C.25°D.30°（第4题图）（第6题图）5.许多数学符号蕴含着对称美，在下列数学符号中，既是轴对称图形，又是中心对称图形的符号是（）A.B.C.D.6.实数a，b在数轴上对应点的位置如图所示，下列结论正确的是（）A.ab＞07.小冰和小雪自愿参加学校组织的课后托管服务活动，随机选择自主阅读、体育活动、科普活动三项中的某一项，那么小冰和小雪同时选择“体育活动”的概率为（）A.13B.23C.18.如图，在平面直角坐标系中，△ABC的顶点都在格点上，如果将△ABC先沿y轴翻折，再向下平移3个单位长度，得到△A’B’C’，那么点B的对应点B’的坐标为（）A.（2，﹣3）B.（4，3）C.（﹣1，﹣3）D.（1，0）(第8题图)(第9题图)9．如图，已知矩形AOBC的三个顶点的坐标分别为O（0，0），A（0，3），B（4，0），按以下步骤作图：①以点O为圆心，适当长度为半径作弧，分别交OC，OB于点D，E；②分别以点D，E为圆心，大于12A.（4，43）B.（43，4）C.（5310.已知二次函数y=﹣x2+2x+3，截取该函数图象在0≤x≤4间的部分记为图象G，设经过点（0，t）且平行于x轴的直线为l，将图象G在直线l下方的部分沿直线l翻折，图象G在直线上方的部分不变，得到一个新函数的图象M，若函数M的最大值与最小值的差不大于5，则t的取值范围是（）A.0≤x≤1B.﹣1≤x≤1C.﹣2≤x≤0D.﹣1≤x≤0二．填空题。（每小题4分，共24分）11.分解因式：m2－3m=.12.个不透明的布袋中装有3个红球，5个黄球，2个白球，每个球除颜色外都相同，任意摸出一球，摸到红球的概率为．13.已知a，b为两个连续的整数，且a＜5＜b，则ba=．14.代数式52x－1与代数式315.如图，一张扇形纸片的圆心角为90°，半径为6，C是OA的中点，CD∥OB，则图中阴影部分的面积为．（第15题图）（第16题图）16.如图，正方形ABCD中，AB＝4，点E是对角线BD上一点，连接AE，过点E作EF⊥AE，交BC于点F，连接AF，交BD于点M，将△EFM沿EF翻折，得到△EFN，连接AN，交EF于点G，若点F是BC边的中点，则线段AN的长是．三、解答题。17.（6分）计算（12）﹣1+（2023+π）018.（6分）解不等式组2（19.（6分）如图，在平行四边形ABCD中，点E，F在对角线BD上，BA⊥AF，DC⊥CE．求证：DF＝BE.20.（8分）某学校九年级共1200名学生，为了解该年级学生的视力情况，从中随机抽取40名学生的视力数据作为样本，视力在4.5≤x≤5.0范围内的数据如下：4.74.54.95.04.64.84.54.94.94.84.54.54.95.0根据上面提供的信息，回答下列问题：（1）统计表中的a＝，b＝．（2）请补全条形统计图．（3）写出这40名同学视力的中位数是．（4）根据抽样调查结果，请估计该校九年级学生视力为“E级”的有多少人？21（8分）如图，某建筑物AD楼顶立有高为6米的广告牌DE，小雪准备利用所学的三角函数知识估测此建筑物的高度，她从地面点B处沿坡度为i＝3：4的斜坡BC步行15米到达点C处，测得广告牌底部点D的仰角为45°，广告牌顶部点E的仰角为53°．（小雪的身高忽略不计，坡面的铅直高度与水平宽度的比称为坡度，参考数据：sin53≈0.8，cos53≈0.6，tan53≈1.3）（1）求点C距离水平地面的高度；（2）求建筑物AD的高度．22.（8分）如图，AB是⨀O的直径，点C是⨀O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB于点F，连接BE.（1）求证：AC平分∠DAB；（2）若AD=8，AC=45，求线段BE的长．23.（10分）“4G改变生活，5G改变社会”，不一样的5G手机给人们带来了全新的体验，某营业厅现有A，B两种型号的5G手机出售，售出1部A型、1部B型手机共获利600元，售出3部A型、2部B型手机共获利1400元．（1）求A、B两种型号的手机每部利润各是多少元；（2）某营业厅再次购进A，B两种型号手机共20部，其中B型手机的数量不超过A型手机数量的2324.（10分）如图，在直角坐标系中，直线y=﹣34x与反比例函数y=k（1）求反比例函数的表达式；（2）将直线y=﹣34x（3）E是y轴正半轴上的一点，F是平面内任意一点，使以点A，B，E，F为顶点的四边形是矩形，请求出所有符合条件的点E的坐标．25.（12分）如图，△ABC是等腰直角三角形，∠ACB=90°，BC=25，点D为平面内任意一点，将线段CD绕点C逆时针方向旋转90°得到线段CE，连接AE．（1）若点D为△ABC内部任意一点时，①如图1，判断线段AE与BD的数量关系并给出证明；②如图2，连接DE，当点E，D，B在同一直线上且BD＝2时，求线段CD的长；（2）如图3，直线AE与直线BD相交于点P，当AD＝AC时，延长AC到点F，使得CF＝AC，连接PF，请直接写出PF的取值范围．图1图2图326.（12分）如图，抛物线y=ax2+bx+6与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．（1）求抛物线的解析式；（2）若在线段BC上存在一点M，使得∠BMO＝45°，过点O作OH⊥OM交CB的延长线于点H，求点H的坐标；（3）在（2）的条件下，点P是y轴正半轴上的一个动点，连接PM，过M做MQ⊥PM交x轴与Q，N是PQ的中点，求BN的最小值．备用图答案解析一．单选题。（每小题4分，共40分）1.－3的绝对值是（B）A.－3B.3C.13D.﹣2.如图是某几何体的三视图，该几何体是（C）A.B.C.D.3.“丝绸之路经济带”首个实体平台——中哈（连云港）物流合作基地的年最大装卸能力达到410000标箱，其中“410000”用科学记数法表示为（B）A.0.41×106B.4.1×105C.41×104D.4.1×1064.将一副三角尺按如图摆放，点E在AC上，点D在BC的延长线上，EF∥BC，∠B＝∠EDF＝90°,∠A＝45°,∠F＝60°,则∠CED的度数是（A）A.15°B.20°C.25°D.30°（第4题图）（第6题图）5.许多数学符号蕴含着对称美，在下列数学符号中，既是轴对称图形，又是中心对称图形的符号是（D）A.B.C.D.6.实数a，b在数轴上对应点的位置如图所示，下列结论正确的是（B）A.ab＞07.小冰和小雪自愿参加学校组织的课后托管服务活动，随机选择自主阅读、体育活动、科普活动三项中的某一项，那么小冰和小雪同时选择“体育活动”的概率为（C）A.13B.23C.18.如图，在平面直角坐标系中，△ABC的顶点都在格点上，如果将△ABC先沿y轴翻折，再向下平移3个单位长度，得到△A’B’C’，那么点B的对应点B’的坐标为（D）A.（2，﹣3）B.（4，3）C.（﹣1，﹣3）D.（1，0）(第8题图)(第9题图)9．如图，已知矩形AOBC的三个顶点的坐标分别为O（0，0），A（0，3），B（4，0），按以下步骤作图：①以点O为圆心，适当长度为半径作弧，分别交OC，OB于点D，E；②分别以点D，E为圆心，大于12A.（4，43）B.（43，4）C.（5310.已知二次函数y=﹣x2+2x+3，截取该函数图象在0≤x≤4间的部分记为图象G，设经过点（0，t）且平行于x轴的直线为l，将图象G在直线l下方的部分沿直线l翻折，图象G在直线上方的部分不变，得到一个新函数的图象M，若函数M的最大值与最小值的差不大于5，则t的取值范围是（D）A.0≤x≤1B.﹣1≤x≤1C.﹣2≤x≤0D.﹣1≤x≤0二．填空题。（每小题4分，共24分）11.分解因式：m2－3m=m（m－3）.12.个不透明的布袋中装有3个红球，5个黄球，2个白球，每个球除颜色外都相同，任意摸出一球，摸到红球的概率为31013.已知a，b为两个连续的整数，且a＜5＜b，则ba=9．14.代数式52x－1与代数式315.如图，一张扇形纸片的圆心角为90°，半径为6，C是OA的中点，CD∥OB，则图中阴影部分的面积为3π．（第15题图）（第16题图）16.如图，正方形ABCD中，AB＝4，点E是对角线BD上一点，连接AE，过点E作EF⊥AE，交BC于点F，连接AF，交BD于点M，将△EFM沿EF翻折，得到△EFN，连接AN，交EF于点G，若点F是BC边的中点，则线段AN的长是1023三、解答题。17.（6分）计算（12）﹣1+（2023+π）0=2+1－1+3=518.（6分）解不等式组2（解：由①得x≤5，由②得x>2，这个不等式组的解集为2<x≤5，不等式组的整数解是3，4，5．19.（6分）如图，在平行四边形ABCD中，点E，F在对角线BD上，BA⊥AF，DC⊥CE．求证：DF＝BE.证明：∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD，∴∠ABD＝∠CDB，∵AF⊥BA，DC⊥CE，∴∠BAF＝∠DCE＝90°∴△ABF≌△CDE，∴BF＝DE，∴BF－EF＝DE－EF，∴BE＝DF．20.（8分）某学校九年级共1200名学生，为了解该年级学生的视力情况，从中随机抽取40名学生的视力数据作为样本，视力在4.5≤x≤5.0范围内的数据如下：4.74.54.95.04.64.84.54.94.94.84.54.54.95.0根据上面提供的信息，回答下列问题：（1）统计表中的a＝，b＝．（2）请补全条形统计图．（3）写出这40名同学视力的中位数是．（4）根据抽样调查结果，请估计该校九年级学生视力为“E级”的有多少人？（1）6，25；（2）：（3）4.55，（4）1200×25%＝300（人），答：该校九年级学生视力为“E级”的约有300人．21（8分）如图，某建筑物AD楼顶立有高为6米的广告牌DE，小雪准备利用所学的三角函数知识估测此建筑物的高度，她从地面点B处沿坡度为i＝3：4的斜坡BC步行15米到达点C处，测得广告牌底部点D的仰角为45°，广告牌顶部点E的仰角为53°．（小雪的身高忽略不计，坡面的铅直高度与水平宽度的比称为坡度，参考数据：sin53≈0.8，cos53≈0.6，tan53≈1.3）（1）求点C距离水平地面的高度；（2）求建筑物AD的高度．解：（1）如图，过C作CG⊥AB于G，∵斜坡AB的坡度i=CGBG=3∴CG＝9（米），∴点C距离水平地面的高度为9米．（2）如图，过C作CF⊥AE于F，∵CF⊥AE，CG⊥AB，EA⊥AB，∴∠CGA＝∠GAF＝∠AFC＝90°，∴四边形AFCG为矩形，∴AF＝CG＝9（米），设DF＝x米在Rt△DCF中，∠DCF＝45°，∴CF＝DF＝x米．在Rt△ECF中，∠ECF＝53°，∴tan∠ECF=EFCF=x+6解得x≈20．∴DF＝20米，∴AD＝AF＋DF＝9＋20＝29（米），∴建筑物AD的高度约为29m．22.（8分）如图，AB是⨀O的直径，点C是⨀O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB于点F，连接BE.（1）求证：AC平分∠DAB；（2）若AD=8，AC=45，求线段BE的长．∵PD为⨀O的切线，∴OC⊥DP，∵AD⊥DP，∴∠ADC＝∠OCP＝90°∴OC∥AD，∴∠DAC＝∠OCA，∵OA＝OC，∴∠OAC＝∠OCA，∴∠OAC＝∠DAC，∴AC平分∠DAB；（2）解：如图，连接OE∵AB是⨀O的直径，AD⊥DP，∴∠ACB＝∠D＝90°∵∠OAC＝∠DAC，∴△BAC∽△CAD，∴ABAC=∴AB45∴AB＝10，∴OB＝OE＝5∵CE平分∠ACB，∴∠BCE=12∵弧BE=弧BE，∴∠BOE＝2∠BCE＝90°∴△ACB为等腰直角三角形，∴BE=2OB=5223.（10分）“4G改变生活，5G改变社会”，不一样的5G手机给人们带来了全新的体验，某营业厅现有A，B两种型号的5G手机出售，售出1部A型、1部B型手机共获利600元，售出3部A型、2部B型手机共获利1400元．（1）求A、B两种型号的手机每部利润各是多少元；（2）某营业厅再次购进A，B两种型号手机共20部，其中B型手机的数量不超过A型手机数量的23解：（1）设A种型号手机每部利润是x元，B种型号手机每部利润是y元，由题意得：x+y解得x=答：A种型号手机每部利润是200元，B种型号手机每部利润是400元；（2）设购进A种型号的手机a部，则购进B种型号的手机（20－a）部，获得的利润为w元，w=200a+400（20－a）=﹣200a+8000，∵B型手机的数量不超过A型手机数量的220－a≤23解得a≥12，∴w随a的增大而减小，∴当a＝12时，w取得最大值，此时w＝－2400＋8000＝5600，20－a＝20－12＝8．答：营业厅购进A种型号的手机12部，B种型号的手机8部时获得最大利润，最大利润是5600元．（10分）如图，在直角坐标系中，直线y=﹣34x与反比例函数y=k（1）求反比例函数的表达式；（2）将直线y=﹣34x（3）E是y轴正半轴上的一点，F是平面内任意一点，使以点A，B，E，F为顶点的四边形是矩形，请求出所有符合条件的点E的坐标．解：（1）令一次函数y=﹣34x中y＝3，则3=﹣3解得：x＝－4，即点A的坐标为（﹣4，3），∵点A（﹣4，3）在反比例函数的图象y=k∴k=﹣12，∴反比例函数的表达式为y=﹣12x（2）连接AC、BC如图所示．设平移后直线CD的解析式为y=﹣34x+b，∴点C（0，b）∵该直线平行直线AB，∴S△ABD=S△ABC∵△ABD的面积为16，∵点A、点B关于原点对称，∴点B（4,﹣3）∴S