数学说题(谢明初老师)

数学说题:意义与流程

广东省课程改革指导委员会专家教育部义务教育教科书审查委员会专家2021/5/91一、问题与数学

1.问题是数学的心脏,思维始于问题

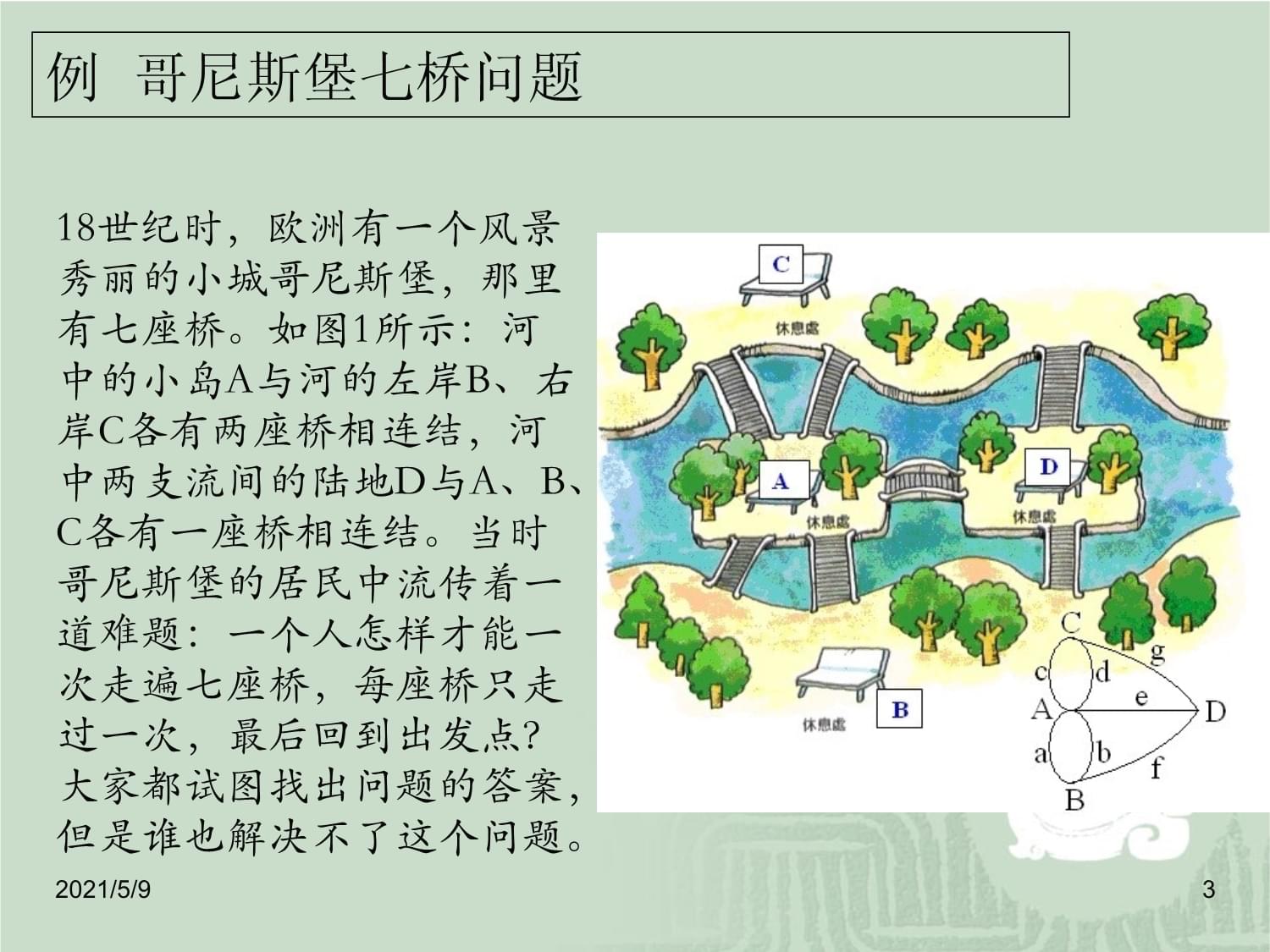
2021/5/92例哥尼斯堡七桥问题18世纪时，欧洲有一个风景秀丽的小城哥尼斯堡，那里有七座桥。如图1所示：河中的小岛A与河的左岸B、右岸C各有两座桥相连结，河中两支流间的陆地D与A、B、C各有一座桥相连结。当时哥尼斯堡的居民中流传着一道难题：一个人怎样才能一次走遍七座桥，每座桥只走过一次，最后回到出发点？大家都试图找出问题的答案，但是谁也解决不了这个问题。

2021/5/93四色问题任意一张分区地图，最少需要多少种颜色来涂，使得相邻的区域都涂上不同颜色？由下图我们清楚地知道至少需要4种颜色：2021/5/94

任意一張分區地圖，只用4種顏色來著色夠嗎？

一百多年前，就有人針對這個問題提出了一個臆測：「任意一張分區地圖，都只需要4種顏色來著色。」是誰首先提出四色問題的？沒人知道。但最先有記錄可尋的是1852年，英國數學家摩根（A.deMorgan）給愛爾蘭數學家漢彌頓（W.Hamilton）的一封信。信中他提到有個學生（F.Guthrie）跟他提起地圖著色的問題；學生說四色就夠了，但摩根找不到任何的證明。四色問題在當時並沒有立即引起大家的注意。一直到26年後，英國數學家凱利（A.Cayley）發現事情並不如大家所想的那麼簡單，四色問題才引起了熱烈的討論。2021/5/95次年，康沛（A.Kempe）宣佈他證明了四色定理。但是11年後，希悟（P.Heawood）卻發現了康沛證明中的一個漏洞，四色定理又變回了四色問題。數學家們繼續努力了將近一個世紀，在1976年，美國伊利諾大學的兩位數學教授阿倍尔（K.Appel）及哈根（W.Haken）才利用计算机的辅助将这个问题解决。2021/5/962.问题解决是数学教育改革的焦点1980年4月,以美国数学教师全国联合会(NCTM)的名义，公布了一份名曰《行动纲领–80年代数学教育的议程》的文件，首次提出必须把问题解决(problemsolving)作为80年代中学数学的核心。2021/5/97在1980年8月的第四届国际数学会议上，美国数学教师协会提出了80年代中学数学教育行动计划的八点建议，指出80年代中学数学教育改革焦点是培养学生问题解决的能力，这种力量衡量个人和国家数学水平的标志。2021/5/98到1988年召开的第六届国际数学教育会议上，则将问题解决列为大会的七个主要研究课题之一，在课题报告中，几次明确提出问题解决仿真化和应用必须成为从中学到大学的所有数学课程的一部份。这样，在美国和国际数学教育会议的推动下，问题解决受到了世界各国数学界普遍重视，不仅成为国际数学教育界研究的重要课题，而且是继“新数运动”和“回到基础”之后兴起的80年代和90年代国际数学教育发展的潮流。2021/5/99二、从说课到说题1.有中国特色的教研活动

“说题”活动有利于提高师范生的数学解题能力和数学教学能力，有利于数学师范生综合素质的提高，促进其教师专业的发展。2.讲课与说课3.说课与说题

2021/5/910“说题”是教师基于数学教育理论，面向同行、专家或教研人员，以口头表达为主，以其他方法为辅，表述对某个数学问题的解题思路和教学策略的看法，包括问题的产生和运用背景、问题的表层与深层涵义、问题解决的方法与策略、问题解决的心理障碍、问题的数学价值与教育意义、问题的拓展与创新等。2021/5/9114.解题与说题2021/5/912三、说题案例1

问题已知函数则它的最大值为()(D)(A)(C)(B)22021/5/913导入语数学的世界里并不缺少美，而是缺少一个善于思考的大脑。数学本身是美妙的，也可以学得很美妙。在数学的世界里，你会发现数学的美妙千变万化，数学的美妙让你流连忘返，数学的美妙让你如痴如醉。这种种数学的美妙，我们可以称之为“数学美”。正因为这“数学美”，科学得以巨大飞跃，社会得以高速发展，人类得以主宰世界。在数学的小世界里，你会发现另外一番大世界。在浩瀚无垠的数学题海里，我要说的这个小题，淋漓尽致的诠释了她的美妙，而这仅仅是冰山一角。只要你热爱数学，只要你善于思考，数学的世界就是美的世界。2021/5/9141.问题背景

它选自2012年江苏南通数学模拟卷三，知识点涉及已知函数求最值问题，可考查学生的观察与归纳，化归与转化，函数与方程，数与形等知识能力。母题可见于《选修1-1》第四章习题4-1A组第3题。2021/5/9152.认知分析

(条件.结论.难点.关键)

已知条件为给出函数解析式，目标为求该函数的最大值，

隐含条件和潜在信息为：先求出定义域为且有

易错点，易混点，关键点都在定义域和式子的结构。

2021/5/9163、解法探究(思路方法)2021/5/917解法1，函数单调性依题意，函数的的定义域是令显然在内是单调内是单调递减函数，即函数在处取得极值。我们都知道连续函数的最值必

综上，有函数的最大值是故选（C）递增函数，在在极值处或区间端点取得，2021/5/918解法步骤：1、求导;2、令求出相应方程的根;

并判断根两侧的符号;3、求出极值，端点的函数值;4、比较得出最值.求导比较求根求值2021/5/919解法2，平方法点评：平方后化归为二次函数的最值问题2021/5/920解法3，基本不等式点评：应用基本不等式注意：一正，二定，三等.2021/5/921解法4，柯西不等式点评：应用柯西不等式需注意到它的结构2021/5/922解法5，三角代换换元后注意新元的范围点评：2021/5/923解法6，数形结合12021/5/924解法7，数形结合22021/5/925解法8，直线与椭圆相切的充要条件2021/5/926解法9，向量法2021/5/927解法10，公式法2021/5/928解题思想，方法和规律总结解决此题我想到了十种方法，全部属于高中数学中常用的方法，属通性通法，这些方法中涉及到了函数与方程，化归与转化，数形结合，构造函数等数学思想。2021/5/9294.问题拓展(1)、变式该题可以从已知求证变，也可以从隐藏条件，式子结构进行变式。(2)、该题的变式题可以设计出如下一些：变式1：原题：已知函数则它的最大值为()(D)(A)(C)(B)2点评：对已知条件和求解目标进行变式2021/5/930原题：已知函数则它的最大值为()(D)(A)(C)(B)2点评：利用结构进行变式变式2：和=4和=92021/5/931变式3：变式4：求函数的值域。原题：已知函数则它的最大值为()(D)(A)(C)(B)2点评：变3可用单调性解决，变4数形结合最方便2021/5/932：原题：已知函数则它的最大值为()(D)(A)(C)(B)2点评：题型改变但实质一样变式5：2021/5/933结束语

这道简单的模拟题我想到了这十种思路解法和五个变式题，一叶而知秋，我们可想数学世界里有多少这样的“数学美”。所以在我们数学教学的过程中，不能盲目的追求数量不顾质量，采用题海战术，而更应该去教会学生思考，善于思考，进行一道题目多思路解法的训练和变式训练，更能让学生的思维迁移、发散、开拓和活跃，提高学生思维的敏捷性和灵活性，从而提高分析与解答数学题的能力。

2021/5/934结束语数学的世界里并不是缺少美，而是缺少一个善于思考的大脑。如果你热爱数学，请多思考，在数学的世界里“天生我材必有用”；如果你热爱数学，请多思考，在数学的世界里“柳暗花明又一村”；如果你热爱数学，请多思考，在数学的世界里“海阔凭鱼跃，天高任鸟飞”。2021/5/935四、说题案例2导入语(略)2021/5/936问题:（如图1）河边修建一个水泵站，分别向张村、李庄供水，问修在河边什么地方，可使所用的水管最短？

张村李庄水泵站图12021/5/9371.问题背景分析这个问题来自于一个古典名题如图2从A地出发，到笔直的河岸边去饮马，然后再去B地；走什么样的践线最短呢？相传，上面问题是古希腊一位身经百战的将军在作战的时候实际遇到的，将军百思不知其解，于是向居住在亚历山大久负盛名的学者海伦求教。由于这段典故，上述问题成了一个经典名题，后人称为“将军饮马问题”。

B·A·河岸图22021/5/9382.认知分析

“将军饮马”问题，在学生理解方面，存在两大难点，一是如何利用轴对称的性质作出使得线路最短的点。二是说明最短的理由，如何设计探究活动组织有意义的方法和策略，成为了突出重点、突破难点，化难为易的关键，可采用镜面反射的原理创设探究活动，使问题简单化，学生易于理解和掌握。

2021/5/9393.解法探究2021/5/940海伦的解法如下：如图3作B点关于河岸L的对称点B’连结AB’与L相交于C，则C点即为将军所找的饮水点。

具体理由如下：如图4设D是L上其它任意一点（不同于C）由于A，B’，D构成一个三角形，所以AD+DB’＞式AB’①又因为B’是B关于L的对称点所以L垂直平分线段BB’由此得到DB=DB’，CB=CB’进一步得AD+DB’=AD+DBAB’=AC+CB’=AC+CB代入不等式①得：

AD+DB＞AC+CB也就是说在C处饮水所走距离最短到其它位置所走距离都要长。关键:找出B关于直线L的对称点,使问题得以转化.BACB’河岸L图3图4DBACB’河岸L2021/5/941解题思想方法总结利用轴对称思想，将该问题转化为“两点间线段最短”，即“三角形两边之和大于第三边”的问题。将军饮马问题可归结为“求定直线上一动点与直线外两点的距离之和的最小值”问题的数学模型，利用“将军饮马问题”的思想，结合初中的基本几何图形，及直角坐标系中的函数图象等，在解决数学问题发挥着举足轻重的作用。2021/5/9424.问题拓展2021/5/943变式1A、B两村位于一条河的两岸，假定河的两岸笔直且平行，现在要在河上垂直于河岸建一座桥。问：应把桥建在什么位置，才能使由A村经过这座桥到B村的路程最短？（图5）图5图62021/5/944变式2例:若在矩形的球台上，有两个球在M和N的位置上。假如从M打出球，先触及DC边K点，弹出后又触到CB边E点，从CB边再反射出来。问用怎样的打法，才能使这个球反射后正好撞上在N点放置的球？具体做法是：2021/5/945BMDEM’KCANN’2021/5/946变式3变式32021/5/947变式42021/5/948变式42021/5/949求的最小值。初中生