杆系有限元分析矩阵位移法的基本概念课件

第1/2章

杆系有限元分析中的

矩阵位移法第1/2章

杆系有限元分析中的

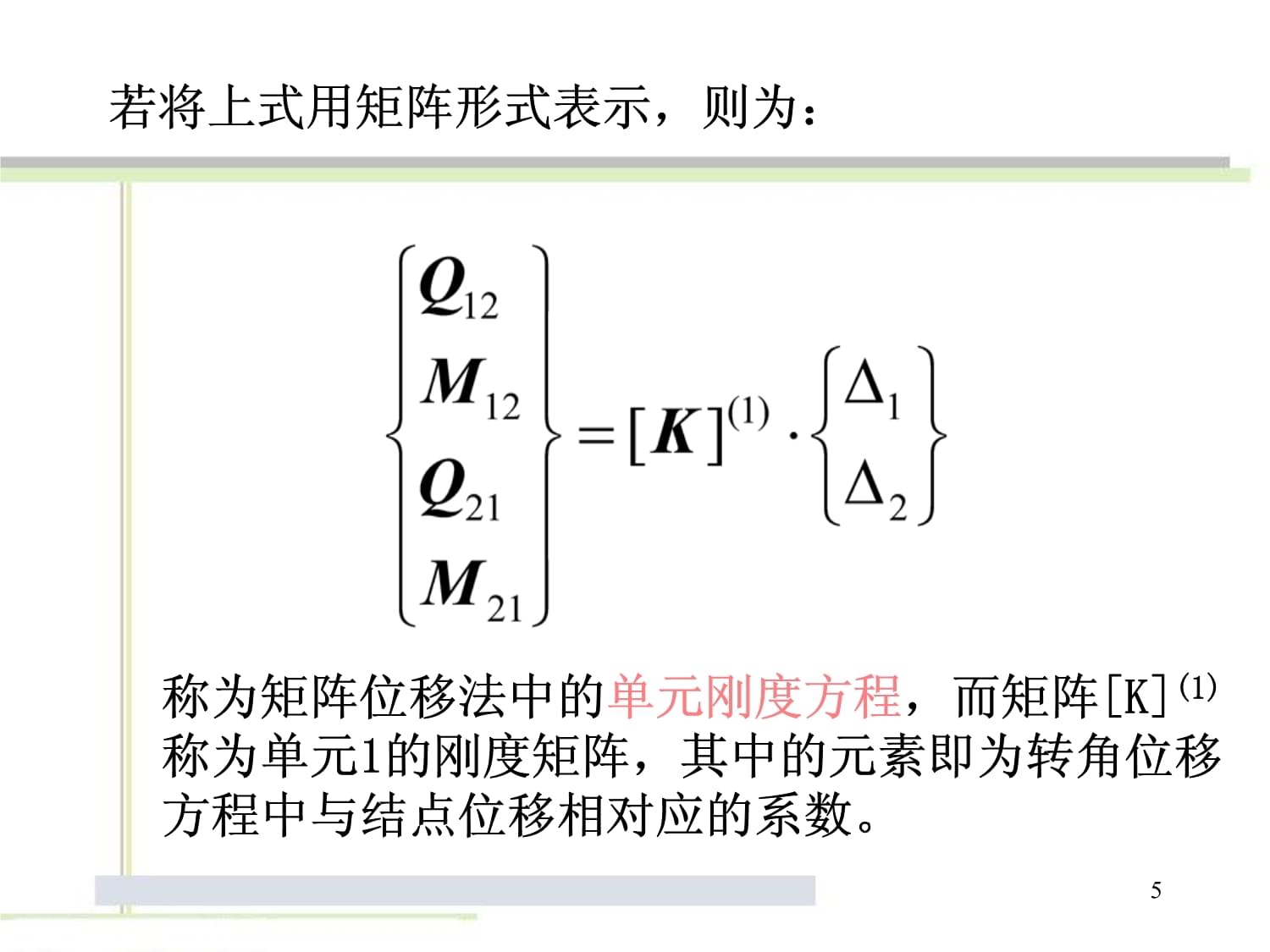
矩阵位移法1例：如图所示平面刚架，忽略杆件轴向变形。例：如图所示平面刚架，忽略杆件轴向变形。2解：1、结构的离散化——将刚架离散为两个单元，如图。解：1、结构的离散化——将刚架离散为两个单元，如图。3确定单元杆端力与杆端位移之间的关系。即分别对单元①、②建立转角位移方程：单元①：2、单元分析确定单元杆端力与杆端位移之间的关系。即分别对单元①、②建立4若将上式用矩阵形式表示，则为：称为矩阵位移法中的单元刚度方程，而矩阵[K](1)称为单元1的刚度矩阵，其中的元素即为转角位移方程中与结点位移相对应的系数。若将上式用矩阵形式表示，则为：称为矩阵位移法中的单元刚度方程5同理单元②：同理单元②：6记做矩阵形式：记做矩阵形式：73、整体分析

根据结点平衡条件和位移协调条件由单元结点的转角位移方程建立位移法的典型方程。即：3、整体分析根据结点平衡条件和位移协调条件由单元结8即：记做矩阵形式：——此即位移法基本方程

即：记做矩阵形式：——此即位移法基本方程9移项整理得：简记做：移项整理得：简记做：10进一步地：此即矩阵位移法的整体刚度方程，也是关于结点位移的线性代数方程组。

[K]为结构整体刚度矩阵}为结构整体结点位移列阵，相当于位移法中的独立结点位移{F}为结构综合结点荷载列阵，{F}＝{FJ}＋{FE}进一步地：此即矩阵位移法的整体刚度方程，也是关于结点位移的线11可见，等式左边相当于在位移法的基本体系中，由结点位移引起的附加约束反力，左边为荷载引起的附加约束反力的负值。其中{FJ}为直接作用在结点上的荷载{FE}为作用在单元上的荷载亦称非结点荷载：产生的附加约束反力的负值，又称为等效结点荷载。显然其等效的意义在于：它与真实的非结点荷载所产生的结点位移相同。可见，等式左边相当于在位移法的基本体系中，由结点位移引起的附124、解结点位移：

5、求杆端内力：

由第4步求得的结点位移，返回单元分析，可确定各单元的杆端内力。6、求结构内力：

运用叠加原理求结构内力。位移法手算时一般采用迭代法求解基本方程，而矩阵位移法除也可采用迭代法（如Gauss消元法）外，常采用更便于计算机运算的三角分解法求解结构整体刚度方程。4、解结点位移：5、求杆端内力：由第4步求得13

由此可见，矩阵位移法的实质和基本步骤与位移法是相同的，只是采取了不同的表达方式，同时，为了便于编程运算，对于结点位移和单元杆端力的方向作了重新规定，以使单元刚度方程（即杆端内力表达式）和整体刚度方程（即位移法典型方程）的形式趋于规范化。1、结构的离散化3、整体分析4、解结点位移5、求杆端内力：6、求结构内力：2、单元分析由此可见，矩阵位移法的实质和基本步骤与位14二、矩阵位移法的步骤1.结构的离散化和数值化；2.单元分析：建立单元刚度方程，即建立单元杆端力与杆端位移关系表达式；3.整体分析：由平衡条件和变形协调条件建立结构总体刚度方程和结构总体刚度矩阵；4.方程求解：求解结点位移；5.计算单元杆端内力。二、矩阵位移法的步骤1.结构的离散化和数值化；2.单元15三、各类线弹性杆元的单元刚度一般平面杆元三、各类线弹性杆元的单元刚度一般平面杆元16不考虑轴向变形的杆元不考虑轴向变形的杆元17只考虑杆端转动的杆元只考虑杆端转动的杆元18平面桁架和空间桁架杆元平面桁架和空间桁架杆元19交叉梁系杆元交叉梁系杆元20杆系有限元分析矩阵位移法的基本概念课件21结构刚度矩阵元素的力学概念和弹性支座的处理结构刚度矩阵元素的力学概念和弹性支座的处理22第1/2章

杆系有限元分析中的

矩阵位移法第1/2章

杆系有限元分析中的

矩阵位移法23例：如图所示平面刚架，忽略杆件轴向变形。例：如图所示平面刚架，忽略杆件轴向变形。24解：1、结构的离散化——将刚架离散为两个单元，如图。解：1、结构的离散化——将刚架离散为两个单元，如图。25确定单元杆端力与杆端位移之间的关系。即分别对单元①、②建立转角位移方程：单元①：2、单元分析确定单元杆端力与杆端位移之间的关系。即分别对单元①、②建立26若将上式用矩阵形式表示，则为：称为矩阵位移法中的单元刚度方程，而矩阵[K](1)称为单元1的刚度矩阵，其中的元素即为转角位移方程中与结点位移相对应的系数。若将上式用矩阵形式表示，则为：称为矩阵位移法中的单元刚度方程27同理单元②：同理单元②：28记做矩阵形式：记做矩阵形式：293、整体分析

根据结点平衡条件和位移协调条件由单元结点的转角位移方程建立位移法的典型方程。即：3、整体分析根据结点平衡条件和位移协调条件由单元结30即：记做矩阵形式：——此即位移法基本方程

即：记做矩阵形式：——此即位移法基本方程31移项整理得：简记做：移项整理得：简记做：32进一步地：此即矩阵位移法的整体刚度方程，也是关于结点位移的线性代数方程组。

[K]为结构整体刚度矩阵}为结构整体结点位移列阵，相当于位移法中的独立结点位移{F}为结构综合结点荷载列阵，{F}＝{FJ}＋{FE}进一步地：此即矩阵位移法的整体刚度方程，也是关于结点位移的线33可见，等式左边相当于在位移法的基本体系中，由结点位移引起的附加约束反力，左边为荷载引起的附加约束反力的负值。其中{FJ}为直接作用在结点上的荷载{FE}为作用在单元上的荷载亦称非结点荷载：产生的附加约束反力的负值，又称为等效结点荷载。显然其等效的意义在于：它与真实的非结点荷载所产生的结点位移相同。可见，等式左边相当于在位移法的基本体系中，由结点位移引起的附344、解结点位移：

5、求杆端内力：

由第4步求得的结点位移，返回单元分析，可确定各单元的杆端内力。6、求结构内力：

运用叠加原理求结构内力。位移法手算时一般采用迭代法求解基本方程，而矩阵位移法除也可采用迭代法（如Gauss消元法）外，常采用更便于计算机运算的三角分解法求解结构整体刚度方程。4、解结点位移：5、求杆端内力：由第4步求得35

由此可见，矩阵位移法的实质和基本步骤与位移法是相同的，只是采取了不同的表达方式，同时，为了便于编程运算，对于结点位移和单元杆端力的方向作了重新规定，以使单元刚度方程（即杆端内力表达式）和整体刚度方程（即位移法典型方程）的形式趋于规范化。1、结构的离散化3、整体分析4、解结点位移5、求杆端内力：6、求结构内力：2、单元分析由此可见，矩阵位移法的实质和基本步骤与位36二、矩阵位移法的步骤1.结构的离散化和数值化；2.单元分析：建立单元刚度方程，即建立单元杆端力与杆端位移关系表达式；3.整体分析：由平衡条件和变形协调条件建立结构总体刚度方程和结构总体刚度矩阵；4.方程求解：求解结点位移；5.计算单元杆端内力。二、矩阵位移法的步骤1.结构的离散化和数值化；2.单元37三、各类线弹性杆元的单元刚度一般平面杆元三、各类线弹性杆元的单元刚度一