非欧几何的产生与发展课件

追寻·溯源追寻·溯源1（1）是古希腊数学家所著的一部数

学著作；

（2）是世界上最著名、最完整且流

传最广的数学著作；

（3）是数学史上的第一座理论丰碑，

最大功绩是确立数学演绎范式。（4）被誉为西方科学的“圣经”。（1）是古希腊数学家所著的一部数

学著作；

（23欧几里得《几何原本》的五条公设：

（1）由任意一点到另外任意一点可以画直线。（2）一条有限直线可以继续延长。（3）以任意点为心及任意的距离可以画圆。（4）凡直角都彼此相等。

（5）同平面内一条直线和另外两条直线相交，若在某一侧的两个内角的和小于二直角的和，则这两条直线经无限延长后在这一侧相交。

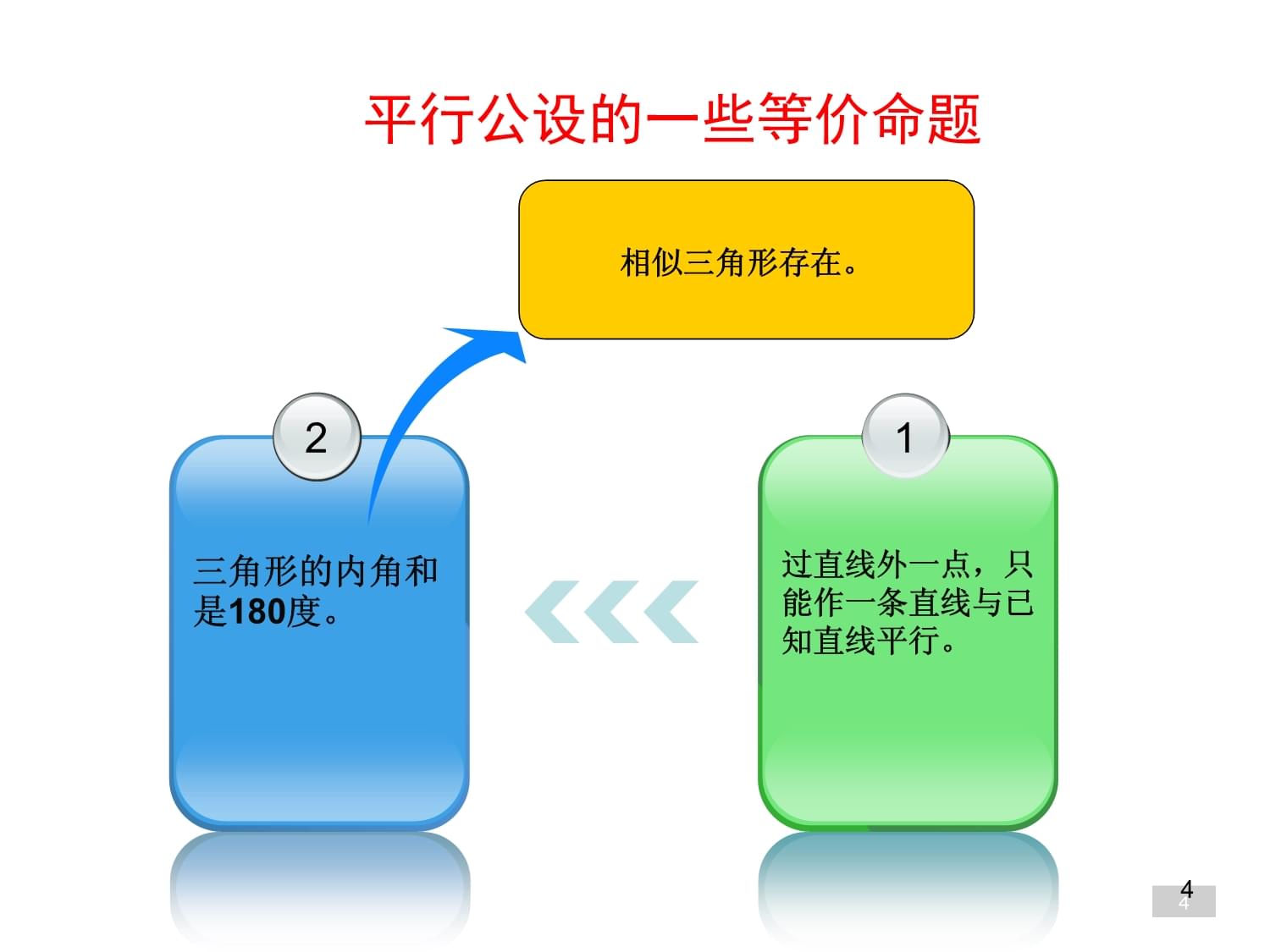
——几何学中的家丑3欧几里得《几何原本》的五条公设：32三角形的内角和是180度。1过直线外一点，只能作一条直线与已知直线平行。平行公设的一些等价命题4相似三角形存在。21平行公设的一些等价命题4相似三角形存在。4萨凯里（意大利）克吕格尔（德国）兰伯特（瑞士）近代数学家一些平行公设研究者托勒密（古希腊）奥马·海亚姆（古阿拉伯）纳西尔·丁（古阿拉伯）古代数学家萨凯里克吕格尔兰伯特近代数学家一些平行公设研究者托勒密奥马·5

三角形的三内角之和小于两个直角？过直线外一点，有无穷多条直线不与该直线相交？怎么可能？？?

萨凯里克吕格尔萨凯里，你没错哦！只是结论似乎与经验不符。平行公设能证明吗？替换平行公设也能展开新的无矛盾的几何学道路吗？

兰伯特三角形的三内角之和小于萨凯里克吕格尔萨凯里，6非欧几何的产生

和发展

非欧几何的产生

和发展7探索·发现探索·发现8非欧几何的诞生高斯罗巴切夫斯基J·鲍耶非欧几何高斯罗巴切夫斯基J·鲍耶910罗氏几何的五条公设：

（1）由任意一点到另外任意一点可以画直线。（2）一条有限直线可以继续延长。（3）以任意点为心及任意的距离可以画圆。（4）凡直角都彼此相等。（5）过直线外的一点至少可以引两条直线与已知直线平行。10罗氏几何的五条公设：10ABCpqDaABCpqDaABCpqDa假设过直线外一点，至少可以引两条直线与已知直线平行。ABCpqDaABCpqDaABCpqDa假设过直线外一点，11（1）三角形内角之和小于两直角，并且内角和是变化的；（2）不存在面积任意大的三角形；（3）同一直线的垂线和斜线不一定相交；（4）如果两个三角形的三个内角相等，它们就全等。

罗氏几何推出的一些结论（1）三角形内角之和小于两直角，并且罗氏几何推出的一些结论12体验·感受体验·感受13C庞加莱罗氏几何模型C庞加莱罗氏几何模型14C过圆内任意两点可以作一条非欧直线段。。一非欧直线可以沿两个方向无限延长。。以非欧平面内任一点为中心，以任意正数长为半径可以作一个非欧圆。凡直角都相等。。罗氏几何五条公设C过圆内任意两点可以作一条非欧直线段。15Cl1l2lABCl1l2lAB163124角非之欧和三小角于形三度内3124角非1718非欧几何的意义：（1）是人类认识史上一个富有创造性的伟大成果，它把人从传统的思想束缚中解放出来，从此，数学认识从以直观为基础的时代进入了以理性为基础的时代，数学表现为人类思维的自由想象。（2）不仅带来了近百年来数学的巨大进步，而且对现代物理学、天文学和人类时空观念的变革都产生深远影响。1913年，物理学家给出了罗氏几何在相对论里的应用；1947年，人们在心理学的研究中，发现视觉空间最好用罗氏几何来描述。

18非欧几何的意义：18传记·感悟传记·感悟19“欧洲数学之王”高斯高斯是当时数学界首屈一指的数学巨匠，负有“欧洲数学之王”的盛名。早在1792年，即罗巴切夫斯基诞生的那一年，他就已经产生了非欧几何思想萌芽，到了1817年已达成熟程度。高斯（德，1777－1855）“欧洲数学之王”高斯高斯是当时数学界首屈一指的数高斯（德，20保守的高斯但是，高斯感到自己的发现与当时流行的康德空间哲学相抵触，担心受到世俗的攻击并激起学术界的不满和社会的反对，因此，他生前一直没敢把自己的这一重大发现公之于世，只是谨慎地把部分成果写在日记和与朋友的往来书信中。他曾在给贝塞尔的一封信中说：如果他公布自己的这些发现，“黄蜂就会围着耳朵飞”，并会“引起波哀提亚人的叫嚣”。保守的高斯但是，高斯感到自己的发现与当时流行的康德空间21进取的J·鲍耶J·鲍耶的父亲是数学教授，也是高斯的朋友。当父亲知道儿子的志趣时，坚决反对并写信责令其停止研究，“它将剥夺你所有的闲暇、健康、思维的平衡以及一生的快乐，这个无底的黑暗将会吞吃掉一千个灯塔般的牛顿。”但小鲍耶仍乐此不疲。鲍耶·亚诺什（匈牙利，1802－1860）进取的J·鲍耶J·鲍耶的父亲是数学教授，也是鲍耶·22懦弱的J·鲍耶1832年2月14日，父亲将小鲍耶的一篇有关非欧几何的论文寄给高斯，请高斯对他儿子的论文发表意见，然而高斯回信说：“称赞他就等于称赞我自己。整篇文章的内容，你儿子所采取的思路和获得的结果，与我在30至35年前的思考不谋而合。”小鲍耶对高斯的答复深感失望。又1840年俄国数学家罗巴切夫斯基关于非欧几何的德文著作出版后，更使小鲍耶灰心丧气，他从此便完全放弃了研究数学。懦弱的J·鲍耶1832年2月14日，父亲将小鲍耶的一篇有关非23创新的罗巴切夫斯基罗巴切夫斯基是从1815年着手研究平行线理论的。1826年2月23日，罗巴切夫斯基于喀山大学物理数学系学术会议上宣读了他的第一篇关于非欧几何的论文《几何学原理及平行线定理严格证明的摘要》，这篇首创性论文的问世，标志着非欧几何的诞生。罗巴切夫斯基（俄国，1792—1856

）创新的罗巴切夫斯基罗巴切夫斯基是从1815年着手罗24刚毅的罗巴切夫斯基此后，罗巴切夫斯基就饱尝“黄蜂绕耳”的滋味：不少权威人物称其学说是“荒唐透顶的伪科学”;有人写匿名信说他是“疯子”;有人用漫画进行讽刺挖苦;德国大诗人歌德的讽刺诗：有几何兮，名曰非欧，自己嘲笑，莫名奇妙！彼得堡科学院院士奥斯特罗格拉茨基：看来，作者旨在写出一部使人不能理解的著作，他达到了自己的目的……由此我得出结论，罗马切夫斯基校长的这部著作谬误连篇，因而不值得科学院的注意。……刚毅的罗巴切夫斯基此后，罗巴切夫斯基就饱尝“黄蜂绕耳25在创立和发展非欧几何的艰难历程上，罗巴切夫斯基始终没能遇到他的公开支持者，就连非欧几何的另一位发现者德国的高斯也不肯公开支持他的工作。1846年，他失去了在喀山大学的所有职务，被迫离开终身热爱的大学工作。但是，罗巴切夫斯基从来没有动摇过对新几何远大前途的坚定信念。直到1855年，在身患重病，卧床不起的困境下，这位双目已失明的老人也没停止对非欧几何的研究，口述发表了他的最后一部巨著《泛几何学》。几何上的哥白尼——罗巴切夫斯基在创立和发展非欧几何的艰难历程上，罗巴切夫几何上的哥白尼——26

19世纪最富有启发性和最值得注意的成就就是非欧几里得几何的发现。

——希尔伯特（德）19世纪最富有启发性和最值得注意的成就27ThankYou!谢谢合作！ThankYou!谢谢合作！28演讲完毕，谢谢观看！演讲完毕，谢谢观看！29追寻·溯源追寻·溯源30（1）是古希腊数学家所著的一部数

学著作；

（2）是世界上最著名、最完整且流

传最广的数学著作；

（3）是数学史上的第一座理论丰碑，

最大功绩是确立数学演绎范式。（4）被誉为西方科学的“圣经”。（1）是古希腊数学家所著的一部数

学著作；

（3132欧几里得《几何原本》的五条公设：

（1）由任意一点到另外任意一点可以画直线。（2）一条有限直线可以继续延长。（3）以任意点为心及任意的距离可以画圆。（4）凡直角都彼此相等。

（5）同平面内一条直线和另外两条直线相交，若在某一侧的两个内角的和小于二直角的和，则这两条直线经无限延长后在这一侧相交。

——几何学中的家丑3欧几里得《几何原本》的五条公设：322三角形的内角和是180度。1过直线外一点，只能作一条直线与已知直线平行。平行公设的一些等价命题33相似三角形存在。21平行公设的一些等价命题4相似三角形存在。33萨凯里（意大利）克吕格尔（德国）兰伯特（瑞士）近代数学家一些平行公设研究者托勒密（古希腊）奥马·海亚姆（古阿拉伯）纳西尔·丁（古阿拉伯）古代数学家萨凯里克吕格尔兰伯特近代数学家一些平行公设研究者托勒密奥马·34

三角形的三内角之和小于两个直角？过直线外一点，有无穷多条直线不与该直线相交？怎么可能？？?

萨凯里克吕格尔萨凯里，你没错哦！只是结论似乎与经验不符。平行公设能证明吗？替换平行公设也能展开新的无矛盾的几何学道路吗？

兰伯特三角形的三内角之和小于萨凯里克吕格尔萨凯里，35非欧几何的产生

和发展

非欧几何的产生

和发展36探索·发现探索·发现37非欧几何的诞生高斯罗巴切夫斯基J·鲍耶非欧几何高斯罗巴切夫斯基J·鲍耶3839罗氏几何的五条公设：

（1）由任意一点到另外任意一点可以画直线。（2）一条有限直线可以继续延长。（3）以任意点为心及任意的距离可以画圆。（4）凡直角都彼此相等。（5）过直线外的一点至少可以引两条直线与已知直线平行。10罗氏几何的五条公设：39ABCpqDaABCpqDaABCpqDa假设过直线外一点，至少可以引两条直线与已知直线平行。ABCpqDaABCpqDaABCpqDa假设过直线外一点，40（1）三角形内角之和小于两直角，并且内角和是变化的；（2）不存在面积任意大的三角形；（3）同一直线的垂线和斜线不一定相交；（4）如果两个三角形的三个内角相等，它们就全等。

罗氏几何推出的一些结论（1）三角形内角之和小于两直角，并且罗氏几何推出的一些结论41体验·感受体验·感受42C庞加莱罗氏几何模型C庞加莱罗氏几何模型43C过圆内任意两点可以作一条非欧直线段。。一非欧直线可以沿两个方向无限延长。。以非欧平面内任一点为中心，以任意正数长为半径可以作一个非欧圆。凡直角都相等。。罗氏几何五条公设C过圆内任意两点可以作一条非欧直线段。44Cl1l2lABCl1l2lAB453124角非之欧和三小角于形三度内3124角非4647非欧几何的意义：（1）是人类认识史上一个富有创造性的伟大成果，它把人从传统的思想束缚中解放出来，从此，数学认识从以直观为基础的时代进入了以理性为基础的时代，数学表现为人类思维的自由想象。（2）不仅带来了近百年来数学的巨大进步，而且对现代物理学、天文学和人类时空观念的变革都产生深远影响。1913年，物理学家给出了罗氏几何在相对论里的应用；1947年，人们在心理学的研究中，发现视觉空间最好用罗氏几何来描述。

18非欧几何的意义：47传记·感悟传记·感悟48“欧洲数学之王”高斯高斯是当时数学界首屈一指的数学巨匠，负有“欧洲数学之王”的盛名。早在1792年，即罗巴切夫斯基诞生的那一年，他就已经产生了非欧几何思想萌芽，到了1817年已达成熟程度。高斯（德，1777－1855）“欧洲数学之王”高斯高斯是当时数学界首屈一指的数高斯（德，49保守的高斯但是，高斯感到自己的发现与当时流行的康德空间哲学相抵触，担心受到世俗的攻击并激起学术界的不满和社会的反对，因此，他生前一直没敢把自己的这一重大发现公之于世，只是谨慎地把部分成果写在日记和与朋友的往来书信中。他曾在给贝塞尔的一封信中说：如果他公布自己的这些发现，“黄蜂就会围着耳朵飞”，并会“引起波哀提亚人的叫嚣”。保守的高斯但是，高斯感到自己的发现与当时流行的康德空间50进取的J·鲍耶J·鲍耶的父亲是数学教授，也是高斯的朋友。当父亲知道儿子的志趣时，坚决反对并写信责令其停止研究，“它将剥夺你所有的闲暇、健康、思维的平衡以及一生的快乐，这个无底的黑暗将会吞吃掉一千个灯塔般的牛顿。”但小鲍耶仍乐此不疲。鲍耶·亚诺什（匈牙利，1802－1860）进取的J·鲍耶J·鲍耶的父亲是数学教授，也是鲍耶·51懦弱的J·鲍耶1832年2月14日，父亲将小鲍耶的一篇有关非欧几何的论文寄给高斯，请高斯对他儿子的论文发表意见，然而高斯回信说：“称赞他就等于称赞我自己。整篇文章的内容，你儿子所采取的思路和获得的结果，与我在30至35年前的思考不谋而合。”小鲍耶对高斯的答复深感失望。又1840年俄国数学家罗巴切夫斯基关于非欧几何的德文著作出版后，更使小鲍耶灰心丧气，他从此便完全放弃了研究数学。懦弱的J·鲍耶1832年2月14日，父亲将小鲍耶的一篇有关非52创新的罗巴切夫斯基罗巴切夫斯基是从1815年着手研究平行线理论的。1826年2月23日，罗巴切夫斯基于喀山大学物理数学系学术会议上宣读了他的第一篇关于非欧几何的论文《几何学原理及平行线定理严格证明的摘要》，这篇首创性论文的问世，标志着非欧几何的诞生。罗巴切夫斯基（俄国，1792—1856

）创新的罗巴切夫斯基罗巴切