2022届江苏省泗阳县实验初级中学高二数学第二学期期末达标检测试题含解析

1、2021-2022高二下数学模拟试卷注意事项1考生要认真填写考场号和座位序号。2试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。3考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。1用数学归纳法证明时，第一步应验证不等式（ ）ABCD2 “m0”是“方程=m表示的曲线为双曲线”的A充分而不必要条件B必要而不充分条件C充分必要条件D既不充分也不必要条件3函数f(x)=ln(ABCD4已知集合，则ABCD5某学习小组

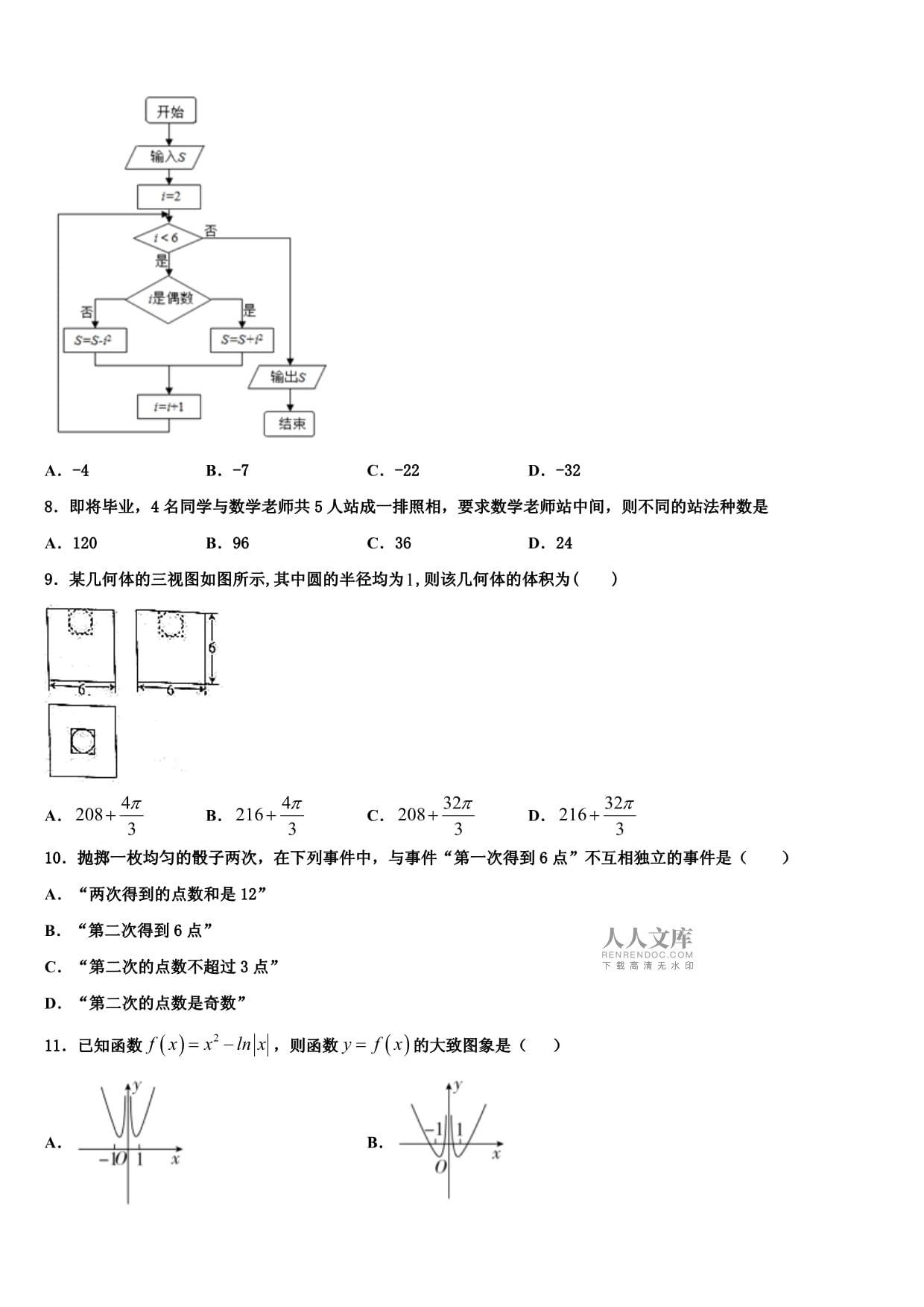
2、有名男生和名女生，现从该小组中先后随机抽取两名同学进行成果展示，则在抽到第个同学是男生的条件下，抽到第个同学也是男生的概率为（ ）ABCD6从区间上任意选取一个实数，则双曲线的离心率大于的概率为（ ）ABCD7执行如图所示的程序框图，若输出的，则输入的（ ）A-4B-7C-22D-328即将毕业，4名同学与数学老师共5人站成一排照相，要求数学老师站中间，则不同的站法种数是A120B96C36D249某几何体的三视图如图所示,其中圆的半径均为,则该几何体的体积为( )ABCD10抛掷一枚均匀的骰子两次，在下列事件中，与事件“第一次得到6点”不互相独立的事件是（ ）A“两次得到的点数和是12”B“

3、第二次得到6点”C“第二次的点数不超过3点”D“第二次的点数是奇数”11已知函数，则函数的大致图象是（ ）ABCD12若满足约束条件则的最大值为A2B6C7D8二、填空题：本题共4小题，每小题5分，共20分。13已知函数，且过原点的直线与曲线相切，若曲线与直线轴围成的封闭区域的面积为，则的值为_14已知关于的实系数方程有一个模为1的虚根，则的取值范围是_15函数f（x）sinx+aex的图象过点（0，2），则曲线yf（x）在（0，2）处的切线方程为_16随机变量，变量，则_三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。17（12分）已知函数，为常数（）若时，已知在定义域内有且只

4、有一个极值点，求的取值范围；（）若，已知，恒成立，求的取值范围。18（12分）某学校高三年级有学生1000名，经调查研究，其中750名同学经常参加体育锻炼（称为类同学），另外250名同学不经常参加体育锻炼（称为类同学），现用分层抽样方法（按类、类分二层）从该年级的学生中共抽查100名同学.（1）测得该年级所抽查的100名同学身高（单位：厘米） 频率分布直方图如图，按照统计学原理，根据频率分布直方图计算这100名学生身高数据的平均数和中位数（单位精确到0.01）；（2）如果以身高达到作为达标的标准，对抽取的100名学生，得到列联表：体育锻炼与身高达标列联表身高达标身高不达标合计积极参加体育锻炼6

5、0不积极参加体育锻炼10合计100完成上表；请问有多大的把握认为体育锻炼与身高达标有关系？参考公式：.参考数据：0.400.250.150.100.050.0250.0100.0050.0010.7081.3232.0722.7063.8415.0246.6357.87910.82819（12分）已知是函数的一个极值点（1）求的值；（2）求函数在上的最大值和最小值20（12分）已知函数，.（1）当 时，求函数图象在点处的切线方程；（2）当时，讨论函数的单调性；（3）是否存在实数，对任意，且有恒成立？若存在，求出的取值范围；若不存在，说明理由.21（12分）如图，在四棱锥中，平面，底面是菱形，分

6、别是棱的中点.（1）证明：平面；（2）求二面角的余弦值.22（10分）已知某厂生产的电子产品的使用寿命（单位：小时）服从正态分布，且，（1）现从该厂随机抽取一件产品，求其使用寿命在的概率；（2）现从该厂随机抽取三件产品，记抽到的三件产品使用寿命在的件数为，求的分布列和数学期望参考答案一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。1、B【解析】根据，第一步应验证的情况，计算得到答案.【详解】因为，故第一步应验证的情况，即.故选：.【点睛】本题考查了数学归纳法，意在考查学生对于数学归纳法的理解和掌握.2、C【解析】根据双曲线的标准方程进行判断

7、【详解】时，方程表示两条直线，时，方程可化为，时表示焦点在轴上的双曲线，时表示焦点在轴上的双曲线故选C【点睛】本题考查双曲线的标准方程，考查充分必要条件，解题关键是掌握双曲线的标准方程3、C【解析】因为fx=lnx2-4x+4x-23=lnx-22x-23，所以函数fx的图象关于点（2,0）对称，4、C【解析】分析：根据集合可直接求解.详解：,故选C点睛：集合题也是每年高考的必考内容，一般以客观题形式出现，一般解决此类问题时要先将参与运算的集合化为最简形式，如果是“离散型”集合可采用Venn图法解决，若是“连续型”集合则可借助不等式进行运算.5、C【解析】设事件A表示“抽到个同学是男生”，事件

8、B表示“抽到的第个同学也是男生”，则，由此利用条件概率计算公式能求出在抽到第个同学是男生的条件下，抽到第个同学也是男生的概率.【详解】设事件A表示“抽到个同学是男生”，事件B表示“抽到的第个同学也是男生”，则，则在抽到第个同学是男生的条件下，抽到第个同学也是男生的概率.故选：C【点睛】本题考查了条件概率的求法、解题的关键是理解题干，并能分析出问题，属于基础题.6、D【解析】分析：求出m的取值范围，利用几何概型的计算公式即可得出.详解：由题意得，解得，即 .故选：D.点睛：几何概型有两个特点：一是无限性；二是等可能性基本事件可以抽象为点，尽管这些点是无限的，但它们所占据的区域都是有限的，因此可用

9、“比例解法”求解几何概型的概率7、A【解析】模拟执行程序，依次写出每次循环得到的S，i的值，当i6时不满足条件i6，退出循环，输出S的值为S+19+162518，从而解得S的值【详解】解：由题意，模拟执行程序，可得i2，满足条件i6，满足条件i是偶数，SS+1，i3满足条件i6，不满足条件i是偶数，SS+19，i1满足条件i6，满足条件i是偶数，SS+19+16，i5满足条件i6，不满足条件i是偶数，SS+19+1625，i6不满足条件i6，退出循环，输出S的值为S+19+162518，故解得：S1故选A点睛：本题主要考查了循环结构的程序框图，模拟执行程序，正确得到循环结束时S的表达式是解题的

10、关键，属于基础题8、D【解析】分析：数学老师位置固定，只需要排学生的位置即可.详解：根据题意得到数学老师位置固定，其他4个学生位置任意，故方法种数有种，即24种.故答案为：D.点睛：解答排列、组合问题的角度：解答排列、组合应用题要从“分析”、“分辨”、“分类”、“分步”的角度入手(1)“分析”就是找出题目的条件、结论，哪些是“元素”，哪些是“位置”；(2)“分辨”就是辨别是排列还是组合，对某些元素的位置有、无限制等；(3)“分类”就是将较复杂的应用题中的元素分成互相排斥的几类，然后逐类解决；(4)“分步”就是把问题化成几个互相联系的步骤，而每一步都是简单的排列、组合问题，然后逐步解决9、A【解

11、析】该几何体为一棱长为6的正方体掏掉一个棱长为2的小正方体，再放置进去一个半径为1的球，所以体积为.故选A.10、A【解析】利用独立事件的概念即可判断【详解】“第二次得到6点”，“第二次的点数不超过3点”，“第二次的点数是奇数”与事件“第一次得到6点”均相互独立，而对于“两次得到的点数和是12”则第一次一定是6点，第二次也是6点，故不是相互独立，故选D【点睛】本题考查了相互独立事件，关键是掌握其概念，属于基础题11、A【解析】根据函数的奇偶性和特殊值进行排除可得结果【详解】由题意，所以函数为偶函数，其图象关于轴对称，排除D；又，所以排除B,C故选A【点睛】已知函数的解析式判断图象的大体形状时，

12、可根据函数的奇偶性，判断图象的对称性：如奇函数在对称的区间上单调性一致，偶函数在对称的区间上单调性相反，这是判断图象时常用的方法之一12、C【解析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，把最优解的坐标代入目标函数得结论.【详解】作出不等式组对应的平面区域如图：（阴影部分），由得，平移直线，由图象可知当直线经过点时，直线在纵轴的截距最大，此时最大，由，解得，代入目标函数得，的最大值为，故选C.【点睛】本题主要考查线性规划中，利用可行域求目标函数的最值，属于简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要

13、注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.二、填空题：本题共4小题，每小题5分，共20分。13、【解析】分析：先根据导数几何意义求切点以及切线方程，再根据定积分求封闭区域的面积，解得的值.详解：设切点，因为，所以所以当时封闭区域的面积为因此，当时，同理可得，即点睛：利用定积分求曲边图形面积时，一定要找准积分上限、下限及被积函数当图形的边界不同时，要分不同情况讨论14、【解析】根据系数方程有虚根,则可得.设方程的虚根为:,则另一个虚根为:,其模为1,可得,即可求得的取值

14、范围.【详解】设方程的虚根为:, 另一个虚根为:由韦达定理可得: 故: 实系数方程有一个模为1的虚根 故 若方程有虚根,则 可得 故答案为: .【点睛】本题考查复数代数形式乘除运算,韦达定理的使用,实系数方程有虚数根的条件,共轭复数的性质、共轭复数的模,意在考查基础知识的掌握与综合应用.15、【解析】先根据求得的值，然后利用导数求得切线的斜率，由此求得切线方程.【详解】由可得，从而， 故在处的切线方程为，即切线方程为.【点睛】本小题主要考查函数解析式的求法，考查在函数图像上一点处切线方程的求法，属于基础题.16、. 【解析】分析：先根据二项分布得,再根据，得详解：因为，所以，因为，所以点睛：二

15、项分布)，则此随机变量的期望可直接利用这种典型分布的期望公式.三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。17、（1）（2）【解析】分析：将代入，求出的表达式，求导，然后综合只有一个极值点即可求出结果法一：将代入，求导后利用单调性来求解；法二：整体思想，采用放缩法进行求解详解：（）当时， 因为在定义域内有且只有一个极值点，所以在内有且仅有一根，则有图知，所以 （），法1： 因，恒成立，则内，先必须递增，即先必须，即先必须，因其对称轴，有图知（此时在 ），所以 法2： 因，所以，所以， 令，因， ，所以递增，所以， 点睛：本题考查了含有参量的导数极值问题和恒成立问题，在解答此类

16、题目时将参数代入，然后根据题意进行转化，结合导数的单调性进行证明，本题有一定难度。 18、（1）174，174.55；（2）列联表见解析；.【解析】（1）根据频率分布直方图的平均数与中位数的公式即可求解；（2）根据频率分布直方图求出身高达标与不达标的比例，结合积极参加体育锻炼和不积极参加体育锻炼的比例，完成表格；根据公式计算出即可下结论.【详解】（1）平均数，前两组频率之和为0.25，前三组频率之和为0.8，所以中位数在第三组中位数为.（2）根据频率分布直方图可得身高不达标所占频率为0.25，达标所占频率为0.75，所以身高不达标25人，达标75人，根据分层抽样抽取的积极参加体育锻炼75人，不

17、积极参加体育锻炼的25人，所以表格为：身高达标身高不达标合计积极参加体育锻炼601575不积极参加体育锻炼151025合计7525100假设体育锻炼与身高达标没有关系.所以有把握认为体育锻炼与身高达标有关系.【点睛】此题考查根据频率分布直方图求平均数和中位数，计算指定组的频率，完成列联表进行独立性检验，关键在于数量掌握相关数据的求解方法，准确计算并下结论.19、（1）（2）最大值为，最小值为【解析】（1）求出，因为是函数的极值点，所以得到求出的值；（2）求出的单调区间研究函数在特定区间上的最值，比较极值点和端点值的大小即判断最值【详解】解：（1）， 是函数的一个极值点，（检验符合） （2）由（

18、1），知 令，得，解之，得，列表如下： 当时，取得极大值；当时，取得极小值而，且函数在上的最大值为，最小值为【点睛】本题考查利用导数研究函数极值和单调性的能力，考查构造函数比较大小，考查学生分析解决问题的能力，属于中档题20、（1）；（2）当， 在上单调递增；当，时， 在，上单调递增，在上单调递减；当时，在，上单调递增，在上单调递减；（3）【解析】分析：（1）求出函数在的导数即可得切线方程；（2），就分类讨论即可；（3）不妨设，则原不等式可以化为，故利用为增函数可得的取值范围详解：（1）当时，所以所求的切线方程为，即（2），当，即时，在上单调递增当，即时，因为或时，；当时，在和上单调递增，在上单调递减；当，即时，因为或时，；当时，在，上单调递增，在上单调递减（3）假设存在这样的实数，满足条件，不妨设，由知，令，则函数在上单调递增所以，即在上恒成立，所以，故存在这样的实，满足题意，其取值范围为点睛：（1）对