信息论第七章

1、信息论第七章第1页，共50页，2022年，5月20日，1点21分，星期一第七章 保真度准则下的信源编码 7.1 失真度和平均失真度 7.2 信息率失真函数及其性质 7.3 二元信源和离散对称信源的 R(D)函数 7.6 连续信源的信息率失真函数7.7 保真度准则下信源编码定理第2页，共50页，2022年，5月20日，1点21分，星期一 总可以找到一种输入分布（信源编码方法），使在无噪无损信道上，能够以信道容量C无误地传输信息。信源编码无噪无损信道R = C ; PE = 0最佳分布消息压缩冗余度最好地利用 C 无噪信道编码定理回顾 第3页，共50页，2022年，5月20日，1点21分，星期一

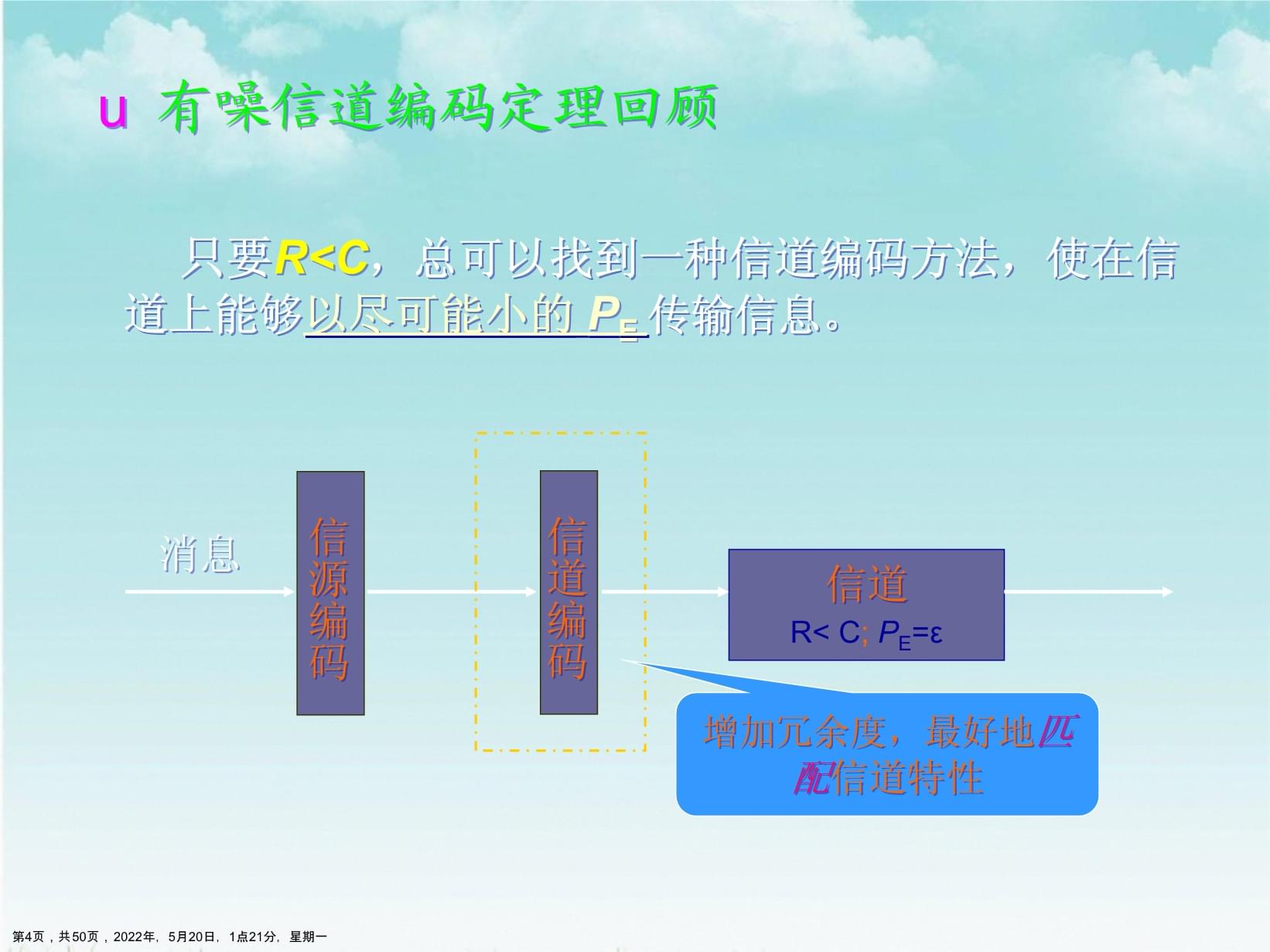
2、只要RC，总可以找到一种信道编码方法，使在信道上能够以尽可能小的 PE 传输信息。 有噪信道编码定理回顾 信源编码消息信道R C; PE=信道编码增加冗余度，最好地匹配信道特性第4页，共50页，2022年，5月20日，1点21分，星期一 对于连续和模拟信源 H(s)= 信道传输率R = H(s)/n（比特/码符号） R = 平均码长 l = Hr(s) = H(s)/logr, l = 实际上,因为Bw有限,C 一定有限,RC, 及l = 均不可能. 存在问题 第5页，共50页，2022年，5月20日，1点21分，星期一 信宿对真实度的要求： 实际语音信号：20Hz8KHz 人耳能够分辨：30

3、0Hz3400Hz 图象色差：可达足够多 视觉分辨：256级（黑白）已足够 实际需求特点 可以允许一定的失真度 完全保真没必要第6页，共50页，2022年，5月20日，1点21分，星期一 限失真的信源编码问题 允许一定的失真度下，能将信源信息压缩到什么程度？（最少需要多少比特才能在收端描述信源？） 一定的信息传输率R下，允许的最大失真是多少？ 引出的研究内容 相关问题 失真如何度量？ 率失真函数如何计算？第7页，共50页，2022年，5月20日，1点21分，星期一7.1 失真度和平均失真度 7.1.1 失真度 7.1.2 平均失真度 保真度准则第8页，共50页，2022年，5月20日，1点21

4、分，星期一7.1.1 失真度 方法抽象：将与讨论重点关系小的部分抽象 涉及信源编码, 对信道进行抽象 信道编码信道信道译码 广义无扰信道* 广义无扰信道*可以略去 信道*是一个没有干扰的广义信道，信宿收到信息的失真只来自于信源编码.第9页，共50页，2022年，5月20日，1点21分，星期一信源编码信道编码信道信道译码信源译码信源信宿广义无扰信道*信源编码信源译码信源信宿第10页，共50页，2022年，5月20日，1点21分，星期一方法虚拟：将讨论重点虚拟细化 将限失真信源的编译码过程虚拟 信源编码广义无扰信道信源译码 试验信道 可以用信道传递概率来描述限失真信 源编译码前后的关系 数据压缩视

5、为消息通过信道, 编码失真 视为信道噪声.7.1.1 失真度 第11页，共50页，2022年，5月20日，1点21分，星期一信源编码信道编码信道信道译码信源译码信源信宿信源编码广义无扰信道*信源译码信源信宿信源信宿试验信道UVP(V|U)第12页，共50页，2022年，5月20日，1点21分，星期一失真度定义信源变量 信源分布经信道传输后, 输出序列 用一个非负函数 d(ui, vj) 表示信源发出符号ui , 接收符号vj的失真度的定量描述.7.1.1 失真度 第13页，共50页，2022年，5月20日，1点21分，星期一失真函数 d(ui, vj) 有rs个, 可排成矩阵形式 失真度定义7

6、.1.1 失真度 第14页，共50页，2022年，5月20日，1点21分，星期一失真函数 d(ui, vj) 有距离的概念 失真度性质性质1： 时, d = 0 性质2：最小距离 d = 0 性质3： 7.1.1 失真度 第15页，共50页，2022年，5月20日，1点21分，星期一 失真函数 d(ui, vj) 可以各式各样, 应尽可能符合信宿的主观特性, 即主观上的失真感觉应与d(ui, vj) 的值相对应. d 越大所感觉的失真也越大, 而且最好成正比. 失真度函数的取值原则7.1.1 失真度 第16页，共50页，2022年，5月20日，1点21分，星期一均方失真： 常用的失真函数适用于

7、连续信源及离散信源, 特别是表示信源输出符号的幅度值.绝对失真： 适用信源同上相对失真： 相对失真与主观特性比较匹配, 但数学处理较繁琐.7.1.1 失真度 第17页，共50页，2022年，5月20日，1点21分，星期一误码失真： 常用的失真函数适用于离散信源.7.1.1 失真度 第18页，共50页，2022年，5月20日，1点21分，星期一例1：离散对称信源(r = s). 信源变量 接收变量 定义单个符号失真度解：失真函数矩阵7.1.1 失真度 第19页，共50页，2022年，5月20日，1点21分，星期一解：失真函数矩阵当再现的接收符号与发送符号相同时, 就不存在失真错误, 所以失真度

8、不同时就有失真存在, 认为引起的失真都相同, 取常数为1. 这种失真称为汉明失真. 汉明失真矩阵D为方阵, 且对角线上的元素为0.7.1.1 失真度 第20页，共50页，2022年，5月20日，1点21分，星期一例2：删除信源(s = r+1). 信源变量 接收变量 定义单个符号失真度解：失真函数矩阵7.1.1 失真度 第21页，共50页，2022年，5月20日，1点21分，星期一解：失真函数矩阵接收符号 作为删除符号. 若把信源符号再现为删除符号 要比再现为其他接收符号的失真程度少一半. 7.1.1 失真度 第22页，共50页，2022年，5月20日，1点21分，星期一 小 结 一般情况下根

9、据实际信源的失真, 可以定义不同的失真和误差; 按主观感觉上的差别大小定义失真度; 可按引起的损失、风险等定义失真度.第23页，共50页，2022年，5月20日，1点21分，星期一7.1.2 平均失真度 定义失真函数的数学期望为平均失真度. 只能表示两个特定的具体符号 与 之间的失真. 为表示信道对信源平均每符号的失真大小, 需要引入平均失真度. 平均失真度第24页，共50页，2022年，5月20日，1点21分，星期一 定义失真函数的数学期望为平均失真度. 平均失真度 是描述某信源在某信道传输(编码)下的失真大小, 是从整体上描述某个系统的失真情况. 7.1.2 平均失真度 第25页，共50页

10、，2022年，5月20日，1点21分，星期一信源序列的平均失真度信源输出符号序列 其中, 随机变量 取自于同一符号集 输入符号序列 共有 个.接收端符号序列 其中, 随机变量 取自于同一符号集 输出符号序列 共有 个.设输入输出7.1.2 平均失真度 第26页，共50页，2022年，5月20日，1点21分，星期一信源序列的平均失真度信源序列的失真度等于序列中对应单个信源符号失真度之和。7.1.2 平均失真度 第27页，共50页，2022年，5月20日，1点21分，星期一N维信源序列的平均失真度7.1.2 平均失真度 第28页，共50页，2022年，5月20日，1点21分，星期一N维信源序列单个

11、符号的平均失真度当信源和信道都无记忆时第l 个分量的平均失真度当离散信源是平稳信源 离散无记忆平稳信源通过无记忆试验信道，序列的平均失真度等于单个符号平均失真度的N倍。7.1.2 平均失真度 第29页，共50页，2022年，5月20日，1点21分，星期一7.1.3 保真度准则 （1）若平均失真度 不大于所允许的失真D，即 ，称此为保真度准则。（2）对于N维信源序列，保真度准则为（3）当信源固定（p(u)给定），单个符号失真度固定（ 给定）时，选择不同的信道，相当于不同的编码方法，所得到的平均失真度 不同。有些信道满足 ，另一些 。把满足D失真许可信道组成一个集合BD， 第30页，共50页，20

12、22年，5月20日，1点21分，星期一7.2 信息率失真函数及其性质 7.2.1 信息率失真函数7.2.2 信息率失真函数的性质 第31页，共50页，2022年，5月20日，1点21分，星期一7.2.1 信息率失真函数 1.已知： 与失真函数 、信源分布 和信道传输函数 有关。当 和 给定后,不同的 将决定了不同的 。 2.在保真度准则条件下： 存在信道满足的集合 。3.信道的互信息 是信道传递函数 的U型凸函数，因此某一信道 使 取极小值4.定义满足失真条件下信源必须传输的最小平均信息量为信息率失真函数，或称率失真函数。第32页，共50页，2022年，5月20日，1点21分，星期一7.2.1

13、 信息率失真函数 离散无记忆平稳信源情况下 物理意义 并不是实际的信道, 而是有失真信源编码或信源压缩的处理. 进而可求出平均互信息的最小值. 即改变编码方法使平均互信息最小, 实质上是选择一种编码方法使信息传输率最小. 是信源特性参数,与试验信道的选择无关. 反映了信源可以压缩的程度,是在满足一定失真度 ( )要求下,信源可压缩的最低值.第33页，共50页，2022年，5月20日，1点21分，星期一7.2.2 信息率失真函数的性质 是D的函数,当D很小时, 应很大。1. 的定义域(0, Dmax)第34页，共50页，2022年，5月20日，1点21分，星期一7.2.2 信息率失真函数的性质

14、是D的函数,当D很小时, 应很大。1. 的定义域(0, Dmax)(3) 由(2)定义得 是使 的全体概率集合。即 和 统计独立。当 时, 此时信源不需要输出任何信息.第35页，共50页，2022年，5月20日，1点21分，星期一7.2.2 信息率失真函数的性质 例 规定失真度为汉明失真度，失真矩阵为求：(1) (2) 达到最小值 时的信道函数？(3)此时的第36页，共50页，2022年，5月20日，1点21分，星期一7.2.2 信息率失真函数的性质 表示为满足保真度准则 ,信道V必须从信源U获取的信息量,即信源必须输出的最小信息率 信源U的率失真函数。第37页，共50页，2022年，5月20

15、日，1点21分，星期一7.2.2 信息率失真函数的性质 例 要求同上例第38页，共50页，2022年，5月20日，1点21分，星期一7.2.2 信息率失真函数的性质 例 要求同上例总结：上面三例中,失真矩阵 每列只有一个最小值,当允许失真度 取最小值 时，信源输出符号数不能有任何的压缩。第39页，共50页，2022年，5月20日，1点21分，星期一7.2.2 信息率失真函数的性质 例 要求同上例三种典型取值信源的信息率可压缩.第40页，共50页，2022年，5月20日，1点21分，星期一7.2.2 信息率失真函数的性质 2. 是关于D的U型凸函数在允许失真度D的定义域内, 是D的U型凸函数.3

16、. 函数的单调递减性和连续性计算 的条件是 ,显然当 时, 将最小。第41页，共50页，2022年，5月20日，1点21分，星期一7.2.2 信息率失真函数的性质 4. 的典型图形 (1) 定义域 (2) U型函数(3) 连续而递减第42页，共50页，2022年，5月20日，1点21分，星期一7.3 二元信源和离散对称信源的R(D)函数 7.3.1 二元对称信源的R(D)函数7.3.2 离散对称信源的R(D)函数第43页，共50页，2022年，5月20日，1点21分，星期一第44页，共50页，2022年，5月20日，1点21分，星期一4-2 根轨迹绘制的基本法则 1. 绘制根轨迹的基本法则 2

17、. 闭环极点的确定. 第45页，共50页，2022年，5月20日，1点21分，星期一1. 绘制根轨迹的基本法则 法则1 根轨迹的起点和终点根轨迹起于开环极点, 终于开环零点. 闭环系统特征方程根轨迹的起点 ,根轨迹的终点 ,开环极点数 = 开环零点数, 数目小的出现在无穷远.第46页，共50页，2022年，5月20日，1点21分，星期一1. 绘制根轨迹的基本法则 法则4 根轨迹在实轴上的分布实轴上的某一区域, 若其右边开环实数零极点个数之和为奇数, 则该区域必是根轨迹. 法则5 根轨迹的分离点与分离角两条或两条以上根轨迹分支在s平面上相遇又立即分开的点, 称为根轨迹的分离点. 根轨迹进入分离点的切线方向与离开分离点的切线方向之间的夹角称为分离角. 分离点坐标 d 和分离角求解公式: 第47页，共50页，2022年，5月20日，1点21分，星期一 小 结 由两个极点(实数极点或复数极点)和一个有限零点组成的开环系统, 只要有限零点没有位于两个实数极点之间, 当K*从0变到时, 闭环根轨迹的复数部