第六章观测误差理论

1、6.1 观测误差观测误差6.2评定精度的标准评定精度的标准6.3观测值函数的中误差观测值函数的中误差6.4等精度观测值的平差等精度观测值的平差6.5误差传播定律在测量中的应用误差传播定律在测量中的应用观测误差测量上一般要求: D往- D返/D0 系统误差系统误差即当直线距离超过一个尺段时，需进行直线定线即当直线距离超过一个尺段时，需进行直线定线. .ABLABSABiABSASBBAABSSibah)(11水准管轴视准轴b1biSA=SB时，hAB=0aa1 总结总结:系统误差具有积累性系统误差具有积累性,可以利用其规律性对可以利用其规律性对观测值观测值进行改正进行改正或者采用一定的或者采用一

2、定的测量方法加以抵消测量方法加以抵消或消弱或消弱.例如：3）、水准仪水准仪i角对测量高差的影响角对测量高差的影响测量误差的分类如如： 1)、距离测量、距离测量010D9.59.4 9.7 9.5 9.6 9.3 9.2 9.6 0.1 -0.2 0 -0.1 0.2 0.3 -0.1 1 2 3 4 5 6 7 N No o测量误差的分类2偶然误差偶然误差 在相同的观测条件下，对某量进行一系列的观测，如在相同的观测条件下，对某量进行一系列的观测，如果观测误差的符号和大小都不一致，表面上没有任何规律果观测误差的符号和大小都不一致，表面上没有任何规律性，这种误差称为偶然误差。性，这种误差称为偶然误

3、差。1.71.61.5 1.591中丝读数： 1.592 1.593例如例如: 2）、）、 读读数误差数误差(水准测量水准测量)例如例如: 3）、）、 照准误差照准误差例如例如: 4）、）、 整平误差整平误差 总结总结: 偶然误差不可避免，通过多余观测，利用数偶然误差不可避免，通过多余观测，利用数理统计理论处理，可以求得参数的最佳估值理统计理论处理，可以求得参数的最佳估值.测量误差的分类 通常，测量中需要进行多余观测。应当剔除观通常，测量中需要进行多余观测。应当剔除观测值中的粗差，利用系统误差的规律性将系统误差测值中的粗差，利用系统误差的规律性将系统误差消除或减弱到可以忽略不计，使观测值主要含

4、有偶消除或减弱到可以忽略不计，使观测值主要含有偶然误差，从而利用数理统计方法求得观测值的最可然误差，从而利用数理统计方法求得观测值的最可靠值。靠值。 总结：总结：在测量工作中，一般需要进行多余观测，在测量工作中，一般需要进行多余观测，发现粗差，将其剔除或重测。发现粗差，将其剔除或重测。测量误差的分类偶然误差偶然误差180lxl观测值与观测值与真值之差真值之差定义：真误差AMPMh时时m分分 偶然误差从表面上看没有任何规律性，但是随着对同一量偶然误差从表面上看没有任何规律性，但是随着对同一量观测次数的增加，大量的偶然误差就表现出一定的统计规律观测次数的增加，大量的偶然误差就表现出一定的统计规律性

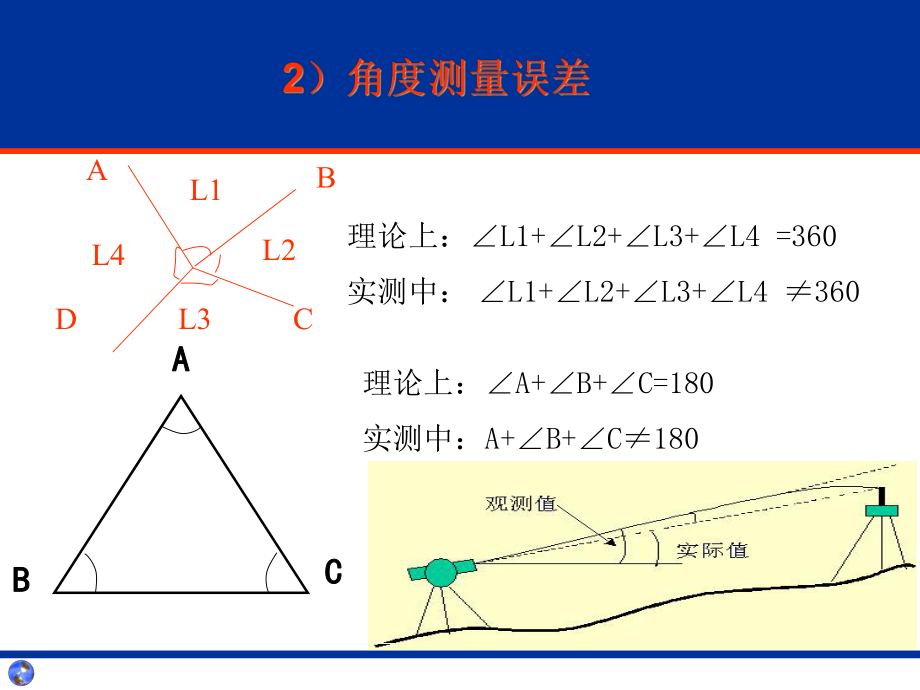
5、，观测次数越多，这种规律性越明显。性，观测次数越多，这种规律性越明显。观测值观测值真值真值观测误差观测误差【例例】在相同的观测条件下，观测了在相同的观测条件下，观测了217217个三角形的全部内角。个三角形的全部内角。n三角形内角和真误差三角形内角和真误差: : A A+B+B+C+C-180-180n i=1,2,3 .217 i=1,2,3 .217 观测误差观测误差F绝对值较小的误差比绝对值较小的误差比绝对值较大的误差个数绝对值较大的误差个数多；多；F绝对值相等的正负误绝对值相等的正负误差的个数大致相等；差的个数大致相等；F最大误差不超过最大误差不超过2727。22221ef21(vi/

6、n)/3误差分布曲线 - 27-24-21-18-15-12 -9 -6 -3 0 3 6 9 12 15 18 21 24 27(vi/n) 每一误差区间上方的长方形面积，每一误差区间上方的长方形面积，代表误差出现在该区间的相对个代表误差出现在该区间的相对个数数直方图1、 愈小， 愈大。 有最大值 )(f当当=0=0时时0)(f时，当横轴是曲线的渐近线，这就是超限数为零、小误差大概率超限数为零、小误差大概率)(f12 2、 是偶函数。 )()(ff)(f对称性对称性曲线有两个拐点，横坐标为： 拐当 愈大时，曲线愈平愈平缓缓，误差分布比较分散分散当 愈小时，曲线愈陡愈陡峭峭，误差分布比较集中集

7、中观测误差观测误差 通过对大量的实验数据进行统计分析后，特别是当观测次数足通过对大量的实验数据进行统计分析后，特别是当观测次数足够多时，可以得出偶然误差具有以下的规律性：够多时，可以得出偶然误差具有以下的规律性：1、在一定的观测条件下，偶然误差的绝对值不会超过一定的限值在一定的观测条件下，偶然误差的绝对值不会超过一定的限值- 超限数为零超限数为零；有限性有限性2、绝对值较小的偶然误差比绝对值大的出现的可能性要大绝对值较小的偶然误差比绝对值大的出现的可能性要大 -小误差大概率小误差大概率：集中性集中性 3、绝对值相等的正负偶然误差出现的可能性相等绝对值相等的正负偶然误差出现的可能性相等 -正负相

8、等正负相等；对称性对称性 4、当观测次数无穷增多时，偶然误差的当观测次数无穷增多时，偶然误差的 算术平均值为零算术平均值为零 -平均理论平均理论 。抵偿性抵偿性lim0nn niin121其中其中观测误差观测误差6.2评定精度的标准评定精度的标准1、中误中误差差: 在相同观测条件下进行一组观测，得出的每个观测值都在相同观测条件下进行一组观测，得出的每个观测值都称为同精度的观测值。即每个观测值的真差不同，但中误称为同精度的观测值。即每个观测值的真差不同，但中误差是相同的。差是相同的。 例：例：2010级的某班的级的某班的3个小组，在相同观测条件下进行四个小组，在相同观测条件下进行四等水准测量。第

9、等水准测量。第1个小组测得闭合差为个小组测得闭合差为+2mm,第第2个小组测得个小组测得闭合差为闭合差为-6mm,第三个小组测得闭合差为第三个小组测得闭合差为0。试判断哪一组观。试判断哪一组观测精度高？测精度高？精度相同精度相同精度精度指的是一组观测值误差分布的指的是一组观测值误差分布的密集密集或或分散分散的程度。的程度。 nm 评定精度的标准评定精度的标准 小，精度高小，精度高 大，精度低大，精度低()f2m2m1m2m1m2m观测条件观测条件误差分布误差分布观测值精度观测值精度 nm 中误差中误差评定精度的标准评定精度的标准2、容许误差（限差）、容许误差（限差）通常取标准差的两倍（或三倍）

10、作为观测值的容许误差。通常取标准差的两倍（或三倍）作为观测值的容许误差。实际中常用中误差代替标准差。即实际中常用中误差代替标准差。即 即大于即大于2倍中误差的真误差，出现倍中误差的真误差，出现的概率为的概率为5%即大于即大于3倍中误差的真误差，出现倍中误差的真误差，出现的概率为的概率为0.3%2221()0 .6 8 32Pfded 954.021)(222222222dedfP997.021)(333323322dedfPm2允m3允或或评定精度的标准评定精度的标准极限作用：区别误差和错误的界线极限作用：区别误差和错误的界线 精度不相同精度不相同3、相对误差、相对误差通常是用来衡量和距离有关

11、的观测量的精度的好坏。通常是用来衡量和距离有关的观测量的精度的好坏。KSmKsSs11 例例:测量两条直线，一条测量两条直线，一条100m，另一条，另一条50m，其，其中误差中误差均为均为10mm试问两条直线的观测精度试问两条直线的观测精度相同吗？哪条直线的观测精度高？相同吗？哪条直线的观测精度高？100m的直线的观测精度高的直线的观测精度高相对中误差，相对真误差和相对极限误差。相对中误差，相对真误差和相对极限误差。评定精度的标准评定精度的标准6.3观测值函数的中误差观测值函数的中误差一一.一般函数的中误差一般函数的中误差对(a)全微分：nndxxFdxxFdxxFdZ2211(b)设有函数：

12、),(21nxxxFZxi为独立独立观测值设 x xi i 有真误差 xixi，函数 Z Z也产生真误差Z Z(a)观测值函数的中误差观测值函数的中误差令 xixi 的系数为 ， (c)式为：iixFf由于xixi 和Z Z是一个很小的量，可代替代替上式中的dxi和 dxz ：nnxxFxxFxxF2211(c)代入(b)得)()(22)(11)()2()2(22)2(11)2() 1 () 1 (22) 1 (11) 1 (knnkkknnnnxfxfxfxfxfxfxfxfxf对对Z观测观测了了k次，次，有有k个式个式(d)观测值函数的中误差观测值函数的中误差对(d)式中的一个式子取平方：

13、（i，j=1n且ij）jijinnxxffxxffxxffxfxfxf2223131212122222221212(e)对K个(e)式取总和：njijijijinnxxffxfxfxf1,222222212122(f)(f)式两边除以K，得(g)式：观测值函数的中误差观测值函数的中误差(g)njijijijinnKxxffKxfKxfKxfK1,222222212122由偶然误差的抵偿性知：0limnxxjin(g)式最后一项极小于前面各项，可忽略不计，前面各项KxfKxfKxfKnn22222221212即即22222221212xnnxxzmfmfmfm(h)观测值函数的中误差观测值函数的

14、中误差则：则：考虑考虑 ，代入上式，得中误差关系式：，代入上式，得中误差关系式：iixFf2222222121nnZmxFmxFmxFm(6-10) 上式为一般函数的中误差公式，上式为一般函数的中误差公式，也称为误差传播定律。也称为误差传播定律。观测值函数的中误差观测值函数的中误差 通过以上误差传播定律的推导，我们通过以上误差传播定律的推导，我们可以总结出可以总结出求观测值函数中误差的步骤求观测值函数中误差的步骤： 1.列出函数式；列出函数式； 2.对函数式求全微分；对函数式求全微分； 3.套用误差传播定律，写出中误差式。套用误差传播定律，写出中误差式。 观测值函数的中误差观测值函数的中误差二

15、二 .几种常用函数的中误差几种常用函数的中误差 1.倍数函数的中误差： 设有函数式 全微分 得中误差式xxZKmmKmKdxdZKxZ22(x为观测值，为观测值，K为为x的系数的系数)观测值函数的中误差观测值函数的中误差例：例：量得1:1000 地形图上两点间长度 l =168.5mm0.2mm, 计算该两点实地距离S及其中误差ms：m2 . 0m5 .168m2 . 0mm2002 . 01000100010001000SmmddlSlSlS解：解：列函数式 求全微分 中误差式观测值函数的中误差观测值函数的中误差2.线性函数的中误差线性函数的中误差 设有函数式 全微分 中误差式nnxkxkx

16、kZ2211nndxkdxkdxkdz22112222222121nnZmkmkmkm观测值函数的中误差观测值函数的中误差例：设有某线性函数例：设有某线性函数 其中其中 x1、x2 、x3分别为独立观测值，它们的中误差分分别为独立观测值，它们的中误差分 别为别为 求Z的中误差mz 。 314121491144xxxZmm6,mm2,mm3321mmm314121491144dxdxdxdzmm6 . 1623214121492144233222211xxxZmfmfmfm解：解：对上式全微分：由中误差式得：观测值函数的中误差观测值函数的中误差 函数式 全微分 中误差式 nnnnnllllx12

17、111lnnlnlnddddx1211121221211222nnnnxmmmm3.算术平均值的中误差式算术平均值的中误差式 观测值函数的中误差观测值函数的中误差由于等精度观测时， ，代入上式： 得mmmmn21nmmnnmX221n 由此可知，算术平均值的中误差比观测值的中误差缩小了缩小了 倍。 对某观测量进行多次观测对某观测量进行多次观测(多余观测多余观测)取平均，取平均， 是提高观测成果精度最有效的方法。是提高观测成果精度最有效的方法。观测值函数的中误差观测值函数的中误差4.和或差函数的中误差和或差函数的中误差 函数式： 全微分： 中误差式：nxxxZ21ndxdxdxdz2122221

18、nZmmmm当等精度观测时： 上式可写成：mmmmmn321nmmZ观测值函数的中误差观测值函数的中误差例：例：测定A、B间的高差 hAB ，共连续测了9站。设测量 每站高差的中误差 m=2mm ，求总高差hAB的中 误差 mh 。 解：解： 921hhhhABmm692nmmh观测值函数的中误差观测值函数的中误差观测值函数中误差公式汇总 观测值函数中误差公式汇总观测值函数中误差公式汇总 函数式 函数的中误差一般函数倍数函数 和差函数 线性函数 算术平均值 ),(21nxxxFZ2222222121nnZmxFmxFmxFmxxZKmmKmKxZ22nxxxZ21nmmZnnxkxkxkZ22

19、112222222121nnZmkmkmkmnnnnnllllx12111nmmX5.4 5.4 等精度直接观测平差等精度直接观测平差 观测值的算术平均值观测值的算术平均值(最或是值) 用观测值的改正数用观测值的改正数v v计算观测值的计算观测值的 中误差中误差 (即:白塞尔公式) 算术平均值的相对中误差算术平均值的相对中误差 等精度直接观测平差等精度直接观测平差 一一. .观测值的观测值的算术平均值算术平均值(最或是值、最可靠值) 证明算术平均值为该量的最或是值： 设该量的真值为设该量的真值为X，则各观测值的真误差为则各观测值的真误差为 1 1= = 1 1- - X X 2 2= = 2

20、2- - X X n= = n- - X X对某未知量未知量进行了n 次观测，得n个观测值1,2,n,则该量的算术平均值为：上式等号两边分别相加得和：上式等号两边分别相加得和： nlnlllLn21 nXl 等精度直接观测平差等精度直接观测平差当观测无限多次时：得Xnlnlim两边除以n：由当观测次数无限多时，观测值的算术平均值就是该 量的真值；当观测次数有限时，观测值的算术平均 值最接近真值。所以，算术平均值是最或是值。L X nXl XLXnln 0)(limlimXLnnn等精度直接观测平差等精度直接观测平差二二. .观测值的改正数观测值的改正数v v ： 以算术平均值以算术平均值为最或

21、是值，并据为最或是值，并据此计算各观测值的此计算各观测值的改正数改正数 v ，符合符合vv=min 的的“最最小二乘原则小二乘原则”。Vi = L - i (i=1,2,n)特点特点1 改正数总和为零：改正数总和为零：对上式取和：以 代入：通常用于计算检核通常用于计算检核L= nv=nL- nv =n -=0v =0特点特点2 vv符合符合“最小二乘原则最小二乘原则”：则即vv=(x-)2=min=2(x-)=0dvv dx(x-)=0nx-=0 x= n等精度直接观测平差等精度直接观测平差 比较前面的公式，可以证明，两式根号内的部分是相等的，比较前面的公式，可以证明，两式根号内的部分是相等的

22、，1nvvnnmnvvm1即在即在 与与 中：中：三三. .精度评定精度评定用观测值的改正数v计算中误差1nvvm一一. .计算公式计算公式( (即白塞尔公式即白塞尔公式) )：等精度直接观测平差等精度直接观测平差1nvvn证明如下：证明如下：nnlLvlLvlLv2211iiiivXLv对上式取对上式取n n项的平方和项的平方和 vvvn22由上两式得由上两式得其中其中: : 0lnLvXlXlXlnn2211等精度直接观测平差等精度直接观测平差改正数改正数真误差真误差 222222)(nnXlnnXnlXLnjijijinn1,2222122122)(02222nn vvnvvvn222n

23、vvnn21nvvn中误差中误差定义定义: :nm白塞尔白塞尔公式公式: :1nvvm等精度直接观测平差等精度直接观测平差解：该水平角真值未知，可用解：该水平角真值未知，可用算术平均值的改正数算术平均值的改正数V V计计 算其中误差：算其中误差：例例1 1：对某水平角等精度观测了5次，观测数据如下表， 求其算术平均值及观测值的中误差。次数观测值VV V备注1764249-4162764240+5253764242+394764246-115764248-39平均764245 V =0VV=60 98 .315601 nVVm4715983 .nmM76 4245 1.74 等精度直接观测平差等

24、精度直接观测平差 例例6-2 某一段距离共丈量了六次，结果如表下所示，求算术某一段距离共丈量了六次，结果如表下所示，求算术平均值、观测中误差、算术平均值的中误差及相对误差。平均值、观测中误差、算术平均值的中误差及相对误差。测测次次 观测值观测值/ m 观测值观测值改正数改正数v/ m m vv 计计 算算 123456平平均均148.643148.590148.610148.624148.654148.647 m628.148 nlL148.628 1 nvvm-15+38+18+4-26-19 0 v 1 nnvvM2251444324166763613046163046 mm7 .24 )

25、16(63046 mm1 .10 DMK m628.148m0101. 0 147161 算例算例3：对某距离用精密量距方法丈量六次，求对某距离用精密量距方法丈量六次，求该距离的算术该距离的算术 平均值平均值 ； 观测值的中误差观测值的中误差 ； 算术平均值的中误算术平均值的中误 差差 ； 算术平均值的相对中误差算术平均值的相对中误差 ：xxmMxM /凡是相对中误差，都必须用分子为1的分数表示。5.5误差传播定律在测量中的应用误差传播定律在测量中的应用 用DJ6经纬仪观测三角形内角时，每个内角观测4个测回取平均，可使得三角形闭合差 m m1515 。例例1：要求三角形最大闭合差m15 ，问用

26、DJ6经纬仪观测三角形每个内角时须用几个测回？ 123=(1+2+3)-180解：解：由题意：2m= 15,则 m= 7.5每个角的测角中误差：测回即43 .45 .8,5 .83 .4,22nnnmmx由于DJ6一测回角度中误差为：由角度测量n测回取平均值的中误差公式：5 .826m3 .435 .7m3 . 4 35 . 7 xm误差传播定律在测量中的应用误差传播定律在测量中的应用例例2 2：试用中误差传播定律分析视距测量的精度。：试用中误差传播定律分析视距测量的精度。 解解:(1):(1)测量水平距离的精度测量水平距离的精度 基本公式：基本公式： 2cosKlD 求全微分：求全微分： dKldlKdDdllDdD)cossin2(cos2水平距离中误差：水平距离中误差： 22222)2sin()cos( mKlmKmlD)206265( 其中：其中： 误差传播定律在测量中的应用误差传播定律在测量中的应用例例2 2：试用中误差传播定律分析视距测量的精度。：试用中误差传播定律分析视距测量的精度。 解解: (2): (2)测量高差的精度测量高差的精度 基本公基本公式： 求全微分：求全微分： dKldlKdDdl