第四节、空间曲线及其方程

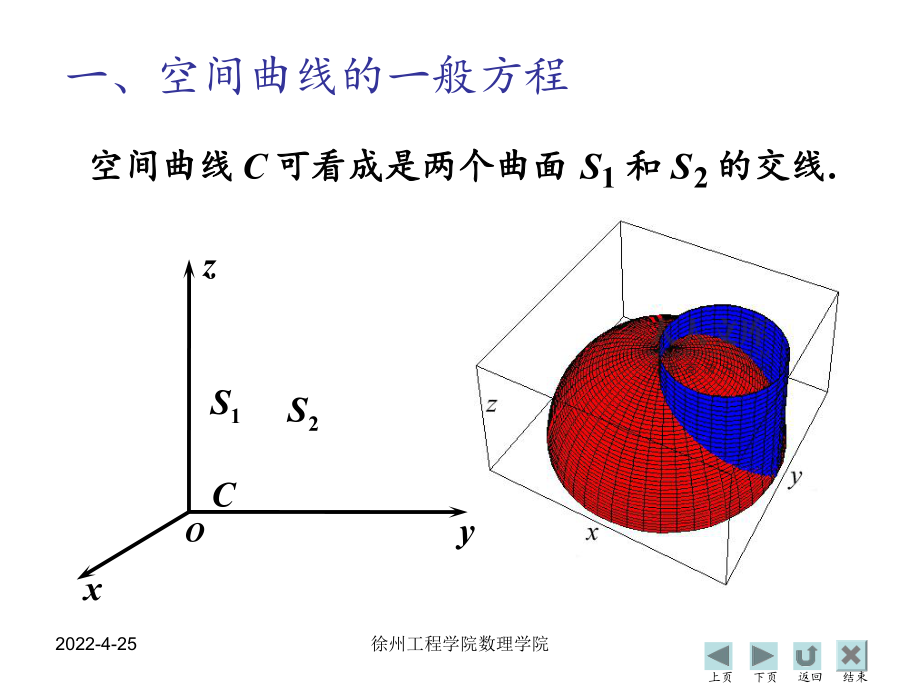
1、上页 下页 返回 结束 2022-4-25徐州工程学院数理学院第四节 空间曲线及其方程一、空间曲线的一般方程一、空间曲线的一般方程二、空间曲线的参数方程二、空间曲线的参数方程三、空间曲线在坐标面上的投影三、空间曲线在坐标面上的投影四、空间曲面或立体在坐标面上的投影四、空间曲面或立体在坐标面上的投影第八章上页 下页 返回 结束 2022-4-25徐州工程学院数理学院. 21的的交交线线和和可可看看成成是是两两个个曲曲面面空空间间曲曲线线SSC一、空间曲线的一般方程xyzO1S2SC上页 下页 返回 结束 2022-4-25徐州工程学院数理学院. , 0),(: , 0),(:21CzyxGSzy

2、xFS它们的交线为它们的交线为为为设两个曲面的方程设两个曲面的方程 . 0),(, 0),( , zyxGzyxFC所以应满足方程组所以应满足方程组的方程的方程标应同时满足两个曲面标应同时满足两个曲面上任何点的坐上任何点的坐因为曲线因为曲线., , ,程组程组所以它的坐标不满足方所以它的坐标不满足方时在两个曲面上时在两个曲面上那么它不可能同那么它不可能同上上不在曲线不在曲线如果点如果点反之反之CM . 0),(, 0),( zyxGzyxFC 的的一一般般方方程程空空间间曲曲线线xyzO1S2SC上页 下页 返回 结束 2022-4-25徐州工程学院数理学院?6332 , 122表示怎样的曲线

3、表示怎样的曲线方程组方程组 zyxyx,632122表示二者的交线表示二者的交线 zxyx 例例1 1 , 122表示圆柱面表示圆柱面因为因为 yx. 6332 表示平面表示平面 zyx解解.为椭圆为椭圆-505x-505y-10-50510z-505x-505y-10-50510z上页 下页 返回 结束 2022-4-25徐州工程学院数理学院?)2()2(,222222表表示示什什么么曲曲线线方方程程组组 ayaxyxaz. ,222的的上上半半球球面面半半径径为为表表示示中中心心在在原原点点ayxaz . 2 , )0 ,2( , )2()2(222的圆周的柱面的圆周的柱面为为半径半径为中

4、心为中心面上以点面上以点准线是准线是轴轴母线平行于母线平行于表示表示aaxOyzayax 例例2 2解解上页 下页 返回 结束 2022-4-25徐州工程学院数理学院: 函数函数的的表示为参数表示为参数、上动点的坐标上动点的坐标如果将如果将tzyxC ).(),(),(tzztyytxx. );,( , 1111上上的的全全部部点点的的变变动动便便可可得得到到曲曲线线随随着着上上的的一一个个点点就就得得到到时时当当给给定定CtzyxCtt 这样的方程组叫做空间曲线的参数方程这样的方程组叫做空间曲线的参数方程 . .二、空间曲线的参数方程二、空间曲线的参数方程上页 下页 返回 结束 2022-4

5、-25徐州工程学院数理学院., ), ( , 222试建立其参数方程试建立其参数方程的轨迹曲线叫螺旋线的轨迹曲线叫螺旋线那么点那么点都是常数都是常数、其中其中轴的正方向上升轴的正方向上升沿平行于沿平行于同时又以线速率同时又以线速率轴旋转轴旋转绕绕角速率角速率上以上以在圆柱面在圆柱面如果空间一点如果空间一点MvzvzayxM , 为参数为参数取时间取时间 t 例例3 3解解, ),( , , )0 , 0 ,( 点点运运动动到到间间时时经经过过出出发发动动点点从从zyxMtaA).0 ,( yxMxOyM 为为面面上上的的投投影影点点在在上页 下页 返回 结束 2022-4-25徐州工程学院数理

6、学院 .,sin,cosvtztaytax 螺旋线的参数方程螺旋线的参数方程, , vbt 记记令令 .,sin,cos .,sin,cos bzayaxvtztaytax上页 下页 返回 结束 2022-4-25徐州工程学院数理学院螺旋线的重要性质螺旋线的重要性质,:00 .:00 bbbz .2 , 2 bh 上上升升的的高高度度时时当当 上升的高度与转上升的高度与转过的角度成正比过的角度成正比. . .2在工程技术上叫做螺距在工程技术上叫做螺距bh 上页 下页 返回 结束 2022-4-25徐州工程学院数理学院 . 0),(, 0),( zyxGzyxF的一般方程为的一般方程为设空间曲线

7、设空间曲线. 0),( yxHz后得到方程后得到方程从方程组中消去变量从方程组中消去变量. , , 所所表表示示的的曲曲面面上上上上的的所所有有点点都都在在由由方方程程这这说说明明曲曲线线必必定定满满足足方方程程、满满足足方方程程组组时时和和、当当 yxzyx三、空间曲线在坐标面上的投影三、空间曲线在坐标面上的投影xyzO 上页 下页 返回 结束 2022-4-25徐州工程学院数理学院. 0),(0),(, 0),( yxHzyxGzyxFz消消去去变变量量. , 0),( 含含曲曲线线这这个个柱柱面面必必定定包包轴轴的的柱柱面面平平行行于于表表示示一一个个母母线线方方程程zyxH. 面面的的

8、投投影影柱柱面面关关于于轴轴的的柱柱面面叫叫做做曲曲线线平平行行于于为为准准线线、母母线线以以曲曲线线xOyz ., 简简称称投投影影面面上上的的投投影影曲曲线线在在面面的的交交线线叫叫做做空空间间曲曲线线投投影影柱柱面面与与xOyxOy xyzO 上页 下页 返回 结束 2022-4-25徐州工程学院数理学院. 0),( 面面的的投投影影柱柱面面关关于于所所表表示示的的柱柱面面必必定定包包含含方方程程xOyyxH . 0, 0),( 面上的投影面上的投影在在曲线必定包含空间曲线曲线必定包含空间曲线所表示的所表示的方程方程xOyzyxH xyzO 上页 下页 返回 结束 2022-4-25徐州

9、工程学院数理学院 面面上上的的投投影影的的曲曲线线方方程程在在包包含含曲曲线线xOz 面面上上的的投投影影的的曲曲线线方方程程在在包包含含曲曲线线yOz . 0, 0),( 0),(, 0),( xzyRzyxGzyxFx消消去去 . 0, 0),(0),(, 0),( yzxTzyxGzyxFy消去消去上页 下页 返回 结束 2022-4-25徐州工程学院数理学院投影曲线的研究过程投影曲线的研究过程空间曲线空间曲线投影柱面投影柱面投影曲线投影曲线上页 下页 返回 结束 2022-4-25徐州工程学院数理学院 . )(3,4: 2222yxzyxz例如曲线例如曲线1 22 yx投影柱面投影柱面

10、 . 0, 122zyx投影曲线投影曲线上页 下页 返回 结束 2022-4-25徐州工程学院数理学院., 1)1()1( , 1222222面上的投影方程面上的投影方程在在求它们的交线求它们的交线已知两球面的方程为已知两球面的方程为xOyCzyxzyx 例例4-1-0.500.51x-1012y-1012z,1,yzz 得到得到从方程组中消去从方程组中消去解解方程得方程得再代入其中任意一个再代入其中任意一个. 02222 yyx上页 下页 返回 结束 2022-4-25徐州工程学院数理学院,程程面面的的投投影影柱柱面面方方关关于于这这就就是是交交线线xOyC . 0, 02222zyyxxO

11、y面面上上的的投投影影方方程程为为于于是是两两球球面面的的交交线线在在-1-0.500.51x-1012y-1012z-1-0.500.51x00.250.50.751y-0.1-0.0500.050.1z上页 下页 返回 结束 2022-4-25徐州工程学院数理学院.211222在坐标面上的投影在坐标面上的投影求曲线求曲线 zzyx43 )1(22 yxz后得后得消去变量消去变量-1-0.500.51x-1-0.500.51y-1-0.500.51z-1-0.500.51x . 0,4322zyxxOy面上的投影为圆周面上的投影为圆周在在 例例5 5解解,21)2(上上的的圆圆周周空空间间曲

12、曲线线为为平平面面 z.23 , 0,21 xyzxOz面面上上的的投投影影为为线线段段所所以以在在上页 下页 返回 结束 2022-4-25徐州工程学院数理学院面上的投影也为线段面上的投影也为线段在在 yOz)3(.23 , 0,21 yxz上页 下页 返回 结束 2022-4-25徐州工程学院数理学院四、空间曲面或立体在坐标面上的投影四、空间曲面或立体在坐标面上的投影. , )(3 4 2222面上的投影面上的投影求它在求它在所围成所围成面面和锥和锥一个立体由上半球面一个立体由上半球面xOyyxzyxz 半半球球面面和和锥锥面面的的交交线线为为 例例6解解 . )(3,4: 2222yxzyxz. 122 yxz 得得投投影影柱柱面面消消去去上页 下页 返回 结束 2022-4-25徐州工程学院数理学院 . 0, 1 22zyxxOy面面上上的的投投影影是是在在面上的投影区域是面上的投影区域是立体在立体在 xOy . 0, 122zyx上页 下页 返回 结束 2022-4-25徐州工程学院数理学院在在各各坐坐标标面面上上的的投投影影椭椭圆圆抛抛物物面面zyx222