



版权说明:本文档由用户提供并上传,收益归属内容提供方,若内容存在侵权,请进行举报或认领
文档简介
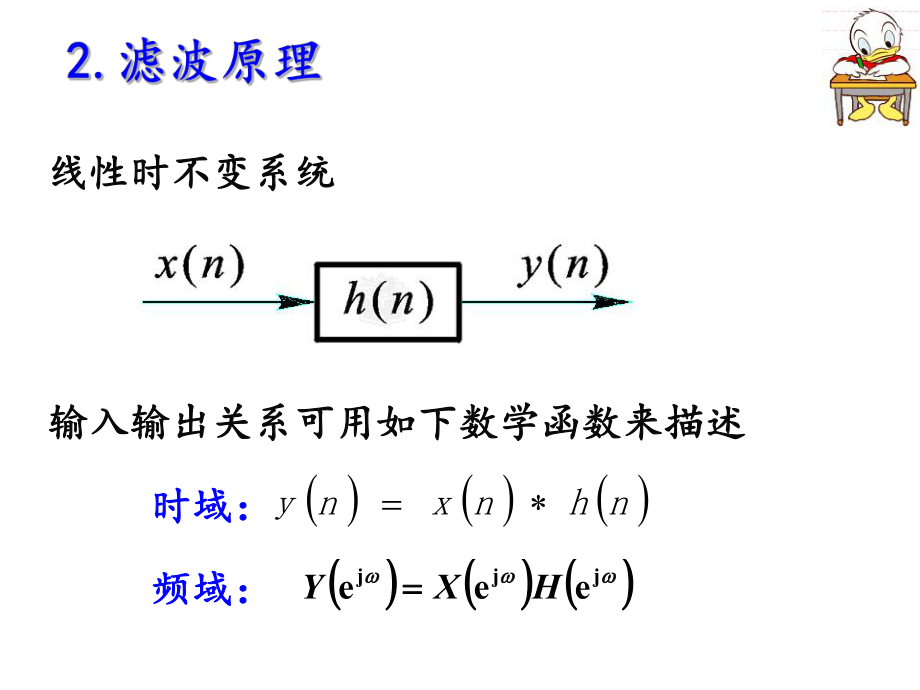
1、葛青葛青4.14.1滤波器的概念及分类滤波器的概念及分类l数字滤波器:数字滤波器:通过对数字信号的运算处理,改变信号频谱,完成滤波作用的算法或装置。数字滤波器具有稳定、适应性强、线性相位等优点,避免了模拟滤波器固有的电压漂移、温度漂移和噪声等问题。线性时不变系统线性时不变系统输入输出关系可用如下数学函数来描述输入输出关系可用如下数学函数来描述 时域:时域: 频域:频域: nhnxny jjjeeeHXY l幅频特性:表示信号通过该滤波器后各频幅频特性:表示信号通过该滤波器后各频率成分的衰减情况率成分的衰减情况l相频特性:反映各频率成分通过滤波器后相频特性:反映各频率成分通过滤波器后在时间上的延
2、时情况(在时间上的延时情况( 联系无失真传输条联系无失真传输条件)件))()()(jeHH假定假定 和和 如图(如图(a)、()、(b)所示,则由上式)所示,则由上式可得出可得出 的波形如图(的波形如图(c)所示。)所示。滤波原理滤波原理 jeX jeH jeY滤波后,输出滤波后,输出 频率成分中频率成分中 的部分被滤除掉了。的部分被滤除掉了。设计不同形状的设计不同形状的 ,就可以得到不同的滤波结果。,就可以得到不同的滤波结果。c jeHl滤波器的设计就是用一个因果稳定的线性移不变系统的系统函数去逼近理想滤波器的性能。l数字滤波器设计数字滤波器设计: :确定传输函数H(z)的过程。l表征滤波器
3、频率响应的特征参量(表征滤波器频率响应的特征参量(3个参量)个参量)(1 1)幅度平方响应:幅度的平方与频率的关系)幅度平方响应:幅度的平方与频率的关系(2 2)相位响应)相位响应(3 3)群延迟响应)群延迟响应(物理意义):相位对角频率的导数的负值。若滤波器通带内群延迟响应=常数,则为线性相位滤波器,联系无失真传输问题。无失真传输系统无失真传输系统 如果系统响应仅是输入信号在时间上的延时和幅度上的放大或缩小,就认为信号在传输过程中没有失真,这种系统称为无失真传输系统无失真传输系统。无失真传输系统( )f t0( )()y tKf tt( )h t0( )()h tKtt0( )j tHKe(
4、 )HK无失真传输系统0)(t分类标准分类标准可分类型可分类型处理信号的方式处理信号的方式经典滤波器和现代滤波器经典滤波器和现代滤波器处理信号的类型处理信号的类型模拟滤波器和数字滤波器模拟滤波器和数字滤波器通过信号的频段通过信号的频段低通、高通、带通和带阻滤波器低通、高通、带通和带阻滤波器实现方法实现方法模拟滤波器模拟滤波器数字滤波器数字滤波器LC滤波器、螺旋滤波器、晶体滤滤波器、螺旋滤波器、晶体滤波器、陶瓷滤波器、声表面滤波波器、陶瓷滤波器、声表面滤波器、微带滤波器和有源滤波器等器、微带滤波器和有源滤波器等有限冲激响应滤波器有限冲激响应滤波器无限冲激响应滤波器无限冲激响应滤波器设计方法设计方
5、法Butterworth滤波器、滤波器、Chebyshev滤波器和椭圆滤波器等滤波器和椭圆滤波器等l经典滤波器:用于提取有用的信号,抑经典滤波器:用于提取有用的信号,抑制不需要的干扰;或将信号分成不同的制不需要的干扰;或将信号分成不同的频率成分;频率成分;l现代滤波:信号检测和信号估计现代滤波:信号检测和信号估计经典滤波器和现代滤波器经典滤波器和现代滤波器 模拟滤波器幅频特性曲线模拟滤波器幅频特性曲线数字滤波器幅频特性曲线数字滤波器幅频特性曲线低通滤波器(LPAF/LPDF):Low pass filter带通滤波器(BPAF/BPDF):Bandpass filter高通滤波器(HPAF/H
6、PDF):High pass filter带阻滤波器(BSAF/BSDF):Bandstop filter模拟(Analog)滤波器:是用来处理模拟信号的处理系统。数字(Digital)滤波器:是用来处理数字信号的处理系统。x(n)y(n)数字信号处理?IIR(infinite impulse response):IIR(infinite impulse response):有限冲激响应滤波器有限冲激响应滤波器, ,单位冲激响应单位冲激响应h(n)h(n)是无限是无限长序列长序列 FIR(finite impulse response): FIR(finite impulse response
7、):无限冲激响应滤波器无限冲激响应滤波器, ,单位冲激响应单位冲激响应h(n)h(n)是有限是有限长序列长序列x(n)y(n)数字信号处理?4.IIR系统与系统与FIR系统系统l从系统的单位采样响应来区分1.无限长单位冲激响应(IIR)系统:单位冲激响应h(n)是无限长序列2.有限长单位冲激响应(FIR)系统:单位冲激响应h(n)是有限长序列x(n)y(n)数字信号处理?五、五、IIRIIR系统与系统与FIRFIR系统系统l从系统函数的构造来区分1.IIR系统:至少有一个极点。包括全极点系统(分子只有常数项)和零极点系统(分子不止常数项);有反馈环路,采用递归型结构。2.FIR系统:收敛域内无
8、极点,是全零点系统。无反馈环路,多采用非递归结构。0001( )1MMmmmmmmNNkkkkkkb zb zH za za zx(n)y(n)数字信号处理?IIR系统与系统与FIR系统系统l从系统函数的构造来区分从系统函数的构造来区分11101)(数为:离散因果系统的传递函MiiiNiiizbzazHx(n)y(n)数字信号处理?IIR系统与系统与FIR系统系统)1N-(.)2-()1-()()(.)(,则0全为若)1(1210)1(-12-21-1010nananananhzazazaazazHbNNNNiiii当0nN-1时,h(n)=0具有这种形式的滤波器称为具有这种形式的滤波器称为F
9、IR滤波器滤波器(Finite Impulse Response)。其差分方程为:。其差分方程为:)1N-(.)1-()()(110nfanfanfanyNx(n)y(n)数字信号处理?(2)bi(2)bi中至少有一项不为零,并且分母中至少有中至少有一项不为零,并且分母中至少有一个根不为分子所抵消一个根不为分子所抵消.)2-()1-()()(1.),1(1)(021010nnnanhzzzazazH具有这种形式的滤波器称为具有这种形式的滤波器称为IIR滤波器滤波器(Infinite Impulse Response)。其差分方程为:。其差分方程为:x(n)y(n)数字信号处理?IIR系统与系统
10、与FIR系统系统1.IIR系统:至少有一个极点。包括全极点系统(分子只有常数项)和零极点系统(分子不止常数项);有反馈环路,采用递归型结构。2.FIR系统:收敛域内无极点,是全零点系统。无反馈环路,多采用非递归结构。数字滤波器的性能要求l一个理想滤波器,要求所在通频带内幅频响一个理想滤波器,要求所在通频带内幅频响应是一常数;相位频率相应为零或是频率的应是一常数;相位频率相应为零或是频率的线性函数。但一个实际的滤波器要是不可能线性函数。但一个实际的滤波器要是不可能得到上述幅频和相频响应。以低通滤波器为得到上述幅频和相频响应。以低通滤波器为例,频率响应有通带、过渡带及阻带三个范例,频率响应有通带、
11、过渡带及阻带三个范围围。数字滤波器的性能要求p p:通带衰减通带衰减 s s:阻带衰减阻带衰减 p p:通带截止频率通带截止频率s s:阻带截止频率阻带截止频率p p-s s :过渡带过渡带 通带允许的最大衰减通带允许的最大衰减 阻带最小衰减:阻带最小衰减: ps pccHHH1lg20elg20eelg20jj0jpsHHHlg20elg20eelg20ssjj0js数字滤波器的性能要求式中假定式中假定 被归一化为被归一化为1 11e0jHl按设计任务,确定滤波器性能要求,制定技按设计任务,确定滤波器性能要求,制定技术指标术指标l一个因果稳定的离散一个因果稳定的离散LSILSI系统的系统函数
12、系统的系统函数H H( (z z) )逼近此性能指标逼近此性能指标l利用有限精度算法实现此系统函数:如运算利用有限精度算法实现此系统函数:如运算结构、字长的选择等结构、字长的选择等l实际技术实现:软件法、硬件法或实际技术实现:软件法、硬件法或DSPDSP芯片芯片法法数字滤波器的设计过程数字滤波器的设计过程数字滤波器的设计数字滤波器的设计lIIRIIR滤波器设计主要内容包括:滤波器设计主要内容包括:巴特沃思、切比雪夫模拟低通滤波器设计;巴特沃思、切比雪夫模拟低通滤波器设计;脉冲响应不变法和双线性变换法的数字化变脉冲响应不变法和双线性变换法的数字化变换方法;换方法;数字高通、带通和带阻滤波器的设计
13、。数字高通、带通和带阻滤波器的设计。l而而FIRFIR滤波器是直接采用的数字式设计方法。滤波器是直接采用的数字式设计方法。针对针对FIRFIR滤波器特征,首先介绍了其线性相滤波器特征,首先介绍了其线性相位的实现条件,然后介绍了窗函数法和频率位的实现条件,然后介绍了窗函数法和频率抽样法的设计方法。抽样法的设计方法。 设计设计IIRIIR数字滤波器一般有以下两种方法:数字滤波器一般有以下两种方法:l1. 1. 模拟滤波器模拟滤波器: :首先设计一个合适的模拟滤首先设计一个合适的模拟滤波器,然后将它转换成满足给定指标的数字波器,然后将它转换成满足给定指标的数字滤波器,这种方法适合于设计幅频特性比较滤
14、波器,这种方法适合于设计幅频特性比较规则的滤波器,例如低通、高通、带通、带规则的滤波器,例如低通、高通、带通、带阻等阻等。l2.直接在频域或者时域中进行数字滤波器设直接在频域或者时域中进行数字滤波器设计,由于要联立方程,设计时需要计算机作计,由于要联立方程,设计时需要计算机作辅助设计。辅助设计。4.2 IIR数字滤波器的设计数字滤波器的设计l IIR滤波器以模拟低通滤波器为基础的设计方滤波器以模拟低通滤波器为基础的设计方法,为了设计其他的选频滤波器(高通,带通法,为了设计其他的选频滤波器(高通,带通,带阻等),需要对低通滤波器进行频率转换,带阻等),需要对低通滤波器进行频率转换,在设计过程中有
15、两种不同的变换,在设计过程中有两种不同的变换,频带变换和频带变换和模拟模拟/数字变换。根据这两种变换的先后次序,数字变换。根据这两种变换的先后次序,引出两种设计方法引出两种设计方法。 4.2 IIR数字滤波器的设计数字滤波器的设计归一化归一化模拟低通模拟低通模拟高通、模拟高通、带通、带阻带通、带阻数字高通、数字高通、带通、带阻带通、带阻模拟域模拟域频带变换频带变换双线性双线性变换变换归一化归一化模拟低通模拟低通数字数字低通低通数字高通、数字高通、带通、带阻带通、带阻数字域数字域频带变换频带变换或双线性或双线性变换变换冲激响应冲激响应不变法不变法其它非低通数字滤波器的设计过程其它非低通数字滤波器
16、的设计过程IIRIIR的设计方法的设计方法借用模拟滤波器借用模拟滤波器先设计一个合适的模拟滤波器,然后变换成先设计一个合适的模拟滤波器,然后变换成满足给定指标的数字滤波器。满足给定指标的数字滤波器。设计步骤设计步骤 将给定的数字滤波器的技术指标转换为模拟滤将给定的数字滤波器的技术指标转换为模拟滤 波器的技术指标;波器的技术指标;根据转换后的技术指标设计模拟原型滤波器;根据转换后的技术指标设计模拟原型滤波器; 按照一定规则将模拟滤波器转换为数字滤波器。按照一定规则将模拟滤波器转换为数字滤波器。常用模拟低通滤波器及其特点1.巴特沃思巴特沃思(Butterworth)(Butterworth)滤波器
17、滤波器: 特点是从通带中心向两边幅频特性单调下降;2.2.切比雪夫型切比雪夫型I(Chebyshev)滤波器:通带内有等波纹幅频特性函数,阻带内有单调下降的幅频特性函数;3.3.切比雪夫型切比雪夫型II(Chebyshev)滤波器:通带内有单调下降的幅频特性函数,阻带内有等波纹幅频特性函数;4. .椭圆椭圆滤波器(又称考尔Cauer滤波器或双切比雪夫切比雪夫滤波器):通带和阻带内均有等波纹幅频特性;5.贝塞尔贝塞尔(Bessel)(Bessel)滤波器滤波器(又称最大平坦群时延滤波器):在中心频率附近逼近线性相位特性;模拟滤波器的设计过程模拟滤波器的设计过程(1)根据要求确定设计指标;(2)选
18、择滤波器类型;(3)计算滤波器阶数;(4)通过查表或计算确定滤波器的系统 函数Ha(s);(5)综合实现并装配调试;1.巴特沃思低通滤波器(1)基本性质 巴特沃思滤波器以巴特沃思函数来近似滤波器的系统函数。巴特沃斯滤波器是根据幅频特性在通频带内具有最平坦特性定义的滤波器。 221()1()aNcHj N N为滤波器阶数为滤波器阶数c c为为3dB3dB截止频率截止频率巴特沃思滤波器的低通模平方函数表示巴特沃思滤波器的低通模平方函数表示巴特沃思低通滤波平方幅频特性函数巴特沃思低通滤波平方幅频特性函数巴特沃斯滤波器的主要特征 a.对所有的N: 即即1)(20jHa21)(2cjHa707. 0)(
19、cjHadBjHca3)(lg20b. 是 的单调下降函数。c. 随着阶次N的增大而更接近于理想低通滤波器。2)( jHa2)( jHa 归一化原型滤波器是指截止频率归一化原型滤波器是指截止频率 已经归一已经归一化成化成 的低通滤波器。对于截止频率为的低通滤波器。对于截止频率为 某个低通滤波器,则令某个低通滤波器,则令 替归一化原型滤波器系替归一化原型滤波器系统函数中的统函数中的 , 对于其他高通、带通、带阻滤波器,可应用后面对于其他高通、带通、带阻滤波器,可应用后面讨论到的频带变换法,由其变换得出。讨论到的频带变换法,由其变换得出。 c1ccscscss/巴特沃斯低通滤波器的幅度平方函数为:
20、巴特沃斯低通滤波器的幅度平方函数为:NcajH22)(11|)(|N为滤波器的阶次, 为3dB截频。c( (2 2) )巴特沃思低通滤波器巴特沃思低通滤波器设计过程设计过程通带最大衰减和阻带最小衰减可由定义式求出通带最大衰减和阻带最小衰减可由定义式求出: :( (设设=0=0处幅度归一化到处幅度归一化到1 1) ), , 则则: :22| )(|lg10| )(|lg10saspapjHjHNcajH22)(11|)(|(2)巴特沃思低通滤波器设计过程1)1)求出求出N N10/210)(1pNcp10/210)(1sNcs110110)(10/10/spNspN Nminmin应取向上取整。
21、应取向上取整。2 2) )如技术指标未给出如技术指标未给出 ,则可由下式计算:,则可由下式计算: 或或采用上式求采用上式求 ,阻带指标有富裕量;,阻带指标有富裕量;下式则通带指标有富裕量。下式则通带指标有富裕量。cNpcp211.0)110(Nscs211.0)110(c查表求得归一化传输函数 ,令 代替归一化原型滤波器系统函数中的 , 即得到实际滤波器传输函数Ha(s)。3)求系统函数Ha(s)(sHacss/s低通巴特沃斯滤波器设计步骤:低通巴特沃斯滤波器设计步骤:(1 1)由)由 求滤波器阶次求滤波器阶次N N;(2 2)由)由N N查表,求出归一化传输函数查表,求出归一化传输函数 ;(
22、3 3)令)令 代入代入 ,得实际,得实际 滤波器传输函数滤波器传输函数H Ha a(s) (s) 。 sspp和、css/)(sHa)(sHaN Nminmin应取向上取整。应取向上取整。Npcp211.0)110(Nscs211.0)110(N及 计算c或 2dB1lg101 ApNcajH22)(11|)(| nH22211 nA2ps2psdBs1lg10 110p1 . 02 ps1 . 01 . 0/lg110/110lgps n通带边频: 通带的最大衰减为: 阻带边频为: 阻带的最小衰减为: dBp2例:设计一巴特沃思低通滤波器,使其满足以下指标: sradp/20srads/3
23、0dBS10解:根据滤波器技术指标 取N=4, 查表得四阶巴特沃思多项式,得归一化系统函数表达式确定阶次N371. 3N1613. 2414. 3613. 21)(234sssssHa巴特沃斯归一化低通滤波器参数巴特沃斯归一化低通滤波器参数巴特沃斯归一化低通滤波器参数巴特沃斯归一化低通滤波器参数巴特沃斯归一化低通滤波器参数巴特沃斯归一化低通滤波器参数Npcp211.0)110(代入代入387.21ccss1613. 2414. 3613. 21)(234sssssHa54233451009. 210556. 210562. 188.551009. 2)(sssssHa1.巴特沃思滤波器设计步骤
24、:巴特沃思滤波器设计步骤:(1)(1)根据技术指标求根据技术指标求求出滤波器的阶数N和3dB截止频率cpspsNpcp211.0)110(Nscs211.0)110(N Nminmin应取向上取整。应取向上取整。或或1.1.巴特沃思滤波器设计步骤:巴特沃思滤波器设计步骤:(2)(2)求系统函数求系统函数H Ha a(s)(s) 1)1)查表求查表求 H Ha a(s)(s) 查表求得归一化传输函数查表求得归一化传输函数 ,令 代替归一化原型滤波器系统函数中的 , 得到实际滤波器传输函数。cs)(sHas 求滤波器的极点,并由求滤波器的极点,并由s s平面左半平面的平面左半平面的极点构成极点构成
25、 。幅度平方函数极点为: 将s平面左半平面的N个极点分配给1 2122 0,1,2,21kjNkcsekN)()(10kNkNcasssH)(sHa)(sHa2)2)极点法求系统函数极点法求系统函数Ha(s)Ha(s) 例:例:已知已知f fp p=5kHz=5kHz,p p=2dB=2dB,f fs s=12kHz=12kHz, s s=30dB=30dB,设计巴特沃斯低通滤波器。,设计巴特沃斯低通滤波器。 解:(解:(1 1)确定阶次)确定阶次N N: 25. 44 . 2lg0242. 0lglg110110lg10/10/psspN 取取N=5N=5,其极点为,其极点为(归一化极点)
26、3455016523754,jjjjjsesesesese(2 2)查表求极点:)查表求极点:P1,2=-0.3090P1,2=-0.3090 j0.9511; j0.9511; p3,4=-0.8090 p3,4=-0.8090 j0.5857; p0=-1.000 j0.5857; p0=-1.000所以所以 )()(10kNkNcasssH(3)求)求 c:所以所以s比题目中给出的指标小比题目中给出的指标小,过渡带符合要求。过渡带符合要求。sKrad/5.275521)(102N10.1pcpsKradNcss/525.102) 110(211 . 0(4 4)去归一化,求)去归一化,求
27、H Ha(S)a(S)将将p=s/p=s/c c代入代入H Ha(P)a(P),得:,得:50412323234455)(ccccccabsbsbsbsbssH切比雪夫滤波器引入原因:切比雪夫滤波器引入原因:Butterworth滤波器频率特性,无论在通带与阻带都随频率单调变化,因此如果在通带边缘满足指标,则在阻带内肯定会有富裕量,也就是会超过指标的要求,因此并不经济。更有效的方法是将指标的精度要求均匀的分布在通带内,或均匀分布在阻带内,或同时均匀分布在通带与阻带内,这时就可设计出阶数较低的滤波器。这种精度均匀分布的办法可通过选择具有等波纹特性的逼近函数来完成。4.2.24.2.2切比雪夫滤波
28、器设计切比雪夫滤波器设计通带内等波纹,阻带内单调通带内等波纹,阻带内单调-切比雪夫切比雪夫1 1型型通带内单调,阻带内等波纹通带内单调,阻带内等波纹-切比雪夫切比雪夫2 2型型切比雪夫切比雪夫1 1型的幅度平方函数:型的幅度平方函数:)(11| )(|222pNaCjH是小于是小于1 1的正数,称为纹波参数,是表示通的正数,称为纹波参数,是表示通带内纹波大小的一个参数,带内纹波大小的一个参数, 愈大,纹波也愈大,纹波也愈大。愈大。p p称为有效通带截止频率。称为有效通带截止频率。频率通常对频率通常对p p归一化,归一化, p 在通带内,在1和 之间起伏变化;在阻带内是单调下降的; 当N为奇数时
29、,滤波器在 处的幅度响应为1;当N为偶数时,滤波器 在 处的幅度响应为 。当 时, 2110 0 211p 21()1aHj 4.2.24.2.2切比雪夫滤波器设计切比雪夫滤波器设计基本性质基本性质的确定的确定 设允许的通带纹波为,那么 22max2min()10lg10lg(1)()aaHjHj210101阶数阶数N N 的确定的确定2221()1()assNpHjC1211()()1()ssNppasCch NchHj12111()()asspchHjNch(1)(1)查表得查表得 (2)查表得查表得幅度平方函数的极点幅度平方函数的极点 其中iiisj 21sin221cos2ipipis
30、hNichN 111( )shN 的确定的确定)(sHa)(sHa极点分布极点分布 2N个等角度间隔(间隔为/N)分布在 为长半轴, 为短半轴的椭圆 上的点。 schssh2222221iiccshch切比雪夫滤波器的传输函数切比雪夫滤波器的传输函数 系数A由s=0时滤波器幅度响应的值确定:当当N N为奇数时,为奇数时,当当N N为偶数时,为偶数时, (0)1aH21(0)1aHNiisssAsH1)()(去归一化得到滤波器的传输函数去归一化得到滤波器的传输函数Ha(s)切比雪夫低通滤波器的设计步骤切比雪夫低通滤波器的设计步骤 (1)(1)由给定的设计指标确定切比雪夫滤波由给定的设计指标确定切
31、比雪夫滤波器的参数器的参数、N N和和p p21010112111()()asspchHjNch(2)确定Ha(s) 1)查表求得归一化传输函数查表求得归一化传输函数 ,令 代替归一化原型滤波器系统函数中的 ,即得到实际滤波器传输函数。cs)(sHas切比雪夫低通滤波器的设计步骤切比雪夫低通滤波器的设计步骤 归一化归一化ChebyshevChebyshev低通滤波器的传输函数为低通滤波器的传输函数为sQksHaa/0aQKkapspspssQ21nnnassasasaaksH112210.)(切比雪夫低通滤波器的设计步骤切比雪夫低通滤波器的设计步骤 归一化归一化ChebyshevChebyshev低通滤波器的传输函数为低通滤波器的传输函数为为了得到单位峰值增益,一般选为了得到单位峰值增益,一般选为偶数为奇数nQnQKaa2100切比雪夫低通滤波器的设计步骤切比雪夫低通滤波器的设计步骤 (2)(2)确定确定Ha(s)Ha(s) 2 2)滤波器的极点,并由)滤波器的极点,并由s s平面左半平面平面左半平面的极点构成的极点构成Ha(s)Ha(s)
温馨提示
- 1. 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
- 2. 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
- 3. 本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
- 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
- 5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
- 6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
- 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
最新文档
- haccp培训合同样本
- 农村销售农资合同样本
- 业主支付模式合同样本
- 上海美容美发劳动合同范例
- 出售工厂车间合同标准文本
- 矿山开采机械进场及使用计划
- 医疗器械开发流程中的知识产权保护
- 如何提升政治课互动性的心得体会
- 科学课堂互动游戏活动计划
- 网络安全保障措施与应对策略
- 西藏林芝嘉园小区项目可研(可研发)
- 丧假证明模板
- summary-writing-概要写作-优质课件
- 按期取得毕业证和学位证承诺书
- T∕CIC 049-2021 水泥窑用固体替代燃料
- 部编版高中语文必修下册第八单元《单元导读》教学设计
- 第五章 学校教育的主要活动形式:课堂教学
- 大会—冠脉微循环障碍
- 《办公自动化》教学教案
- 动物检疫学讲义课件
- 高杆照明灯检修维护规程

评论
0/150
提交评论