中考数学圆专题练习

1、中考数学圆专题练习-一、选择题1.（2010年 湖里区 二次适应性考试）已知半径分别为5 cm和8 cm的两圆相交，则它们的圆心距可能是（ ） A1 cm B3 cm C10 cm D15 cm答案：CAOBCDE2.（2010年教育联合体）如图，已知AB是O的直径，O交BC的中点于D，DEAC于E，连接AD，则下列结论正确的个数是（ ）ADBC，EDAB，OAAC，DE是O的切线A1个 B2个 C3个 D4个第3题答案：D3.（2010安徽省模拟）如图，AB是O的直径，点D、E是圆的三等分点，AE、BD的延长线交于点C，若CE=2,则O中阴影部分的面积是（ ）ABCD 第4题图答案：A4.（

2、2010年重庆市綦江中学模拟1）.在直角坐标系中，A、B的位置如图所示.下列四个点中，在A外部且在B内部的是（ ）A.（1，2） B.(2,1). C.(2,-1). D.(3,1)第5题图 答案C5.(2010年聊城冠县实验中学二模)如下图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为（ ）A2cm BcmCcm Dcm答案C6.（2010年广州市中考六模）、如果圆锥的母线长为6cm，底面圆半径为3cm，则这个圆锥的侧面积为（ ）A. B. C. D. 答案：B7题图7.（2010年广州市中考六模）如图，已知O的弦AB、CD相交于点E，的度数为60°，的度数

3、为100°，则AEC等于（ ）A. 60° B. 100° C. 80° D. 130°答案：C8题图8.（2010年广西桂林适应训练）如图，圆弧形桥拱的跨度AB12米，拱高CD4米，则拱桥的半径为（）A.6.5米B.9米C.13米D.15米9题图答案：A9.（2010年广西桂林适应训练）如图，BD是O的直径，CBD=，则A的度数为（ ）来A.30 B.45 C.60 D.75答案：C10.（2010山东新泰）已知O1的半径为5cm，O2的半径为3cm，圆心距O1O22，那么O1与O2的位置关系是（ ）A相离 B外切 C相交 D内切答案：D11

4、.（2010年济宁师专附中一模）如图，为的四等分点，动点从圆心出发，沿路线作匀速运动，设运动时间为（s），则下列图象中表示与之间函数关系最恰当的是（ ）第11题图ABCDOPBty04590Dty04590Aty04590Cty04590答案：C12.（2010年武汉市中考拟）已知：如图，以定线段AB为直径作半圆O，P为半圆上任意一点（异于A、B），过点P作半圆O的切线分别交过A、B两点的切线于D、C，AC、BD相交于N点，连结ON、NP.下列结论： 四边形ANPD是梯形； ON=NP； DP·PC为定植； PA为NPD的平分线.其中一定成立的是A. B. C. D.答案：B第13题

5、13.（2010 年河南模拟）如图，圆心为A、B、C的三个圆彼此相切，且均与直线l相切，若A、B、C的半径分别为a,b,c,(0cab),则a、b、c一定满足的关系式为（ ）A.2b=a+cB. C. D.答案：D14.（2010年湖南模拟）O1和O2半径分别为4和5,O1O2=7,则O1和O2的位置关系是( ) A.外离 B.相交 C.外切 D.内含答案：B15.（2010年湖南模拟）圆锥的母线长为3,底圆半径为1,则圆锥的侧面积为( ) A.3 B.4 C. D.2第16题答案：A16.(2010年厦门湖里模拟)如图，正三角形ABC内接于，动点在圆周的劣弧AB上，且不与A、B重合，则BPC

6、等于 A B C D答案：B17.（2010年西湖区月考）如图，一种圆管的横截面是同心圆的圆环面，大圆的弦AB切小圆于点C，大圆弦AD交小圆于点E和F为了计算截面(图中阴影部分)的面积，甲、乙、丙三位同学分别用刻度尺测量出有关线段的长度甲测得AB的长，乙测得AC的长，丙测得AD的长和EF的长其中可以算出截面面积的同学是( )A甲、乙 B丙C甲、乙、丙 D无人能算出答案：C18.（2010年西湖区月考）四个半径为的圆如图放置，相邻两个圆交点之间的距离也为，不相邻两个圆的圆周上两点间的最短距离等于2，则的值是( )A B C D答案：A19.（2010年铁岭加速度辅导学校）如图（3），已知AB是半

7、圆O的直径，BAC=32º，D是弧AC的中点，那么DAC的度数是（ ）A.25º B.29º C.30º D.32°答案：B20.（2010年天水模拟）已知两圆的半径分别为3和4，圆心距为8，那么这两个圆的位置关系是（ ）A.内切 B.相交 C.外离 D.外切答案：C二、填空题1.（2010年河南模拟）圆内接四边形ABCD的内角A:B:C=2：3：4，则D_°第2题答案：902.（2010年 河南模拟）如图，已知O的半径为R，AB是O的直径，D是AB延长线上一点，DC是O的切C是切点，连接AC,若CAB=300，则BD的长为 答案：R

8、；第3题3.（2010年 河南模拟）如图，是一张电脑光盘的表面，两个圆心都是O,大圆的弦AB所在的直线是小圆的切线，切点为C，已知大圆的半径为5cm，小圆的半径为1cm，则弦AB的长是多少？ 答案：4题4.（2010年广东省中考拟）如图2，AB是O的直径，COB=70°，则A=_度答案.35.5.（2010年武汉市中考拟）如图，点在轴上，交轴于两点，连结并延长交于，过点的直线交轴于，且的半径为，若函数（x<0）的图象过C点，则k=_答案：-46.（2010年铁岭加速度辅导学校）如图，在矩形空地上铺4块扇形草地若扇形的半径均为米，圆心角均为，则铺上的草地共有 平方米（第6题）答案

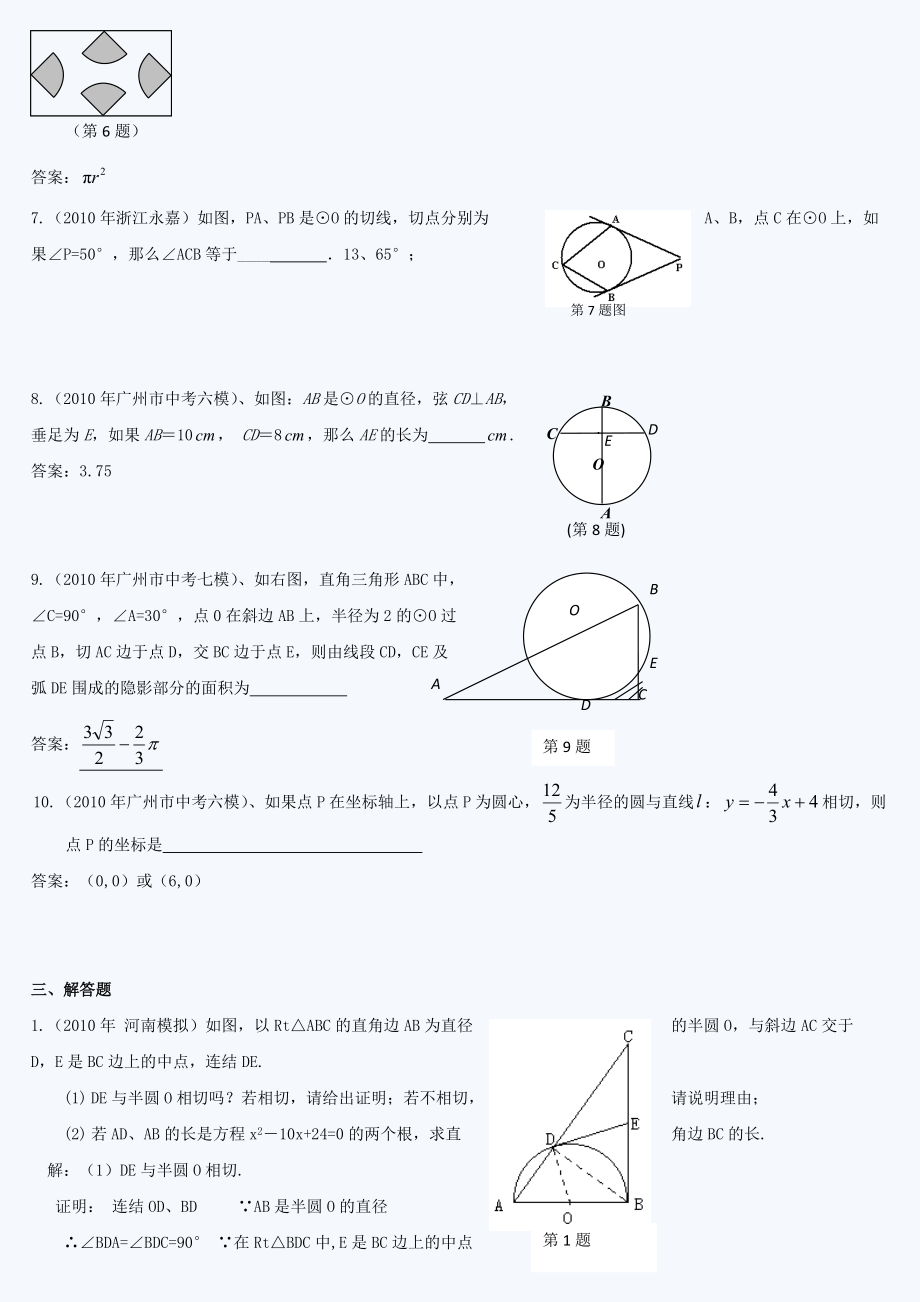
9、：第7题图7.（2010年浙江永嘉）如图，PA、PB是O的切线，切点分别为A、B，点C在O上，如果P=50°，那么ACB等于_ 13、65°；CABEDO.(第8题)8.（2010年广州市中考六模）、如图：AB是O的直径，弦CDAB，垂足为E，如果AB10， CD8，那么AE的长为 .答案：3.75DEACBO第9题9.（2010年广州市中考七模）、如右图，直角三角形ABC中，C=90°，A=30°，点0在斜边AB上，半径为2的O过点B，切AC边于点D，交BC边于点E，则由线段CD，CE及弧DE围成的隐影部分的面积为 答案：10.（2010年广州市中考六

10、模）、如果点P在坐标轴上，以点P为圆心，为半径的圆与直线：相切，则点P的坐标是 答案：（0,0）或（6,0）三、解答题第1题1.（2010年 河南模拟）如图，以RtABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连结DE. (1) DE与半圆O相切吗？若相切，请给出证明；若不相切，请说明理由；(2) 若AD、AB的长是方程x210x+24=0的两个根，求直角边BC的长.解：（1）DE与半圆O相切. 证明： 连结OD、BD AB是半圆O的直径 BDA=BDC=90° 在RtBDC中,E是BC边上的中点DE=BEEBDBDEOB=ODOBD=ODB 又ABCOBD

11、+EBD90°ODB+EBD=90°DE与半圆O相切. （2）解：在RtABC中，BDAC RtABDRtABC = 即AB2=AD·AC AC= AD、AB的长是方程x210x+24=0的两个根 解方程x210x+24=0得： x1=4 x2=6 AD<AB AD=4 AB=6 AC=9 在RtABC中，AB=6 AC=9 BC=3 第2题2.（2010年湖南模拟）如图4,平行四边形ABCD中,以A为圆心,AB为半径的圆分别交AD、BC于F、G,延长BA交圆于E.求证:EF=FG. 证明:连结AG.A为圆心,AB=AG.ABG=AGB.四边形ABCD为平行

12、四边形.ADBC.AGB=DAG,EAD=ABG.DAG=EAD.第3题3.（2010年湖南模拟）如图 ,以ACF的边AC为弦的圆交AF、CF于点B、E,连结BC,且满足AC2=CE·CF.求证:ABC为等腰三角形.证明:连结AE.AC2=CE·CF, 又ACE=FCA.ACEFCA. AEC=FAC. . AC=BC,ABC为等腰三角形.4.（2010年 中考模拟2）如图，有一个圆O和两个正六边形， .的6个顶点都在圆周上，的6条边都和圆O相切（我们称，分别为圆O的内接正六边形和外切正六边形） .（1）设，的边长分别为，圆O的半径为，求及的值；（2）求正六边形，的面积比的

13、值 .答案：（1）连接圆心O和T的6个顶点可得6个全等的正三角形 .所以ra=11;连接圆心O和T相邻的两个顶点，得以圆O半径为高的正三角形，所以rb=2;（2） TT的连长比是2，所以SS=5.（2010年 中考模拟2）如图是一个几何体的三视图 .（1）写出这个几何体的名称；（2）根据所示数据计算这个几何体的表面积；（3）如果一只蚂蚁要从这个几何体中的点B出发，沿表面爬到AC的中点D，请你求出这个线路的最短路程 .答案：（1） 圆锥；（2） 表面积S=（平方厘米）（3） 如图将圆锥侧面展开，线段BD为所求的最短路程 .由条件得，BAB=120°，C为弧BB中点，所以BD= .6.（

14、2010年长沙市中考模拟）AEDOBCF在中，是边上一点，以为直径的与边相切于点，连结并延长，与的延长线交于点（1）求证：；（2）若，求的面积答案：1）证明：连结。切于，又即，。又， 。（2）设半径为，由得，即，解之得（舍）。第7题图7.（2010年 湖里区 二次适应性考试）已知：如图，ABC的中，AB=AC，点B、C都在O上，AB、AC交O于D、E两点，求证：答案：证明：AB=AC BC 8.（2010年 湖里区 二次适应性考试）如图，线段AB与O相切于点C，连结OA，OB，第8题图COABDOB交O于点D，已知，（1）求O的半径；（2）求图中阴影部分的面积答案：（1）连结OC，AB与O相切

15、于点C ， 在中， O的半径为3 （2）在中 OC=, B=30o, COD=60o 扇形OCD的面积为= 阴影部分的面积为= 9.（2010年 湖里区 二次适应性考试）如图，四边形ABCD内接于O，BD是O的直径，AECD于点E，DA平分BDE。（1）求证：AE是O的切线。第9题图（2）若DBC=30°，DE=1 cm，求BD的长。答案：（1）证明：连结OAAD平分BDEADEADOOA=ODOADADOADEOAD OACEAECDAEOA AE是O的切线 （2）BD是O的直径BCD90° DBC=30°BDE120°AD平分BDEADEADO=60

16、°OA=ODOAD是等边三角形 AD=OD=BD 在RtAED中，DE=1，ADE=60°AD= = 2 yxCBAMO4213（第10题图）BD=4 10.（2010年 湖里区 二次适应性考试）已知：如图，直径为的与轴交于点O、A，点把弧OA分为三等分，连结并延长交轴于D（0，3）.（1）求证：； （2）若直线：把的面积分为二等分，求证：答案：证明： （1）连接，OA是直径，且把弧OA三等分， 又， 又OA为直径， ， 在和中， （ASA） yxCBAMO42135（2）若直线把的面积分为二等份， 则直线必过圆心， ，在Rt中， ， 把 代入得：ABO11.（2010年北

17、京市朝阳区模拟）如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点的三个顶点、都在格点上（1）画出绕点逆时针旋转后得到的三角形；（2）求在上述旋转过程中所扫过的面积DEABO解：（1）画图正确（如图）（2）所扫过的面积是：12.(2010年聊城冠县实验中学二模) 如下图所示，以RtABC的直角边AB为直径作圆O，与斜边交于点D，E为BC边上的中点，连接DE。（1）求证：DE是O的切线；（2）连接OE，AE，当CAB为何值时，四边形AOED是平行四边形？解（1）连接OD与BDBDC是Rt，且E为BC中点EDBEBD又ODOB且EBD+DBO90°EDBODB90&

18、#176;DE是O的切线（2）EDOB90°，若要AOED是平行四边形，则DEAB，D为AC中点又BDACABC为等腰直角三角形CAB45°13.（2010年广西桂林适应训练）、以RtABC的直角边AB为直径作圆O，与斜边交于点D,E为BC边上的中点，连接DE.第13题（1）求证：DE是O的切线；（2）连接OE、AE，当CAB为何值时，四边形AOED是平行四边形？并在此条件下求sinCAE的值.答案：（1）连接OD、BD BDC是Rt, 且E为BC中点。EDB=EBD. 又OD=OB 且EBD+DBO=90° EDB+ODB=90°DE是O的切线； （2

19、）EDO=B=90°,若要AOED是平行四边形，则DEAB,D为AC中点。又BDAC,ABC为等腰直角三角形。CAB=45°. 过E作EHAC于H.设BC=2k，则EH= sinCAE= 14.（2010年山东新泰）在某张航海图上，标明了三个观测点的坐标为O（0，0）、B（12，0）、C（12，16），由三个观测点确定的圆形区域是海洋生物保护区，如图所示（1）求圆形区域的面积（取3.14）；（2）某时刻海面上出现一渔船A，在观测点O测得A位于北偏东45°方向上，同时在观测点B测得A位于北偏东30°方向上，求观测点B到渔船A的距离（结果保留三个有效数字）；

20、（3）当渔船A由（2）中的位置向正西方向航行时，是否会进入海洋生物保护区？请通过计算解释（1）314；（2）16.4；（3）28.4>18，所以渔船A不会进入海洋生物保护区 A BO F E D C15.（2010年浙江杭州）已知：如图，AB是O的直径，点C、D为圆上两点，且弧CB弧CD，CFAB于点F，CEAD的延长线于点E （1）试说明：DEBF； （2）若DAB60°，AB6，求ACD的面积 （1） 弧CB=弧CD CB=CD，CAE=CAB又 CFAB，CEAD CE=CF CEDCFB DE=BF（2）易得：CAECAF易求： xyOPA-216.（2010年江西南昌

21、一模）如图，在平面直角坐标系中，直线OA与轴的夹角为，以P为圆心， 为半径作P,与交于点.(1) 当r为何值时，为等边三角形？(2) 当P与直线相切时,求的值.答案：（1）作于M.是等边三角形,xyOPA-2CM(2)连结与直线相切,P的半径为4+2=6.则17.(2010年厦门湖里模拟) 如图，已知在O中，AB=4，AC是O的直径，ACBD于F，A=30°.（1）求图中阴影部分的面积；ABDOFC（2）若用阴影扇形OBD围成一个圆锥侧面，请求出这个圆锥的底面圆的半径.答案：（1）A=30° ACBD BF= BOC=COD=60° OB=2OFOF=2，OB=4

22、S阴= （2）根据题意得: = 18.(2010年厦门湖里模拟)如图，已知AB是O的直径，点C在O上，P是OAC的重心，且OP，A30ºAOBDCP(1)求劣弧的长；(2)若ABD120º，BD1，求证：CD是O的切线答案：.(1)解：延长OP交AC于E， P是OAC的重心，OP， OE1， 且 E是AC的中点. OAOC， OEAC. 在RtOAE中， A30°，OE1， OA2. AOE60°. AOC120°. . (2)证明：连结BC. E、O分别是线段AC、AB的中点， BCOE，且BC2OE2OBOC. OBC是等边三角形. 法1： OBC60°. OBD120°， CBD60°AOE. BD1OE，BCOA， OAE BCD. BCD30°. OCB60°， OCD90°. CD是O的切线. 法2：过B作BFDC交CO于F. BOC60°，ABD120°, OCBD. 四边形BDCF是平行四边形. CFBD1. OC2， F是OC的中