投入产出模型

1、.14.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 投入产出分析由美国经济学家W.Leontief于20世纪30年代首先提出，其基本思想是：利用线性代数的理论和方法，研究一个经济系统的各部门之间错综复杂的联系，建立相应的数学模型，用于经济分析和预测. 设一个经济系统有个部门：部门1，部门2，部门n，且规定：（1）部门i仅生产一种产品i（部门i的产出）.不同部门的产品不能相互替代，即部门与产出一一对应；（2）在生产过程中，部门j至少需要消耗另一部门i的产品（部门i对部门j的投入），且部门i对部门j的投入与部门i的产出成正比. .24.6.1 4.6.1 应应 用（二）用（

2、二）投入产出分析投入产出分析 投入产出模型按计量单位的不同，可分为价值型投入产出模型和实物型投入产出模型.在价值型投入产出模型中，各部门的投入，产出均以货币为单位来计量；在实物型投入产出模型中，各部门的投入，产出均以实物为单位来计量. .34.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 先来研究价值型投入产出模型.根据往年资料可知， 部门i的中间产出，ixijxnjijx1部门i的最终产出， njijiixxy1., 2 , 1ni部门i的产出，部门i对各部门j的投入,.44.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 部门j的纯收入，jmjVj

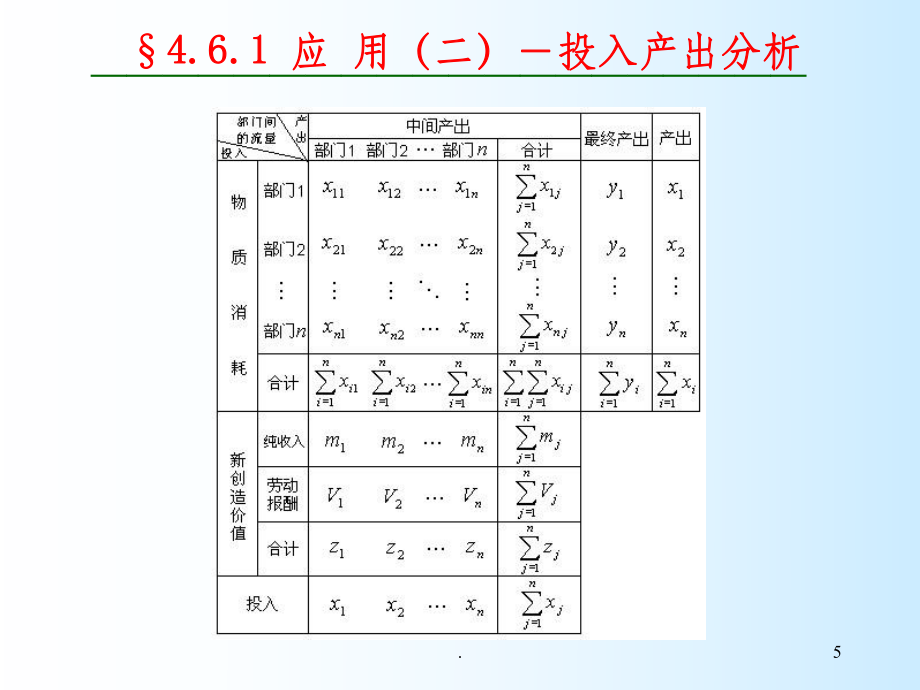
3、jjVmZnj, 2 , 1根据上述资料，编制价值型投入产出表： 部门j的新创造价值部门j的劳动报酬，.54.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 .64.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 由投入产出表易有 （投入新创造价值物质消耗）nixyxnjijii, 2 , 1,1njxzxniijjj, 2 , 1,1产品分配平衡方程组：（6.1）产值构成平衡方程组：（6.2）.74.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 引入直接消耗系数 njixxajijij, 2 , 1,显然，aij表示生产单位产品j

4、所需直接消耗产品i 的数量.由直接消耗系数的定义知， njixaxjijij, 2 , 1,（1）代入（6.1）得 nixayxnjjijii, 2 , 1,1.84.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 nnnnnnnnnnnyxaxaxaxyxaxaxaxyxaxaxax2211222221212112121111（6.3）令 nxxxX21（产出向量）， nyyyY21（投入向量）， .94.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 nnnnnnaaaaaaaaaA212222111211（直接消耗系数矩阵）， 则（6.3）即为 Y

5、AXX或 YXAE)(直接消耗系数矩阵的性质： 性质1 ., 2 , 1, 0njiaij （6.4） .104.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 证 njixxajijij, 2 , 1, 0. 性质2 ., 2 , 1, 11njaniij 证,1111 ,11111kniikniikknikikniikniikxxxxxxaankk，则，有（反证法）假设推论njiaij, 2 , 1, 10矛盾.114.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 . 1|, 2 , 1, 1|, 2 , 1, 1|)(17. 411，有的特征值则

6、或，若设矩阵AnjaniaaAThniijnjijnnij 证的特征向量为属于特征值设矩阵A021nxxx., 2 , 1, 1|1的情况仅需证若nianjij.124.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 则 ,Anixxainjjij, 2 , 1,1即令 , 0|max|1inikxxnjkjkjnjkjkjnjkjkjknjjkjkkkkxxaxxaxxaxxaxxxx1111|1|则njkjnjkjnjkjkjaaxxa1111|.134.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 若, 2 , 1, 1|1nianjij1|1n

7、jkja则. 1|满足的任一特征值则为直接消耗系数矩阵，设AA证 由推论1及Th4.15知， . 0)(01kkAAEAEA且可逆，则为直接消耗系数矩阵，设).(0kAk.证 性质1，2 + Th4.17.推论1推论2.144.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 再由Th4.16知，即证. .0)(001预测和分析展作出，从而对未来的经济发则，根据上述讨论，若根据上述讨论，若YAEXYY（2）代入（6.2）得 njxazxnijijjj, 2 , 1,1即 nnnnnnnnnnnzxaxaxaxzxaxaxaxzxaxaxax212222222122111121

8、1111（6.5） .154.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 令 nzzzZ21（新创造价值向量）， niinniiniiaaaD11211.164.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 则（6.5）即为 ZDXX或 ZXDE)(矩阵D的性质： . 0)(1DEDE可逆，且证 利用直接消耗系数矩阵的性质2验证即可. 0)(01ZDEXZ，则根据以上讨论，若例例 下表为根据某地区某年的统计资料编制的投入产出表， （6.6）（6.4）和（6.6）合称为价值型投入产出模型. .174.6.1 4.6.1 应应 用（二）用（二）投入产出

9、分析投入产出分析 又计划下一年农业，工业，服务业的最终需求分别为135，13820，1023，试对该地区下一年的经济发展作出预测和分析. 解：易求直接消耗系数矩阵为 1077. 00114. 01192. 01282. 04410. 03005. 00014. 00018. 01399. 0A.184.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 于是 1243. 10234. 01640. 02591. 07962. 16635. 00024. 00038. 01643. 1)(1AE（可利用Mathematica软件计算） 又 ,102313820135Y4 .149

10、60 .251781 .212)(1YAEX.194.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 故预计下一年农业，工业，服务业的总产出分别为 4 .1496, 0 .25178, 1 .212321xxx从而，可得下一年农业，工业，服务业三个部门间的流量，以及下一年农业，工业，服务业三个部门的新创造价值. 根据上述得到的数据，编制下一年的投入产出表如下 ：.204.6.1 4.6.1 应应 用（二）用（二）投入产出分析投入产出分析 据此可为决策提供科学依据. .214.6.2 4.6.2 应应 用（二）用（二）投入产出分析投入产出分析 直接消耗系数aij,i,j=1,

11、2,n表示部门j生产单位产品j所需直接消耗的部门i的产品i的数量.然而，一般而言，部门j除直接消耗部门i的产品外，还要通过一系列中间环节间接消耗部门i的产品.直接消耗与间接消耗的和称为完全消耗. 令aij= 部门j生产单位产品j所需完全消耗的部门i的产品 的数量，nnnnnnbbbbbbbbbB212222111211（完全消耗系数矩阵）， .224.6.2 4.6.2 应应 用（二）用（二）投入产出分析投入产出分析 则由完全消耗的定义知nkkjikijijabab1BAABAAEB)(.)()()(111EAEAEAEEAEAB又由定理4.13知，,)(21kAAAEAE.)(22kkAAA

12、EAAAEBBEAEEAEB11)()(再由前面的结论， YBEYAEX)()(1即或解之得于是，令.234.6.2 4.6.2 应应 用（二）用（二）投入产出分析投入产出分析 部门i的最终产出，ijqnji, 2 , 1,iQiq 部门j新创造的价值，jpjz 编制价值型投入产出表： 部门i对部门j的投入，部门i的产出，产品j的价格，.244.6.2 4.6.2 应应 用（二）用（二）投入产出分析投入产出分析 由投入产出表有 niqqQnjijii, 2 , 1,1（6.1） njqpzQpnjijijjj, 2 , 1,1（6.2） .254.6.2 4.6.2 应应 用（二）用（二）投入

13、产出分析投入产出分析 引入直接消耗系数 njiQqajijij, 2 , 1,. 0ijijaija，且的数量所需直接消耗产品表示生产单位产品显然， 由直接消耗系数的定义知， . njiQaqjijij, 2 , 1,（1）代入（6.1）得 niQaqQnjjijii, 2 , 1,1即 .264.6.2 4.6.2 应应 用（二）用（二）投入产出分析投入产出分析 nnnnnnnnnnnqQaQaQaQqQaQaQaQqQaQaQaQ2211222221212112121111 （6.3） 令 nQQQQ21nqqqq21.274.6.2 4.6.2 应应 用（二）用（二）投入产出分析投入产出

14、分析 nnnnnnaaaaaaaaaA212222111211（直接消耗系数矩阵）， 则（6.3）即为 qQAQ或 qQAE)( （6.4） （2）由（6.2）得 .284.6.2 4.6.2 应应 用（二）用（二）投入产出分析投入产出分析 njQqpQzpnjjijijjj, 2 , 1,1令 njQzzjjj, 2 , 1, 则上式即为 njapzpnjijijj, 2 , 1,1或 nnnnnnnnnnnzpapapapzpapapapzpapapap2211222221122112211111（6.5） .294.6.2 4.6.2 应应 用（二）用（二）投入产出分析投入产出分析 令

15、npppp21nzzzZ21则（6.5）即为 ZpApT或 TTZAEp)( （6.6） （6.4）和（6.6）合称为实物型投入产出模型. .304.6.2 4.6.2 应应 用（二）用（二）投入产出分析投入产出分析 两个消耗系数矩阵之间的一个关系： 定理4.18 . AA 证 由价值型和实物型投入产出模型的两张投入产出表知， , 2 , 1,njiqpxijiij., 2 , 1,njqpxjjj 于是， ., 2 , 1,njiappaappqpqpxxaijijijijjijjijijijij.314.6.2 4.6.2 应应 用（二）用（二）投入产出分析投入产出分析 故 nnnnnnnnnnnnnnnnnnappappappappappappappappappaaaaaaaaaA221122222221211112121111212222111211.324.6.2 4.6.2 应应 用（二）用（二）投入产出分析投入产出分析 nnnnnnnnpppaaaaaaaaappp0000001112121222211121121.33