【课件】6.3.1平面向量基本定理课件高一数学人教A版（2019）必修第二册

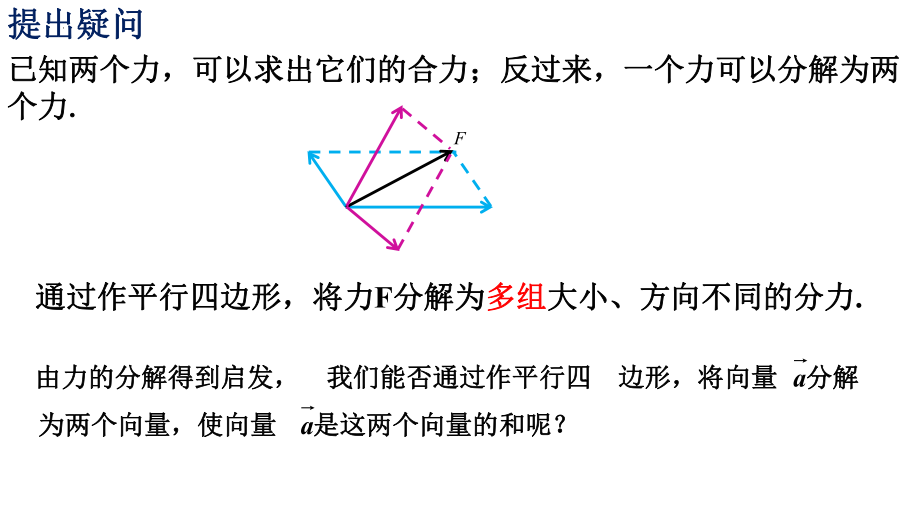
1、6.3.1平面向量基本定理平面向量基本定理 向量向量 与非零向量与非零向量 共线当且仅当共线当且仅当有且只有有且只有一个实数一个实数，使得，使得 向量共线定理向量共线定理abab 1、当当 0时：时：2、当、当 0时：时：3、当、当 =0时：时：方向：方向：长度：长度：|ab 方向相同方向相同与与ab方向相反方向相反与与ab00 ab已知两个力，可以求出它们的合力；反过来，一个力可以分解为两已知两个力，可以求出它们的合力；反过来，一个力可以分解为两个力个力. .F通过作平行四边形，将力通过作平行四边形，将力F分解为分解为多组多组大小、方向不同的分力大小、方向不同的分力.是是这这两两个个向向量量

2、的的和和呢呢？为为两两个个向向量量，使使向向量量分分解解边边形形，将将向向量量我我们们能能否否通通过过作作平平行行四四由由力力的的分分解解得得到到启启发发，aa提出疑问提出疑问1e2e OCABMNa思考：一个平面内的两个不共线的向量思考：一个平面内的两个不共线的向量 与该平面内的与该平面内的任一向任一向量量 之间的关系之间的关系21ee 、aONOMOC 如图如图111eOAOM 222eOBON 2211eeOC 2211eea 即即1e2e OCABMNaONOMOC 如图如图111eOAOM 222eOBON 2211eeOC 2211eea 即即来来表表示示呢呢？是是否否也也能能由由

3、唯唯一一一一对对共共线线的的非非零零向向量量时时，或或是是与与当当2121, aeea2211eea 即即.01221，即即可可使使结结论论成成立立为为或或共共线线时时，可可令令或或与与当当 eea1e2e1e2eaa的的形形式式也也可可以以表表示示成成是是零零向向量量时时，当当2211eeaa 形形式式是是唯唯一一的的的的形形式式，而而且且这这种种表表示示的的方方向向分分解解，表表示示成成，都都可可以以按按平平面面内内任任一一向向量量221121eeeea 2211eea 1e2e1e2eaa一、平面向量基本定理：一、平面向量基本定理： 如果如果 是同一平面内的两个是同一平面内的两个不共线不

4、共线向量，那么对于向量，那么对于这一平面内的任一向量这一平面内的任一向量 有且只有有且只有一对实数一对实数1、2, ,使使21ee 、a其中其中 叫做表示这一平面内所有向量的一组叫做表示这一平面内所有向量的一组基底基底21,ee2211eea 特别的，若特别的，若 ，则有且只有，则有且只有 ：0 a021 22110ee 可使可使特别的，若特别的，若 与与 共线，则有共线，则有2=0( 1=0)，使得，使得:a)(21ee2211eea 2、基底不唯一，关键是、基底不唯一，关键是不共线不共线.4、基底给定时，分解形式、基底给定时，分解形式唯一唯一.说明：说明：1、基底基底 不共线且是非零向量；

5、不共线且是非零向量；3、由定理可将任一向量、由定理可将任一向量 在给出基底在给出基底 的条件下进行分解的条件下进行分解.21ee ，a21ee ，,.5,.33,.,.)(,12112121212121eeeDeeCeeeeBeeAee 做做基基底底的的是是量量中中不不能能共共线线向向量量，以以下下各各组组向向是是同同一一平平面面内内的的两两个个不不、设设B随堂练习随堂练习作为基底条件：不共线！作为基底条件：不共线！B2、设、设O是是ABCD两对角线的交点，下列向量组：两对角线的交点，下列向量组：其中可作为这个平行四边形所在平面表示它的所有向量的基底其中可作为这个平行四边形所在平面表示它的所有

6、向量的基底( )A、(1)(2) B、(1)(3)C、(1)(4) D、(3)(4).)4()3(2)1(OBODDCCABCDAADAB与与；与与；与与）（；与与DABCO作为基底条件：不共线！作为基底条件：不共线！3、如果如果 平面平面内所有向量的一个基底，那么下列说法正确的是内所有向量的一个基底，那么下列说法正确的是A.若存在实数若存在实数1，2使使 ，则，则120B.对空间任意向量对空间任意向量 都可以表示为都可以表示为 ，其中，其中1，2RC. (1，2R)不一定在平面不一定在平面内内D.对于平面对于平面内任意向量内任意向量 ，使，使 的实数的实数1，2有无数对有无数对A解析：解析：

7、B错，这样的错，这样的 只能与只能与 在同一平面内，不能是空间任意向量在同一平面内，不能是空间任意向量；C错，在平面错，在平面内任意向量都可表示为内任意向量都可表示为 的形式，故的形式，故 一一定在平面定在平面内内；D错，这样的错，这样的1，2是唯一的，而不是无数对是唯一的，而不是无数对.21ee ，02211 ee a2211eea 2211ee a2211eea a21ee ，2211ee 2211ee 4、给出下列三种说法：给出下列三种说法：一个平面内只有一组不共线的向量可作为表示该平面内所有向一个平面内只有一组不共线的向量可作为表示该平面内所有向量的基底量的基底；一个平面内有无数组不共

8、线向量可作为表示该平面内所有向量一个平面内有无数组不共线向量可作为表示该平面内所有向量的基底的基底；零向量不可作为基底中的向量零向量不可作为基底中的向量.其中，说法正确的为其中，说法正确的为A. B. C. D.BOPOBOARtABtAPOBOA表示表示用用不共线，且不共线，且、如图，、如图，例例,),(,1 OABPABtAP 解：解：)(OAOBtOAOP OBtOAtOP )1(，你有什么发现？，你有什么发现？观察观察OBtOAtOP )1(tt )1(11,2121 ，则则三三点点共共线线，若若OBOAOPBAP.212是是直直角角三三角角形形，用用向向量量方方法法证证明明的的中中线

9、线，是是、例例ABCABCDABCCD ABDC,bDAaCD 解：设解：设ba CA则则, ba CBb, ba )()(babaCBCA 22ba |,|ba 则则0 CBCA CBCA 即即是直角三角形是直角三角形ABC P27 练习练习1.1CFBEADABbabCBaCAABCCFBEAD，表表示示，用用，的的三三条条中中线线，是是，、如如图图， AFEDCBabCACBAB abaabCAABACABAD 21)(21)(21)(21ababbABCBBABCBE21)(21)(21)(21 )(21)(21abCACBCF 的的关关系系吗吗？，得得出出能能由由；，表表示示，用用的

10、的三三等等分分点点是是的的中中点点，是是分分别别，点点，的的两两条条对对角角线线相相交交于于点点、如如图图，平平行行四四边边形形BFDEOGFBDEbaCDDGCDGOCOAFEbADaABOABCD)1()2()1()31(2 ABECDFOG平行且相等P27 练习练习2baADABAC 解解：ADAEDE ADAC 41bba )(41ba4341 AFABFB ACAB43 )(43baa ba4341 AODGADOG ACABAD2131 )(2131baab ba2161 例例2、已知平行四边形、已知平行四边形ABCD中中,M,N分别是分别是BC,DC的中点且的中点且 用用 表示表示 . , aAB ba,ANAM,ADBCMNbaBMABAM 解：解：DNADAN BCAB21 ABADDCAD2121 ADAB21 ba21 ab21 bAD bDC21解：DCADBABCbab21ba21ANDAMDMNbab21)21(21ab41MNBCDCbabABaADBADCNMCDABCDABABCD,2,/2为基底表示