



版权说明:本文档由用户提供并上传,收益归属内容提供方,若内容存在侵权,请进行举报或认领
文档简介
1、第2讲 空间几何体的表面积与体积A级基础演练(时间:30分钟满分:55分)一、选择题(每小题5分,共20分)1(2013·东北三校一模)一个几何体的三视图如图所示,则侧视图的面积为()A2 B1C22 D4解析依题意得,该几何体的侧视图的面积等于22×2×4.答案D2(2011·湖南)设右图是某几何体的三视图,则该几何体的体积为 ()A.12B.18C942D3618解析该几何体是由一个球与一个长方体组成的组合体,球的直径为3,长方体的底面是边长为3的正方形,高为2,故所求体积为2×32318.答案B3一个几何体的三视图如图所示,那么此几何体的
2、侧面积(单位:cm2)为 ()A48 B64 C80 D120解析据三视图知,该几何体是一个正四棱锥(底面边长为8),直观图如图,PE为侧面PAB的边AB上的高,且PE5.此几何体的侧面积是S4SPAB4××8×580(cm2)答案C4(2012·新课标全国)已知三棱锥SABC的所有顶点都在球O的球面上,ABC是边长为1的正三角形,SC为球O的直径,且SC2,则此棱锥的体积为()A. B. C. D.解析在直角三角形ASC中,AC1,SAC90°,SC2,SA;同理SB.过A点作SC的垂线交SC于D点,连接DB,因SACSBC,故BDSC,故S
3、C平面ABD,且平面ABD为等腰三角形,因ASC30°,故ADSA,则ABD的面积为×1× ,则三棱锥的体积为××2.答案A二、填空题(每小题5分,共10分)5已知S、A、B、C是球O表面上的点,SA平面ABC,ABBC,SAAB1,BC,则球O的表面积等于_解析将三棱锥SABC补形成以SA、AB、BC为棱的长方体,其对角线SC为球O的直径,所以2RSC2,R1,表面积为4R24.答案46(2012·天津)一个几何体的三视图如图所示(单位:m),则该几何体的体积为_ m3.解析由三视图可知,该几何体是组合体,上面是长、宽、高分别是6,
4、3,1的长方体,下面是两个半径均为的球,其体积为6×3×12×××3189(m3)答案189三、解答题(共25分)7(12分)如图,已知某几何体的三视图如下(单位:cm):(1)画出这个几何体的直观图(不要求写画法);(2)求这个几何体的表面积及体积解(1)这个几何体的直观图如图所示(2)这个几何体可看成是正方体AC1及直三棱柱B1C1QA1D1P的组合体由PA1PD1,A1D1AD2,可得PA1PD1.故所求几何体的表面积S5×222×2×2××()2224(cm2),体积V23×(
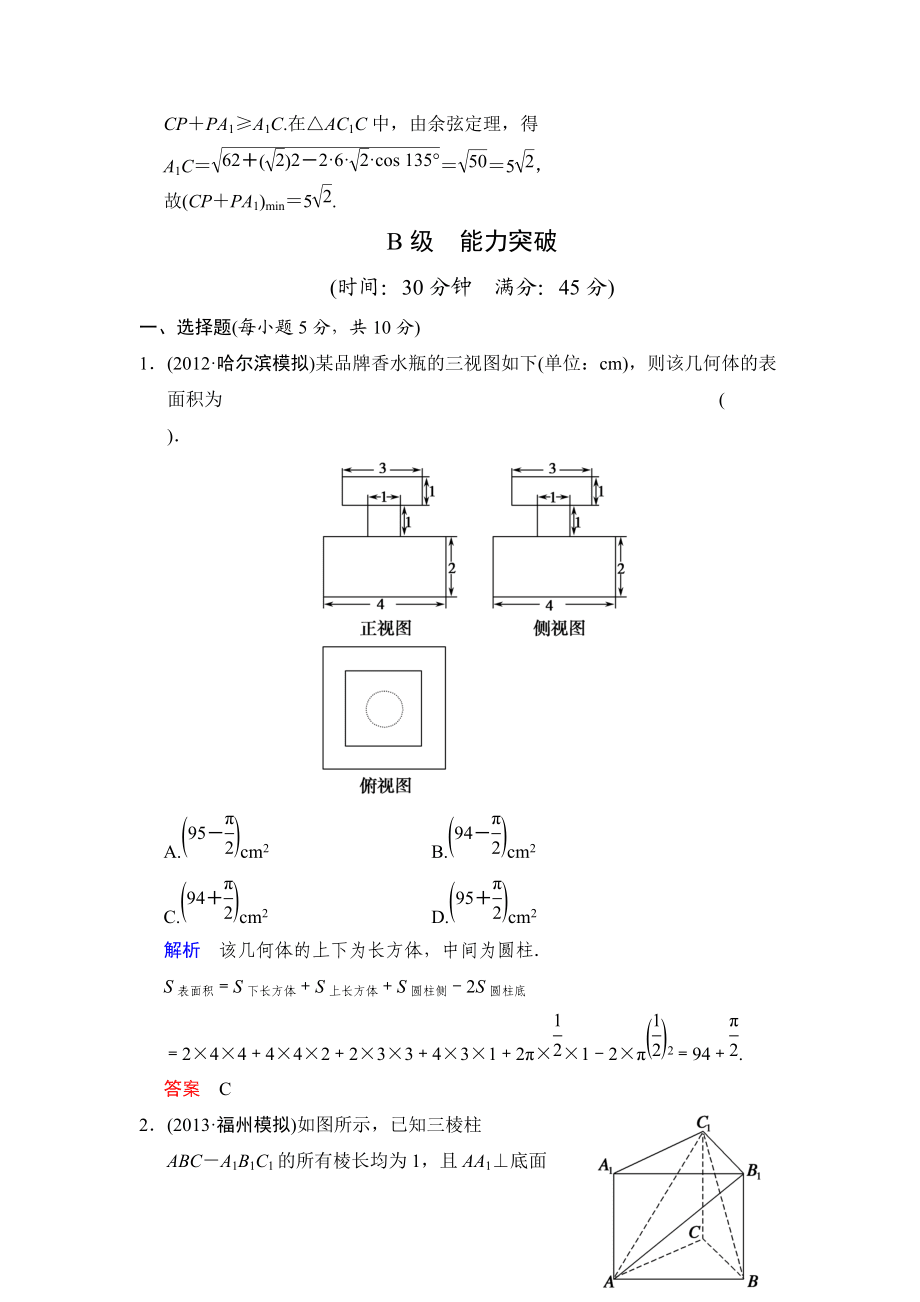
5、)2×210 (cm3)8(13分)在直三棱柱ABCA1B1C1中,底面为直角三角形,ACB90°,AC6,BCCC1,P是BC1上一动点,如图所示,求CPPA1的最小值解PA1在平面A1BC1内,PC在平面BCC1内,将其铺平后转化为平面上的问题解决铺平平面A1BC1、平面BCC1,如图所示计算A1BAB1,BC12,又A1C16,故A1BC1是A1C1B90°的直角三角形CPPA1A1C.在AC1C中,由余弦定理,得A1C5,故(CPPA1)min5.B级能力突破(时间:30分钟满分:45分)一、选择题(每小题5分,共10分)1(2012·哈尔滨模拟
6、)某品牌香水瓶的三视图如下(单位:cm),则该几何体的表面积为 ()A.cm2 B.cm2C.cm2 D.cm2解析该几何体的上下为长方体,中间为圆柱S表面积S下长方体S上长方体S圆柱侧2S圆柱底2×4×44×4×22×3×34×3×12××12×294.答案C2(2013·福州模拟)如图所示,已知三棱柱ABCA1B1C1的所有棱长均为1,且AA1底面ABC,则三棱锥B1ABC1的体积为 ()A. B.C. D.解析三棱锥B1ABC1的体积等于三棱锥AB1BC1的体积,三棱锥
7、AB1BC1的高为,底面积为,故其体积为××.答案A二、填空题(每小题5分,共10分)3(2013·江西盟校二联)已知某几何体的直观图及三视图如图所示,三视图的轮廓均为正方形,则该几何体的表面积为_解析借助常见的正方体模型解决由三视图知,该几何体由正方体沿面AB1D1与面CB1D1截去两个角所得,其表面由两个等边三角形、四个直角三角形和一个正方形组成计算得其表面积为124.答案1244(2012·长春二模)如图所示,正方体ABCDA1B1C1D1的棱长为6,则以正方体ABCDA1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥
8、的全面积为_解析设O为正方体外接球的球心,则O也是正方体的中心,O到平面AB1D1的距离是体对角线长的,即为.又球的半径是正方体对角线长的一半,即为3,由勾股定理可知,截面圆的半径为2,圆锥底面面积为S1·(2)224,圆锥的母线即为球的半径3,圆锥的侧面积为S2×2×318.因此圆锥的全面积为SS2S11824(1824).答案(1824)三、解答题(共25分)5(12分)(2013·杭州模拟)如图,在四边形ABCD中,DAB90°,ADC135°,AB5,CD2,AD2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积解由已知得:CE2,DE2,CB5,S表面S圆台侧S圆台下底S圆锥侧(25)×5×25×2×2(604),VV圆台V圆锥(·22·52)×4×22×2.6(13分)如图(a),在直角梯形ABCD中,ADC90°,CDAB,AB4,ADCD2,将ADC沿AC折起,使平面ADC平面ABC,得到几何体DABC,如图(b)所示(1)求证:BC平面ACD;(2)求几何体DABC的体积(1)证明在图中,可得ACBC2,从而AC2B
温馨提示
- 1. 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
- 2. 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
- 3. 本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
- 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
- 5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
- 6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
- 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
最新文档
- 2025年服装销售店长工作方案
- 2025年幼儿园语言文字工作方案
- 2025年幼儿小班教学老师工作方案
- 2025年电子自动血球分析装置项目可行性研究报告
- 《自由落体运动》教学设计
- 2025年生肖牛浮雕项目可行性研究报告
- 2025年特润嫩白面膜膏项目可行性研究报告
- 2025年燃油锅炉模糊控制系统项目可行性研究报告
- 山东铝业职业学院《组织行为学》2023-2024学年第二学期期末试卷
- 日照市重点中学2024-2025学年高三年级下学期3月质量检测试题卷化学试题含解析
- 苏州市公安局招聘警务辅助人员笔试真题2024
- GA/T 1433-2017法庭科学语音同一认定技术规范
- 铁矿石外贸合同中英对照
- (整理)变频器电力电缆标准
- 《统计学》完整ppt课件(PPT 228页)
- 人力资源部岗位廉洁风险点及防范措施
- 求一个数比另一个数多几少几应用题
- 公路工程全过程跟踪审计服务方案
- 华南师范大学论文论文封面
- 五年级冀教版英语下册按要求写句子专项习题
- 中英文验货报告模板

评论
0/150
提交评论