空间几何体的计算

1、空间几何体的计算一、柱、锥、台体的计算例1： 已知棱长为a，各面均为等边三角形的四面体SABC，求它的表面积.变式训练1.已知圆柱和圆锥的高、底面半径均分别相等.若圆柱的底面半径为r，圆柱侧面积为S，求圆锥的侧面积.2.两个平行于圆锥底面的平面将圆锥的高分成相等的三段，那么圆锥被分成的三部分的体积的比是_3.三棱锥VABC的中截面是A1B1C1，则三棱锥VA1B1C1与三棱锥AA1BC的体积之比是_例2： 有位油漆工用一把长度为50 cm，横截面半径为10 cm的圆柱形刷子给一块面积为10 m2的木板涂油漆，且圆柱形刷子以每秒5周的速度在木板上匀速滚动前进，则油漆工完成任务所需的时间是多少?（

2、精确到0.01秒）变式训练:已知三棱锥OABC中，OA、OB、OC两两垂直，OC=1,OA=x，OB=y，且x+y=4，则三棱锥体积的最大值是_.例3： 有一堆规格相同的铁制（铁的密度是7.8 g/cm3）六角螺帽,共重5.8 kg,已知底面是正六边形，边长为12 mm,内孔直径为10 mm,高为10 mm，问这堆螺帽大约有多少个?（取3.14）变式训练:如图，有个水平放置圆台形容器，上、下底面半径分别为2分米，4分米，高为5分米，现以每秒3立方分米的速度往容器里面注水，当水面的高度为3分米时，求所用的时间.（精确到0.01秒）例4： 图中所示的几何体是一棱长为4 cm的正方体，若在它的各个面

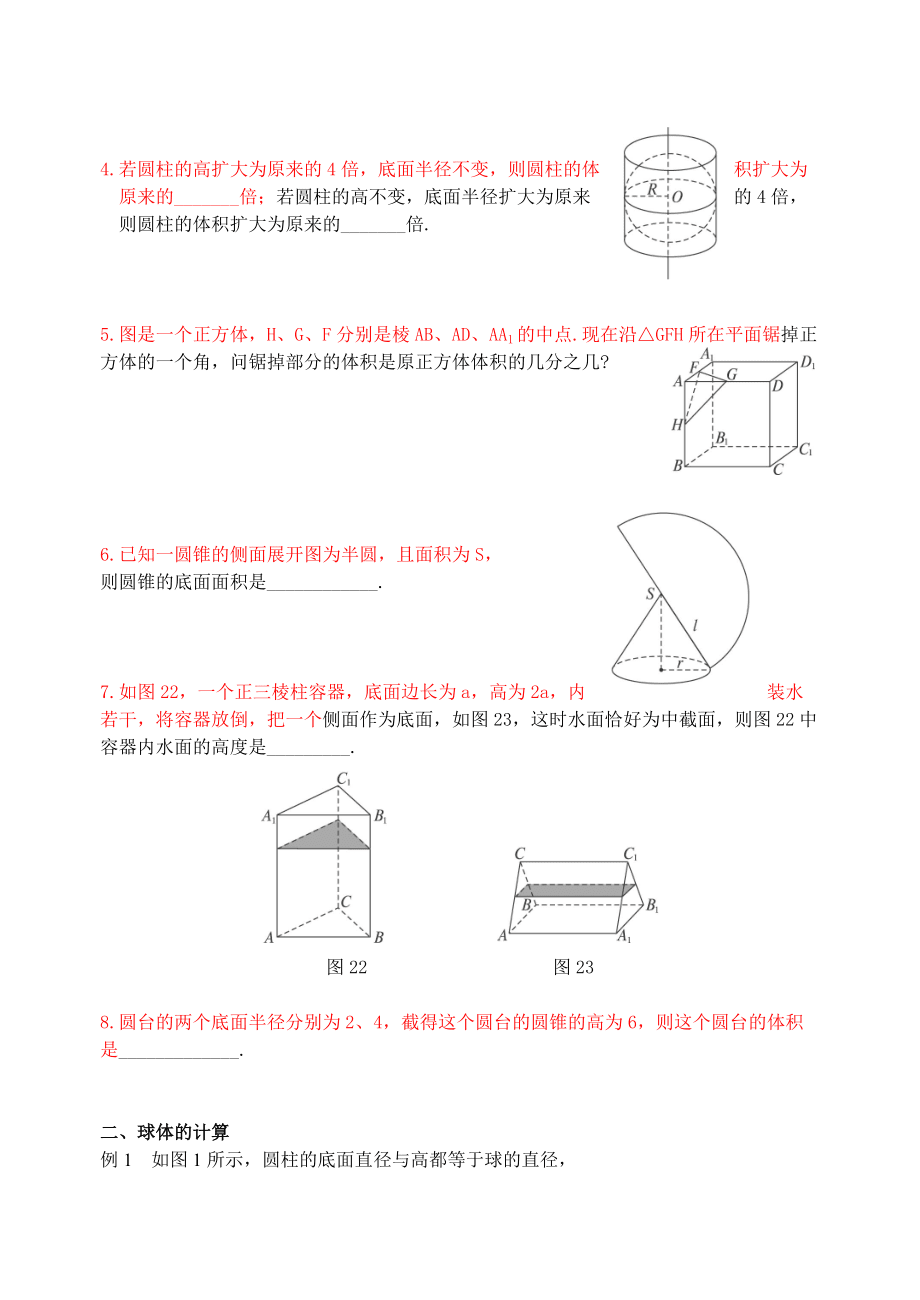
3、的中心位置上，各打一个直径为2 cm、深为1 cm的圆柱形的孔，求打孔后几何体的表面积是多少? 巩固训练：1.正方体的表面积是96，则正方体的体积是=_。2.如图19所示，圆锥的底面半径为1，高为，则圆锥的表面积为_3.正三棱锥的底面边长为3，侧棱长为，则这个正三棱锥的体积是_。4.若圆柱的高扩大为原来的4倍，底面半径不变，则圆柱的体积扩大为原来的_倍；若圆柱的高不变，底面半径扩大为原来的4倍，则圆柱的体积扩大为原来的_倍.5.图是一个正方体，H、G、F分别是棱AB、AD、AA1的中点.现在沿GFH所在平面锯掉正方体的一个角，问锯掉部分的体积是原正方体体积的几分之几?6.已知一圆锥的侧面展开图

4、为半圆，且面积为S，则圆锥的底面面积是_.7.如图22，一个正三棱柱容器，底面边长为a，高为2a，内装水若干，将容器放倒，把一个侧面作为底面，如图23，这时水面恰好为中截面，则图22中容器内水面的高度是_. 图22 图238.圆台的两个底面半径分别为2、4，截得这个圆台的圆锥的高为6，则这个圆台的体积是_.二、球体的计算例1 如图1所示，圆柱的底面直径与高都等于球的直径，求证：（1）球的体积等于圆柱体积的；（2）球的表面积等于圆柱的侧面积.变式训练1.如图所示，表面积为324的球，其内接正四棱柱的高是14,求这个正四棱柱的表面积.2有一种空心钢球，质量为142 g,测得外径（直径）等于5 cm

5、，求它的内径（钢的密度为7.9 g/cm3，精确到0.1 cm）.例2 有一个轴截面为正三角形的圆锥容器，内放一个半径为R的内切球，然后将容器注满水，现把球从容器中取出，水不损耗，且取出球后水面与圆锥底面平行形成一圆台体，问容器中水的高度为多少？例3：若棱长为3的正方体的顶点都在同一球面上，则该球的表面积为_.变式训练1.已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是_2.若正四面体的棱长为a，则这个正四面体的外接球的体积为_.3.一个长方体的各顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为1,2,3，则此球的表面积为_.知能训练1.三个球的半径之比为123，那么最大球的表面积是其余两个球