工学项目5--弯曲构件力学分析

1、工学项目5弯曲构件力学分析 【知识目标】通过本工学项目的学习，理解平面弯曲的概念；掌握剪力图和弯矩图的绘制方法，尤其是简捷法；掌握弯曲构件横截面上应力的作用形式、分布规律；掌握弯曲构件的强度及刚度检算；理解影响线的概念并会绘制单跨静定梁的影响线，会确定移动荷载的最不利位置，会计算简支梁的跨中最大弯矩和绝对最大弯矩。 【能力目标】通过本工学项目的学习，能够检算单跨静定梁的强度、刚度；会确定移动荷载的最不利位置，会计算简支梁的跨中最大弯矩和绝对最大弯矩。教学安排表（推荐）如表5.1所示。 表5.1教学安排表（推荐） 内容序号 教学内容课时习题子项目1单跨静定梁的内力计算与内力图绘制8思5.15.5

2、、习5.15.3多跨静定梁的内力计算与内力图绘制2思5.6、习5.4梁的应力与强度计算8思5.75.15、习5.55.12子项目2梁的变形与刚度计算6习5.13子项目3梁在移动荷载作用下的内力计算6思5.165.20、习5.144.17子项目1概况：如图5.1所示的单跨静定梁在土木工程结构中普遍使用，它们要正常使用，必须有一定的承载能力，即必须满足强度、刚度要求。本项目主要研究这类单跨静定梁的强度问题。图5.1相关知识：5.1 单跨静定梁的内力计算与内力图绘制一、平面弯曲的概念杆件受到垂直于其轴线的外力或位于其轴线所在平面内的外力偶作用时，杆轴线由直线变为曲线的变形称为弯曲（图5.2），以弯曲

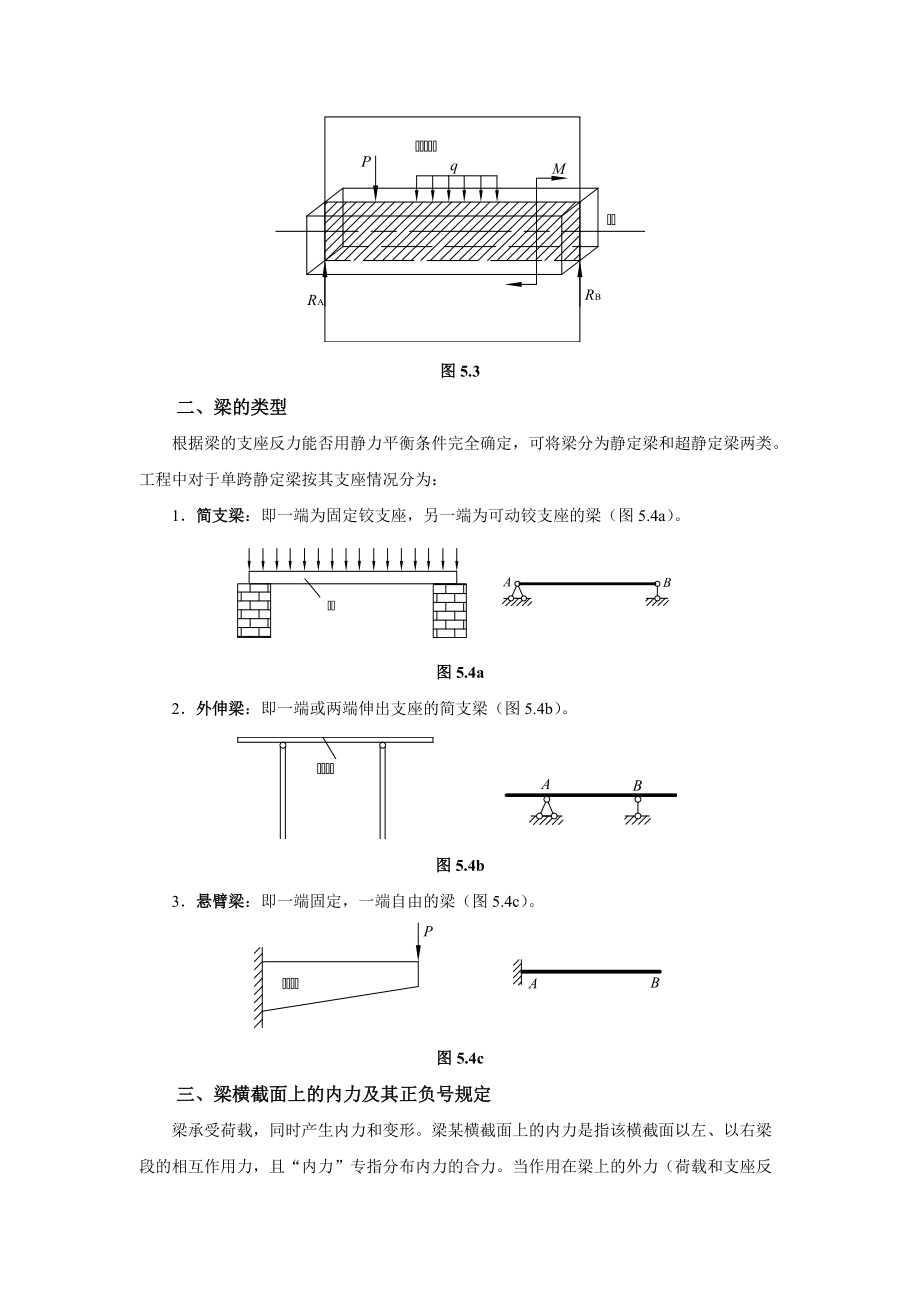
3、变形为主要变形形式的杆件称为梁。图5.2工程中常见的梁，其横截面往往有一根竖向对称轴，这根对称轴与梁轴线所组成的平面，称为纵向对称平面。当作用在梁上的外力和外力偶（包括荷载和支座反力）都位于纵向对称平面内时，梁的轴线将在此纵向对称平面内弯曲，如图5.3所示。这种弯曲平面与外力作用平面相重合的弯曲，称为平面弯曲。图5.3二、梁的类型根据梁的支座反力能否用静力平衡条件完全确定，可将梁分为静定梁和超静定梁两类。工程中对于单跨静定梁按其支座情况分为：1简支梁：即一端为固定铰支座，另一端为可动铰支座的梁（图5.4a）。图5.4a2外伸梁：即一端或两端伸出支座的简支梁（图5.4b）。图5.4b3悬臂梁：即

4、一端固定，一端自由的梁（图5.4c）。图5.4c三、梁横截面上的内力及其正负号规定梁承受荷载，同时产生内力和变形。梁某横截面上的内力是指该横截面以左、以右梁段的相互作用力，且“内力”专指分布内力的合力。当作用在梁上的外力（荷载和支座反力）已知时，用截面法即可显示和确定梁在某截面上的内力。1剪力和弯矩图5.5(a)所示的简支梁，其荷载和支座反力、是作用在该梁纵向对称平面内的平衡力系。在计算出、之后，利用截面法即可分析梁上任一横截面上的内力。假想沿截面将梁截为左右两段，取左段作为研究对象，由图5.5(b)可见，因有支座反力作用，为使左段平衡，截面上必有与反向的内力存在，于是由得：，相切于横截面的内

5、力，称为剪力，常用单位：牛（N）或千牛（kN）。同时，对截面的形心点有一个顺时针力矩，为满足左段平衡，截面也必然有一个与力矩转向相反的内力偶矩存在，于是由得：，作用面与横截面相垂直的内力偶矩，称为弯矩，常用单位：牛·米（N·m）、牛·毫米（N·mm）、千牛·米（kN·m）。图5.5若取右段梁作为研究对象，同样可计算出横截面上的和。根据作用力和反作用力的关系，右段梁在截面上的、与左段梁在同一截面上的、应该大小相等，方向（或转向）相反，如图5.5(c)所示。2剪力和弯矩的正、负号规定剪力符号：当截面上的剪力使分离体有顺时针方向转动的趋势时

6、为正，如图5.5(b)、(c)，反之为负。弯矩符号：当截面上的弯矩使分离体上部受压、下部受拉时为正，如图5.5(b)、(c)，反之为负。例5.1如图5.6(a)所示的简支梁，已知、。请计算截面上的剪力和弯矩。图5.6解：（1）计算支座反力以整梁为研究对象，假设支座反力、方向向上，列平衡方程：由得：，由得：（2）截面法计算内力知识链接截面法计算内力的步骤：截取代平截：假想在指定截面处将梁截成两段。取：取左段作为研究对象。代：在假想截面处代以剪力和弯矩，假定为正，画出研究对象的受力图（图5.6(b)）。平：列平衡方程求解。由得：由得：归纳总结截面法计算内力规律1（正负号）：（1）在画研究对象的受力

7、图时，Q、M按其正负规定，假定为正。（2）在列平衡方程时，把Q、M作为研究对象上的外力看待。注：若计算结果为正，说明假设方向与实际方向一致；若结果为负，说明假设方向与实际方向相反。假如取右段作为研究对象，并设剪力和弯矩都为正，画出研究对象的受力图（图5.6(c)），列平衡方程：由得：由得：可见，选取右段梁或选取左段梁为研究对象，所得截面上的内力结果相同。归纳总结截面法计算内力规律2：截面法计算内力时可取截面以左或以右部分作为研究对象，一般取外力较简单的一侧进行分析。例5.2如图5.7(a)所示的外伸梁，截面11和22都无限接近于截面B，截面 33和 44也都无限接近于截面C。请计算这些截面上的

8、剪力和弯矩。图5.7解：（1）计算支座反力以整梁为研究对象，假设支座反力、方向向上，列平衡方程：由得：由得：（2）取截面11左段作为研究对象，并设剪力和弯矩都为正，画出研究对象的受力图（图5.7(b)），列平衡方程：由得：，由得：，（3）取截面22左段作为研究对象，并设剪力和弯矩都为正，画出研究对象的受力图（图5.7(c)），列平衡方程：由得：，由得：，（4）取截面33右段作为研究对象，并设剪力和弯矩都为正，画出研究对象的受力图（图5.7(d)），列平衡方程：由得：，由得：（5）取截面44右段作为研究对象，并设剪力和弯矩都为正，画出研究对象的受力图（图5.7(e)），列平衡方程：由得：，由得：

9、归纳总结（1）在集中力的两侧截面：弯矩相同、剪力发生突变，突变值等于该集中力的大小。当集中力向上时，剪力图向上跳跃；反之，向下跳跃。（2）在集中力偶的两侧截面：剪力相同、弯矩发生突变，突变值等于该集中力偶力偶矩的大小。当集中力偶顺时针方向作用时，弯矩图向上跳跃，反之向下跳跃。自己动手做请用截面法计算图5.8所示简支梁指定截面上的剪力和弯矩。图5.8四、梁的内力图在梁的强度和刚度问题中，除要计算指定截面的剪力和弯矩外，还必须知道剪力和弯矩沿梁轴线的变化规律，从而找到梁内剪力和弯矩的最大值以及它们所在的截面位置。1函数法根据内力方程绘制内力图一般情况下，截面上的剪力和弯矩是随截面位置变化的，若横截

10、面的位置用沿梁轴线的坐标x表示，则各个横截面上的剪力和弯矩都可以表示为坐标x的函数，即：和分别称为剪力方程和弯矩方程，它们可以表明梁内剪力和弯矩沿梁轴线的变化规律。为了能形象地表现剪力和弯矩沿梁轴线的变化规律，可以根据剪力方程和弯矩方程分别绘制剪力图和弯矩图。其绘制方法与轴力图相似，以沿梁轴线的横坐标x表示梁横截面的位置，以纵坐标表示相应截面的剪力或弯矩。一般认为，剪力Q坐标轴向上为正，弯矩M坐标轴向下为正。例5.3 请用函数法绘制图5.9(a)所示简支梁的剪力图和弯矩图。图5.9解：（1）计算支座反力以整梁为研究对象，假设支座反力、方向向上，列平衡方程：由得：，由得：，（2）列剪力和弯矩方程

11、设梁的左端点A为坐标原点，在AC范围内，在距原点x截面处取左段梁为研究对象，列出剪力方程和弯矩方程： （） （） 在CB范围内，在距原点x截面处取左段梁为研究对象，列出剪力方程和弯矩方程： （） （） （3）绘制剪力图和弯矩图剪力图：在AC范围内，剪力Q（x）为常数，剪力图是在x轴上方平行于x轴的一条直线；在CB范围内，剪力Q（x）为常数，剪力图是在x轴下方平行于x轴的一条直线，绘制剪力图如图5.9(b)所示。弯矩图：在AC范围内，弯矩M（x）是x的一次函数，弯矩图是一条斜直线；在CB范围内，弯矩M（x）是x的一次函数，弯矩图是一条斜直线，绘制弯矩图如图5.9(c)所示。由内力图可知，受集中力

12、作用的简支梁，当ab时，最大剪力发生在CB段的任意截面上，其数值；最大弯矩发生在集中力作用处的截面上，其数值。如集中力作用在梁的跨中，即当a=b=l/2时，则最大弯矩发生在梁的跨中截面上，其数值。例5.4 请用函数法绘制图5.10(a)所示简支梁的剪力图和弯矩图。图5.10解：（1）计算支座反力以整梁为研究对象，由对称关系可得：（2）列剪力方程和弯矩方程设梁的左端点A为坐标原点，在距原点x截面处取左段梁为研究对象，列出剪力方程和弯矩方程： （） （） （3）绘制剪力图和弯矩图剪力图：剪力Q（x）是x的一次函数，剪力图是一条斜直线，绘制剪力图如图5.10b所示。弯矩图：弯矩M（x）是x的二次函数

13、，弯矩图是一条二次抛物线，绘制弯矩图如图5.10c所示。由内力图可知，受均布荷载作用的简支梁，最大剪力发生在梁端，其数值；最大弯矩发生在剪力为零的跨中截面，其数值。归纳总结剪力图、弯矩图图线类型：（1）无荷载区段：剪力图为水平线，弯矩图为斜直线。（2）均布荷载区段：剪力图为斜直线，弯矩图为二次抛物线。2简捷法根据微分关系绘制内力图如图5.11所示，梁上作用一分布荷载，荷载集度为的连续函数，并规定以向上为正。取A为坐标原点，x轴向右为正。图5.11无荷载的梁段，有。假想用截面和截取长为的微段作为分离体，其上荷载集度视为均布。设距离坐标原点x处的截面上的内力为和，距坐标原点的截面上的内力为、。因为

14、整梁平衡，因此微段也平衡。由得： 由此得到结论一：梁上任一横截面上的剪力对的一阶导数等于作用在该截面处的分布荷载集度。此微分关系的几何意义是：剪力图上某点切线的斜率等于相应截面处的分布荷载集度。对微段右侧截面的形心取矩，由得：略去二阶微量，得： 由此得到结论二：梁上任一横截面上的弯矩对的一阶导数等于该截面处的剪力。此微分关系的几何意义是：弯矩图上某点切线的斜率等于相应截面处的剪力。对上式两边求导，得： 由此得到结论三：梁上任一横截面上的弯矩对的二阶导数等于该截面处的分布荷载集度。此微分关系的几何意义是：弯矩图上某点的曲率等于相应截面处的分布荷载集度。由分布荷载集度的正负可以判断弯矩图的凸凹方向

15、。绘制剪力图和弯矩图的关键是确定图线的类型和位置。利用荷载集度、剪力和弯矩之间的微分关系来判断每一区段剪力图和弯矩图的图线类型（见表5.2），然后确定控制截面的剪力值和弯矩值，从而简便地绘制出内力图。这种方法称为简捷法。表5.2荷载、剪力图和弯矩图之间的关系内力图荷载Q图图线类型M图图线类型无荷载区段水平线（一点确定）斜直线（两点确定）注：Q为0时，为水平线。均布荷载区段斜直线（两点确定）二次抛物线（两点or三点确定）备注（1）关键点的位置：集中力的作用点；集中力偶的作用点；分布荷载的起点、终点；支座的位置、中间铰点。（2）剪力图中下一个关键点的纵坐标=上一个关键点的纵坐标+荷载图（即受力图）

16、中对应区段的面积；弯矩图中下一个关键点的纵坐标=上一个关键点的纵坐标+剪力图中对应区段的面积。例5.5请用简捷法绘制图5.12(a)所示简支梁的剪力图和弯矩图。Q图（kN）M图（kN·m）517108P=6KNq =3KN/mABCD2m2m2mRBRAa）b）c）图5.12解：（1）计算支座反力以整梁为研究对象，假设支座反力、方向向上，列平衡方程：由得：， 由得：， （2）绘前准备（画轴线、标关键点）根据梁上荷载情况，取A、B、C、D四个关键点绘制内力图。（3）绘图剪力图：对应荷载图中AB间面积为0，BC间面积为0，CD间面积为-6。表5.3剪力图区段荷载Q图图线类型Q值/ABq=

17、0水平线BCq=0水平线CDq=常数斜直线绘制剪力图如图5.12b所示。弯矩图：对应剪力图中AB间面积为10，BC间面积为-2，CD间面积为-8。表5.4弯矩图区段剪力M图图线类型M值/ ABQ=常数斜直线BCQ=常数斜直线CDQ=变量曲线绘制弯矩图如图5.12c所示。（4）绘后完善（标数值、画竖标线、标正负号、标图名、标单位、标斜交点）归纳总结简捷法绘制内力图的主要步骤：2+1+6=9步绘前准备画轴线标关键点+绘图+绘后完善标数值画竖标线标正负号标图名标单位标斜交点例5.6请用简捷法绘制图5.13(a)所示外伸梁的剪力图和弯矩图。图5.13解：（1）计算支座反力以整梁为研究对象，假设支座反力

18、、方向向上，列平衡方程：由得：，由得：，（2）绘前准备（画轴线、标关键点）根据梁上荷载情况，取A、B、C三个关键点绘制内力图。（3）绘图剪力图：对应荷载图中AB间面积为-40， BC间面积为0。表5.5剪力图区段荷载Q图图线类型Q值/ABq=常数斜直线BCq=0水平线绘制剪力图如图5.13(b)所示。弯矩图：附加关键点D，对应剪力图中AD间面积为5，DB间面积为-45，BC间面积为40。特别注意注：若剪力图上图线与轴线斜交，则在绘制弯矩图时需在该对应位置附加关键点。表5.6弯矩图区段剪力M图图线类型M值/ ABQ=变量曲线BCQ=常数斜直线绘制弯矩图如图5.13c所示。（4）绘后完善（标数值、

19、画竖标线、标正负号、标图名、标单位、标斜交点）例5.7请用简捷法绘制图5.14(a)所示简支梁的剪力图和弯矩图。RBRAM图（）Q图（）图5.14解：（1）计算支座反力以整梁为研究对象，由对称关系可得： （2）绘前准备（画轴线、标关键点）根据梁上荷载情况，取A、C、D、B四个关键点绘制内力图。（3）绘图剪力图：对应荷载图中AC间面积为-4，CD间面积为-32，DB间面积为-4。表5.7剪力图区段荷载Q图图线类型Q值/ACq=常数斜直线CDq=常数斜直线DBq=常数斜直线绘制剪力图如图5.14(b)所示。弯矩图：附加关键点E，对应剪力图中AC间面积为43.6，CE间面积为6.4，ED间面积为-6

20、.4，DB间面积为-43.6。表5.8弯矩图区段剪力M图图线类型M值/ ACQ=变量曲线CDQ=变量曲线DBQ=变量曲线绘制弯矩图如图5.14(c)所示。（4）绘后完善（标数值、画竖标线、标正负号、标图名、标单位、标斜交点）自己动手做请用简捷法绘制图5.15所示各梁的剪力图和弯矩图。a）b）图5.153叠加法根据叠加原理绘制内力图在工程实际中，梁的变形为小变形。在计算支座反力、剪力和弯矩时，均忽略微小变形量的影响，而按照原始尺寸计算，所得到的结果均与梁上荷载成线性关系（见表5.9）。在这种情况下，如果梁上同时有几项荷载作用，如图5.16(a)所示，那么每项荷载所引起的支反力、内力不会受其它荷载

21、作用的影响。这样，就可以分别计算各项荷载单独作用时梁的某一量值（例如同一支座的同一种支反力，或同一截面的同一种内力），再求它们的代数和，即得几项荷载共同作用下的该量值。例如图5.16所示悬臂梁，有：，。图5.16这里实际应用了一个带有普遍性的原理，即叠加原理：在几个荷载共同作用下所引起的某一量值（支反力、内力、应力或位移），等于各个荷载单独作用时所引起的该量值的代数和。表5.9 简单梁在单一荷载作用下的弯矩图根据叠加原理来绘制内力图的方法称叠加法。在常见荷载作用下，梁的剪力图比较简单，一般不用叠加法绘制。以下只讨论用叠加法画弯矩图。如图5.16(a)所示，对于指定截面C的弯矩叠加，是指弯矩图C

22、截面处纵标线（有向线段）的叠加：设图5.16(b)中表示的ji为第一条纵表标线，图5.16(c)中表示的ih为第二条纵表标线，现以第一条纵标线的终点作为第二条纵标线的起点，按前者方向连接第二条纵标线，形成表示的纵标线jh，如图5.16(a)所示。若所有截面上的弯矩进行叠加，则为各截面处弯矩图纵标线同时各自叠加，因为图5.16(c)中的所有纵标线的起点都要落在图5.16(b)的图线上，所以图5.16(c)的弯矩图作了相应的错动（如图5.16(c)上方的虚线范围）。错动的前提条件是：图形在垂直于杆轴线的方向错动；错动前后面积不变；其形心沿杆轴线方向的坐标不变。例5.8 请用叠加法绘制图5.17所示

23、简支梁的弯矩图。图5.17分析：将集中力偶、均布荷载分别单独作用在梁上，绘制弯矩图。在直线图形（图5.17(b)）上叠加曲线图形，即将曲线图形错动，使其基线平行于直线图形的图线，如图5.17(c)，再让这两条平行线段重合。作图：绘制简支梁在集中力偶作用下的弯矩图。图线画虚线，如图5.17(a)所示。以这条图线为基线绘制梁在均布荷载作用下的弯矩图，纵标线始终垂直于梁的轴线。以第一图形的基线为基线，第二图形的图线为图线，所形成的图形即为所求的弯矩图，如图5.17(a)。例5.9 请用叠加法绘制图5.18(a)所示外伸梁的弯矩图。图5.18分析：先绘制均布荷载单独作用在BD段梁上的弯矩图，得到B点弯

24、矩为。然后再考虑AB段的弯矩叠加。作图：AB段简支梁段的图线为斜直线，用虚线表示。以此条图线为基线，绘制集中力作用下的弯矩图，简支段弯矩图为三角形，集中力处的弯矩值为。以第一图形的图线为基线，第二图形的图线为图线，形成的图形即为所求的弯矩图，如图5.18(b)。5.2多跨静定梁的内力计算与内力图绘制一、多跨静定梁的组成单跨静定梁多使用于跨度不大的情况，如门窗、楼板、屋面大梁、短跨的桥梁以及吊车梁等。通常将若干根单跨梁用铰相连，并用若干支座与基础连接而组成的静定结构称为多跨静定梁。如图5. 19(a)所示为房屋建筑中一木檩条的结构图，在各短梁的接头处采用斜搭接加螺栓系紧。由于接头处不能抵抗弯矩，

25、因而视为铰结点。其计算简图如图5. 19(b)所示。从几何组成上看，多跨静定梁的组成部分可分为基本部分和附属部分。如图5. 19(b)所示，其中梁AB部分，有三根支座链杆直接与基础（屋架）相连，不依赖其它部分构成几何不变体系，称为基本部分；对于梁的EF和IJ部分，因它们在竖向荷载作用下，也能独立保持平衡，故在竖向荷载作用下，可以把它们当作基本部分；而短梁CD和GH两部分支承在基本部分之上，需依靠基本部分才能保持其几何不变性，故称为附属部分。为了清楚地看到梁各部分之间的依存关系和力的传递层次，可以把基本部分画在下层，把附属部分画在上层，如图5.19(c)所示，称为层次图。图5.19二、多跨静定梁

26、的内力计算从受力分析看，由于基本部分能独立地承受荷载而维持平衡，故当荷载作用于基本部分时，由平衡条件可知，将只有基本部分受力，附属部分不受力。而当荷载作用于附属部分时，则不仅附属部分受力，其反力将通过铰结处传给基本部分，使基本部分同时受力。由上述基本部分和附属部分力的传递关系可知，多跨静定梁的计算顺序应该是先计算附属部分，后计算基本部分。计算附属部分时，应先从附属程度最高的部分算起；计算基本部分时，把计算出的附属部分的约束力反其方向，作为荷载作用于基本部分。多跨静定梁中每一跨梁都是单跨梁，将各单跨梁的内力图连在一起，就是多跨静定梁的内力图。例5.10请绘制图5.20(a)所示多跨静定梁的剪力图

27、和弯矩图。图5.20解：（1）画出该多跨静定梁的层次图如图5.20(b)所示。（2）计算支座反力对梁列平衡方程可得：，将反方向作用于梁上，对梁列平衡方程可得： ，（逆时针）（3）绘制内力图分段绘制出各段梁的弯矩图和剪力图，连成一体即得多跨静定梁的弯矩图和剪力图，如图5.20(d)、(e)所示。例5.11请绘制图5.21(a)所示多跨静定梁的剪力图和弯矩图。图5.21解：（1）画出该多跨静定梁的层次图如图5.21(b)所示。（2）计算支座反力对梁列平衡方程可得：将反方向作用于梁上，对梁列平衡方程可得： 同理， （3）绘制内力图分段绘制出各段梁的弯矩图和剪力图，连成一体即得多跨静定梁的弯矩图和剪力

28、图，如图5.21(d)、(e)所示。归纳总结多跨静定梁内力计算的一般步骤：（1）对结构进行几何组成分析，弄清结构的几何组成顺序并画出结构层次图，先组成的部分（基本部分）画在下面，后组成的部分（附属部分）画在上面。（2）画出由结构层次图所确定的各单跨静定梁的受力图，并计算出各支座的约束反力。（3）取相同的比例尺，在同一直线上绘制出各跨梁的剪力图和弯矩图。自己动手做请绘制图5.22所示多跨静定梁的剪力图和弯矩图。 图5.22特别注意力的传递类似于水流，从上往下，即该力从所在部分向下一直传递到基本部分，而不会传递到上一层。注：若集中力作用在节点上，则该力应看作作用在该节点所连部分层次较低的一层上。5

29、.3梁的应力与强度计算一、梁横截面上的正应力特别注意弯曲构件横截面上的应力：（1）剪力Q剪应力（沿截面切线方向的应力分量）（2）弯矩M正应力（沿截面法线方向的应力分量）研究方法：（1）平面弯曲时横截面纯弯曲（横截面上只有M而无Q的情况）（2）平面弯曲时横截面横力弯曲（横截面上既有M又有Q的情况）1纯弯曲时的正应力如图5.23(a)所示的简支梁，荷载与支座反力都作用在梁的纵向对称平面内，其剪力图和弯矩图如图5.23(b)、(c)所示。在梁的AC和DB段中，各横截面上同时有剪力和弯矩，这种弯曲称为剪力弯曲或横力弯曲。在CD段中，各横截面上只有弯矩而无剪力，这种弯曲称为纯弯曲。图5.23为了使问题简

30、单，现以矩形截面梁为例，推导梁在纯弯曲时横截面上的正应力，从几何变形、物理关系和静力学关系等三方面考虑。（1）几何变形图5.24为观察梁纯弯曲时的表面变形情况，在矩形截面梁的表面画上一些纵向直线和横向直线，形成许多小矩形，然后在梁两端对称位置上加集中荷载P，梁受力后产生对称变形，在两个集中荷载之间的区段产生纯弯曲变形，如图5.24所示。从实验中观察到如下现象：所有纵向直线均变为曲线，靠近顶面（凹边）的纵向线缩短，靠近底面（凸边）的纵向线伸长，如图5.24(b)中的ii和jj。所有横向直线仍为直线，只是各横向线之间作了相对转动，但仍与变形后的纵向线正交, 如图5.24b中的mm。变形后横截面的高

31、度不变，而宽度在纵向线伸长区减小，在纵向线缩短区增大，如图5.24(b0右所示。根据以上观察到的现象，并将表面横向直线看作梁的横截面，可作如下假设：平面假设：变形前为平面的横截面，变形后仍为平面，它像刚性平面一样绕某轴旋转了一个角度，但仍垂直于梁变形后的轴线。单向受力假设：认为梁由无数微纵向纤维组成，各纵向纤维的变形只是简单的拉伸或压缩，各纵向纤维无挤压现象。根据平面假设，梁变形后的横截面转动，使得梁的凸边纤维伸长，凹边纤维缩短。由变形的连续性可知，中间必有一层纤维既不伸长也不缩短，此层纤维称为中性层，如图5.24d所示。中性层与横截面的交线称为中性轴（图5.25(d)），它将横截面分为受拉和

32、受压两个区域。在图示平面弯曲情况下的梁，由于外力作用在梁的纵向对称平面内，故梁的变形也对称于此平面，因此，中性轴应垂直于截面的对称轴。简而言之，在纯弯曲条件下，梁的各横截面仍保持平面并绕中性轴作相对转动，各纵向纤维处于纵向拉伸（压缩）状态。根据上述假设，由几何关系可推求出横截面上任一点处纵向纤维的线应变，从而找出纵向线应变的变化规律。为此，在梁上截取一微分段dx进行分析，如图5.25所示。图5.25设中性轴为坐标轴z，截面的对称轴为y，向下为正。现分析距中性层y处的纵向纤维ab的线应变。梁变形后截面mm、nn之间的相对转角为，纤维ab由直线变成弧线，O为中性层的曲线中心，为其曲率半径，则纤维a

33、b的纵向变形为：纤维ab的纵向线应变为： （5.1）对于确定的截面来说，是常量。因此该式表明，同一横截面上各点处的纵向线应变与该点到中性轴的距离y成正比。（2）物理关系由于假设纵向纤维只受单向拉伸或压缩，若正应力未超过材料的比例极限，由胡克定律可得： （5.2）这就是横截面上正应力变化规律的表达式。对于确定的截面来说，和均为常量。该式表明，梁横截面上的正应力沿截面高度呈线性分布，并以中性轴为界，一侧为拉应力，另一侧为压应力。中性轴处正应力为零；在距中性轴等远的各点处（同一层）的正应力相等；在截面的上、下边缘将产生正应力的最大值或最小值。这一变化规律如图5.26所示。y图5.26（3）静力学关系

34、式（5.2）只给出了正应力的分布规律，还不能用来计算正应力的数值。因为中性轴的位置尚未确定，曲率半径的大小也未知。为此我们利用静力学关系来解决这些问题。图5.27纯弯曲的梁，其横截面上的内力只有弯矩，如图5.27所示、在横截面上坐标y、z处取微面积dA，其上微内力为。由于横截面上的内力是所有微内力的合成，因此有： （5.3） （5.4）把式（5.2）代入式（5.3）得：因为，所以一定有：上式表明横截面对中性轴的静矩必须等于零。因此，直梁弯曲时中性轴必定通过截面的形心。把式（5.2）代入式（5.4）得：， （5.5）式（5.5）为中性层的曲率表达式，是弯曲理论中的一个重要公式，它反映了梁的变形程

35、度。式中称为梁的抗弯刚度。在弯矩相同的情况下，愈大，曲率就愈小。反映了梁截面抵抗弯曲变形的能力。将式（5.5）代回到式（5.2），便可得到梁纯弯曲时的正应力计算公式： （5.6）式（5.6）表明，梁在纯弯曲时横截面上任一点的正应力，与截面上的弯矩和该点到中性轴的距离成正比，而与截面对中性轴的惯性矩成反比。特别注意应用式（5.6）时，常以和的绝对值代入计算公式，并根据梁的变形情况直接判断的符号：即以中性轴为界，在受拉区的为正（拉应力），在受压区的为负（压应力），并将正负号写在计算式的前面。例5.12如图5.28所示的简支梁，已知，梁的跨度为3m，截面为矩形，。请计算：（1）C截面上a、b、c三点

36、处的正应力（2）梁的最大正应力及其位置图5.28解：（1）C截面上a、b、c三点处的正应力以整梁为研究对象，由对称关系可得：计算C截面的弯矩：计算截面对中性轴z的惯性矩：（压）（拉）（拉）（2）梁的最大正应力及其位置最大弯矩发生在跨中截面：由梁的变形情况可以判断：最大拉应力发生在跨中截面的下边缘处；最大压应力发生在跨中截面的上边缘处。最大正应力的值为： 2横力弯曲时的正应力前面所述式（5.6）是梁在纯弯曲条件下建立的，此时截面上只有弯矩而没有剪力。但常见的情况是，梁在横向力的作用下，截面上既有弯矩又有剪力。因此，杆件的横截面上不仅存在正应力，而且还有剪应力。由于剪应力的存在，杆件的横截面将发生

37、翘曲。此外，在与中性层平行的纵向截面上，还有横向力引起的相互挤压应力。这样，杆件在纯弯曲时所作的平面假设和纵向纤维之间互不挤压的假设将不能成立。但精确分析证明，当梁的跨度与截面高度之比lh5时，剪力的影响很小，例如均布荷载作用下的简支梁，当lh5时，横截面上的最大正应力按（5.6）式计算，其误差不超过1，符合工程中对精度要求。工程中梁的跨度远远大于横截面的高度，因此仍可以用式（5.6）计算横力弯曲时横截面上的正应力。此外，式（5.6）是以矩形截面梁在纯弯曲情况下推导出的，由于在推导过程中并未用到矩形的几何特征，故该公式也适用于具有纵向对称轴的其他形状截面的杆件，如圆形、工字形和T形截面。式（5

38、.6）是在直杆条件下推导的，一般不能用于曲杆。但对 R0y010的小曲率曲杆，如图5.29所示，其弯曲正应力也可近似地用式（5.6）计算。这里R0为曲杆轴线的原始曲率半径，y0 为截面形心到截面内侧边缘的距离。图5.293最大正应力产生最大正应力的截面，称为危险截面。对于等直梁，弯矩最大的截面就是危险截面。危险截面上的最大应力处称为危险点，它发生在距中性轴最远的上、下边缘处。对于中性轴是截面对称轴的梁，最大正应力的值为：令，则式中称为抗弯截面系数，是一个与截面形状和尺寸有关的几何量。常用单位是m3或mm3。值越大，就越小，它也反映了截面形状及尺寸对梁的强度的影响。对高为h、宽为b的矩形截面，其

39、抗弯截面系数为：对直径为d的圆形截面，其抗弯截面系数为：对于中性轴不是截面对称轴的梁，例如图5.30所示的T形截面梁，在正弯矩M作用下梁下边缘处产生最大拉应力，上边缘处产生最大压应力，其值分别为：令、，则有：图5.30二、梁横截面上的剪应力在横力弯曲情况下，梁的横截面上同时有弯矩和剪力存在，因此，横截面上不仅有与弯矩对应的正应力，还有与剪力对应的剪应力，但在一般情况下，剪应力是影响梁强度的次要因素，在此主要研究直梁横截面上剪应力的分布规律及大小计算。1矩形截面梁横截面上的剪应力在梁的横截面上，为了简化计算，在推导剪应力计算公式时，根据剪应力互等定理和截面上剪力是由切向分布内力合成所得，对狭长矩

40、形截面梁横截面上剪应力分布规律作如下假设（如图5.31所示）：（1）截面上各点处的剪应力的方向与剪力方向一致，并平行于两侧边。（2）横截面上距中性轴等远的各点处的剪应力大小相等。即剪应力沿截面宽度方向均匀分布。图5.31利用静力平衡条件可得到剪应力的大小为（推导过程略）： （5.7）式中： 一横截面上的剪力；横截面上需计算剪应力处的水平线以下（或以上）部分面积对中性轴的静矩；一横截面对中性轴的惯性矩；一矩形截面宽度。计算时、均为绝对值代入公式。当横截面给定时，、均为确定值，只有静矩随剪应力计算点在截面上的位置而变化。如图5.33(a)所示，对于矩形截面中的任意一点K点有：把上式及代入（5.7）

41、得：可见，剪应力的大小沿横截面的高度按二次抛物线规律分布，如图5.32(b)所示。在截面上、下边缘处（y =±h/2），剪应力为零；在中性轴处（y = 0），剪应力最大，其值为：可见，矩形截面梁横截面上的最大剪应力值是平均剪应力的1.5倍，发生在中性轴上。图5.322工字形截面梁横截面上的剪应力工字形截面由上下翼缘和腹板组成，如图5.33(a)。由于腹板是一狭长矩形，对矩形截面剪应力所作的假设仍然适用，所以腹板上任一点K（距中性轴y处）处剪应力可用公式（5.7）计算，即：式中： 一腹板的宽度；一图5.33(a)中阴影部分面积对中性轴的静矩。在腹板的范围内，是y的二次函数，故腹板部分的

42、剪应力沿腹板高度仍按二次抛物线规律变化，剪应力分布图如图5.33(b)所示，腹板上的最大切应力仍产生在中性轴的各点上。工字形截面翼缘上剪应力的情况较为复杂，且数值较小，一般不予计算。可以证明，工字形截面梁的最大剪应力仍发生在截面的中性轴处，其值为：。式中： 一半个截面（包括翼缘部分）对中性轴的静矩。图5.333圆形截面梁横截面上的剪应力y图5.34圆形截面的最大竖向剪应力也发生在中性轴上，并沿中性轴均匀分布，如图5.34所示，其值为：可见，在圆形截面梁横截面上的最大剪应力值是平均剪应力的1.33倍。三、梁的强度计算为了保证梁能安全地工作，必须使梁横截面上的最大应力不超过材料的许用应力。（1）正

43、应力强度条件为：式中：一材料许用正应力。（2）剪应力强度条件为：式中： 一材料许用剪应力。根据强度条件可解决有关强度方面的三类问题：（1）校核强度：已知梁的材料和横截面的形状、尺寸（即已知、b）以及所受荷载（即已知、），检查梁是否满足正应力、剪应力强度条件。（2）设计截面：已知所受荷载和梁的材料（即已知、），根据正应力强度条件计算出梁所需的最小抗弯截面系数，即然后根据梁的截面形状进一步确定截面的具体尺寸，最后校核其剪应力强度条件。（3）确定许用荷载：已知梁的材料和截面形状、尺寸（即已知、），根据强度条件计算出梁所能承受的最大弯矩，即然后由与荷载间的关系确定许用荷载，最后校核其剪应力强度条件。在

44、梁的强度计算中，必须同时满足正应力和剪应力两个强度条件。由于梁的强度多由正应力控制，所以通常是先按正应力强度条件设计截面或确定许用荷载，再用剪应力强度条件进行校核。一般情况下，当正应力强度满足时，剪应力强度也同时满足，不必进行剪应力强度校核。但当梁出现下列情况之一时，必须校核剪应力强度：（1）当梁的跨度较小或者在支座附近作用有较大荷载时，梁内可能出现弯矩较小而剪力很大的情况。（2）对于某些组合截面梁（如焊接的工字形钢板梁），当腹板厚度与其高度之比小于相应型钢的相应比值时。（3）木梁或玻璃钢等复合材料梁，由于材料的抗剪能力差，在横力弯曲时可能发生剪切破坏。例5.13如图5.35(a)所示的矩形截

45、面简支梁，已知材料的许用应力，。请校核该梁的强度。a）zA30020010kN/m4mBA20kN20kNb）c）图5.35解：（1）绘出剪力图、弯矩图（图5.35(b)、(c)），可见，。（2）校核强度C截面的最大压应力在上边缘点处，最大拉应力在下边缘点处，其值为：最大剪应力值为：故满足强度要求。特别注意使用正应力公式对梁进行强度计算时必须弄清所要计算的是哪个截面上、哪一点的正应力。例5.14如图5.36(a)所示的简支梁，已知，材料的许用应力。请选择工字钢的型号。图5.36解：（1）绘出弯矩图（图5.36(b)），可见C截面有最大正弯矩。（2）选择工字钢的型号由得每根工字梁所需的抗弯截面系

46、数为：由型钢表查得22a工字钢的，采用两根22a工字钢。例5.15如图5.37(a)所示的悬臂梁，已知该梁由两根不等边角钢2×125×80×10组成，材料的许用应力。请确定许用荷载。图5.37解：（1）绘出弯矩图（图5.37(b)），可见A截面有最大负弯矩。（2）计算许用荷载由得由型钢表查得125×80×10的抗弯截面系数为：故任务实施如图5.38(a)所示的工字钢简支梁，已知材料的许用应力，。请选择工字钢的型号。图5.38解：（1）绘出剪力图、弯矩图（图5.38(b)、(c)），可见，。（2）选择工字钢的型号由得查型钢表，选用22b工字钢，。

47、（3）因为支座附近有较大的集中力作用，故应作剪应力强度校核。由表查得22b工字钢的，则：梁的剪应力不满足强度要求，应加大截面尺寸。现以25b工字钢进行试校核。由型钢表查得：，因，故该梁可采用25b工字钢。四、平面应力状态1应力状态的概念在讨论轴向拉（压）杆斜截面上的应力时，我们已经知道通过拉（压）杆内任一点处的斜截面上的应力是随着截面方位角的变化而变化的。等直梁弯曲时，梁横截面上各点处的正应力及剪应力随距截面中性轴的距离而变化。因此，为了解决构件的强度问题，就要知道受荷载作用后的构件，在哪一点处及过该点处的哪个方位的斜截面上的应力是最大的，并研究其破坏的原因。过杆件内一点的所有不同方位截面上在

48、该点处的应力情况，称为此点处的应力状态。如图5.39a所示，为研究梁在荷载作用下其横截面mm上A点处的应力情况，围绕该点取一个边长为微分量的正六面体为研究对象，这个微六面体称为单元体。在mm截面处截取微段长dx，然后在A点处用两相距为dy高的上下水平面和相距宽为dz的前后竖直平面相切割，取出单元体（又称微元体），如图5.39(b)所示。根据梁的M和Q图（图5.39(c)）可知，此单元体左侧截面上有受压的正应力和向上的切应力，由于梁在荷载作用下是平衡的，因而从其中取出的单元体也应平衡，则单元体右侧截面有受压的正应力和向下的切应力，根据剪应力互等定理得出上下水平面上的应力如图5.39(b)所示。当

49、前后垂直平面上的应力为零时的应力状态，称为平面应力状态，可用如图5.39(d)所示的平面图形表示。图5.392平面应力状态的分析方法应力状态的分析方法一般有两种：一种是解析法，另一种是图解法。（1）平面应力状态分析解析法从受力构件内取出一点，其平面应力状态的单元体如图5.40(a)所示。四个侧面上的应力为、和、。单元体前后两个面上的应力为零，可用如图5.40(b)所示的平面图形表示。图5.40现讨论图示单元体中任意斜截面ef上的应力。斜截面的方位角从截面（其法线与轴重合）量起，以逆时针转向为正。在间变化时，该斜截面（通常称为截面）就代表图中的所有截面。用截面法将单元体沿ef截开，取出 ecf

50、楔体为研究对象，如图5.40(c)所示。斜截面上的应力为和，设斜截面的面积为dA，则平面cf和ce的面积分别为和，如图5.40(d)所示。列平衡方程计算和。由得：（5.8）由得：（5.9）根据剪应力互等定理，并有三角函数关系：将上述三式代入（5.8）、（5.9）得： （5.10） （5.11）式（5.10）、（5.11）就是平面应力状态时计算过一点任一方位斜截面上的应力公式，它反映了斜截面上的应力随方位角的变化规律。例5.16如图5.41(a)所示的矩形截面简支梁，已知截面尺寸，。请计算距离支座0.5mm处截面上A点在斜截面mm上的应力。图5.41解：（1）计算距离支座0.5mm处截面上的剪力

51、和弯矩（2）计算截面上A点的正应力及剪应力 （3）计算斜截面mm上的应力 斜截面mm上的应力均为负值，说明正应力是压应力，剪应力的方向对单元体是逆时针方向错动的，如图5.41c所示。（2）平面应力状态分析图解法前面讨论了用解析法计算单元体内斜截面上的应力，下面将研究用图解法（应力圆法）计算单元体内任一斜截面上的应力。将式（5.10）改写为：把上式及式（5.11）各自平方相加，整理后得：上式为一圆的方程，在直角坐标系中，该方程代表圆心为（，0），半径为的圆。通常称这个圆为应力圆（或莫尔圆）。应力圆是根据单元体的x截面（以x轴为法线的面）和y截面（以y轴为法线的面）上已知的应力、画的。具体步骤为：

52、建立直角坐标系，选取比例尺；根据x截面上的、值在坐标系中定出点，根据 y截面上的、值在坐标系中定出点；以为直径画圆即得应力圆，如图5.42b所示。从图上不难证明，直径与轴的交点C即为圆心，其坐标为（，0），半径的大小为。所以按上述方法画出的圆确为式（5.10）（5.11）对应的图形。画出应力圆后，可用它来计算单元体内任一斜截面上的正应力和剪应力。应力圆上的点与单元体内某一个斜截面上的应力之间的关系如下：应力圆圆周上的某一点的坐标值（，）与单元体内某个斜截面上的应力值、一一对应。如图5.42b中的应力圆上的Dx点对应单元体的x平面，应力圆上的Dy点对应单元体的y平面，应力圆上的E点对应单元体上倾角为的斜截面。应力圆上点与点之间的关系对应单元体上面与面之间的关系。应力圆上两点间圆弧所对的圆心角为单元体中对应的两个截面所夹角度的两倍。如图5.42b中，应力圆上Dx和Dy两点间圆弧所对应的圆心角为180°，单元体中相对应的两个截面（x、y截面）所夹角度为90°，是两倍的关系，并且它们的转向相同。总之，应力圆圆周上某一点与单元体内斜截面上应力之间的关系为“点面对应、转向相同、夹角两倍”。图5.42例5.17如图5.43所示的某工字钢简支梁一点处的单元体，请用应力圆法计算时斜截面上的应力。图5.43解：建立直角坐标系，选取比例尺，以，在坐标系中