朝阳二模文科试题及答案

1、北京市朝阳区高三年级第二次综合练习2019.5（考试时间120分钟 满分150分）本试卷分为选择题（共 40分）和非选择题（共 110分）两部分第一部分（选择题共40 分）一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，选出符合题目要求的一项.1.已知集合Ax|x1 , B x|x(x 2) 0，则 AUB(A) x|x0(B)x|1x 2(C) x|1x 2x|x0 且 x 12.复数 i(1+i)的虚部为(A)1(B) 0(C)(D)3.已知aln3 , c Iog3 2，贝y a , b , c的大小关系是(A) c(B)(C) a(D)4.在数学史上，中外数

2、学家使用不同的方法对圆周率估算.根据德国数学家莱布尼茨在1674年给出的求的方法绘制的程序框图如图所示.执行该程序框图，输出 s的值为(B)(C)(D)835215304105进行了.已知平面向量a,b的夹角为纟壬且a 1, b3(B) 732，则 |a b6.(A) 3(C) 7(D) 77已知等差数列an首项为ai，公差d0.贝厂印忌厶成等比数列”是“ a(A)充分而不必要条件(B)必要而不充分条件(C)充要条件(D)既不充分也不必要条件7.已知函数f(x)2x,xX, xa'若函数f (x)存在零点，则实数a的取值范围是 a.8.(A)(C)在棱长为,0,1(B)0,(D)1,1

3、的正方体ABCD A1B1C1D1中，E,F分别为线段CD和AB,上的动点,满足CE AiF，则四边形DiFBE所围成的图形(如图所示阴影部分)分别在该正方体有公共顶点的三个面上的正投影的面积之和3A.有最小值-25B.有最大值29.10.C.为定值3D.为定值2AiBiD1hEC第二部分(非选择题 共110分)填空题：本大题共 6小题，每小题5分，共30分.把答案填在答题卡上函数f(x) 2sinxcosx cos2x的最小正周期为已知点M (1,2)在抛物线C : y22 Px(p 0)上，贝U p；点M到抛物线C的焦点的距离是11.圆C ：x2 (y 1)2 1上的点P到直线l : x

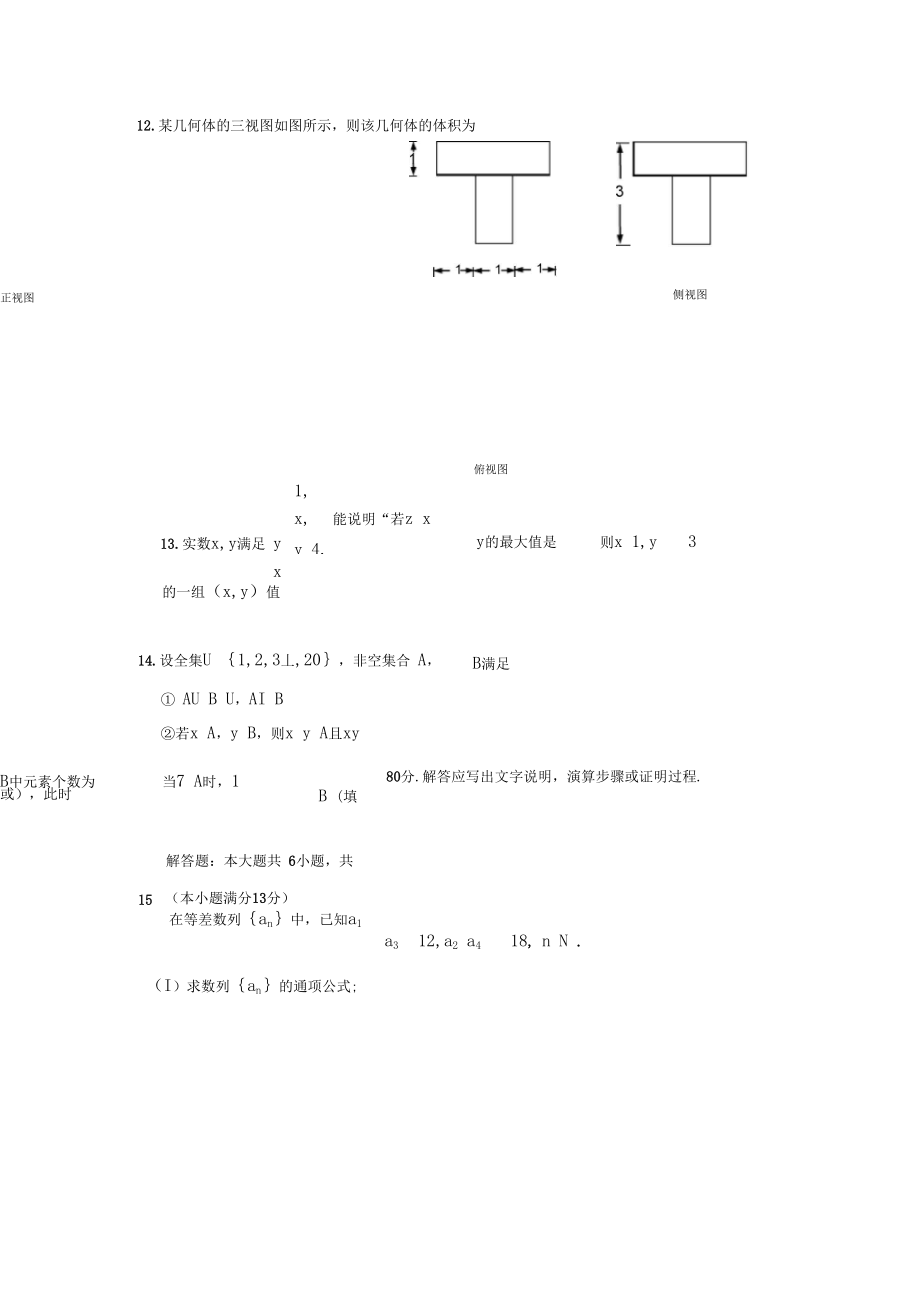
4、2y 3 0的距离的最小值是12.某几何体的三视图如图所示，则该几何体的体积为正视图侧视图俯视图13.实数x,y满足 yx1,x,能说明“若z xy 4.y的最大值是则x 1,y3 ”为假命题的一组（x,y）值是14.设全集U 1,2,3丄,20，非空集合 A，B满足以下条件: AU B U，AI B若x A，y B，则x y A且xy15.当7 A时，1B (填或），此时B中元素个数为解答题：本大题共 6小题，共80分.解答应写出文字说明，演算步骤或证明过程.（本小题满分13分）在等差数列an中，已知a1a312,a2 a418, n N .（I）求数列an的通项公式;(II )求 a3a6

5、a9.asn.16.(本小题满分13 分)如图，在四边形ABCD中， A 60 , ABC 90 .已知AD , BD .(I)求 sin ABD 的值;(n)若CD 2，且CD BC，求BC的长.CB17.(本小题满分13分)某电视台举行文艺比赛，并通过网络对比赛进行直播.比赛现场由5名专家组成评委给每位选手的最终得分需每位参赛选手评分，场外观众也可以通过网络给每位参赛选手评分要综合考虑专家评分和观众评分.某选手参与比赛后，现场专家评分情况如下表.另有约数万名场外观众参与评分，将观众评分按照7,8),8,9),9,10分组，绘成频率分布直方图如下专家ABCDE评分10108.88.99.7(

6、I)求a的值，并用频率估计概率,频率(n)从现场专家中随机抽取2人，求其中评分高于 9分的至少有1人的概率;(川)考虑以下两种方案来确定该选手的最终得分方案一：计算所有专家与观众评分的平均数x作为该选手的最终得分;方案二：分别计算专家评分的平均数x1和观众评分的平均数 x2，用凶一X2作为该2选手最终得分.请直接写出X与的大小关系-218.(本小题满分13分)如图1,在直角梯形ABCD 中，AB/DC , BAD 90°, AB4 , AD 2, DC 3,点E在CD上，且DE2，将 ADE沿AE折起，使得平面ADE平面ABCE (如图2).G为AE中点.(I)求证:DG 平面ABC

7、E ;(n)求四棱锥D ABCE的体积;(m)在线段BD上是否存在点 P ,使得CP/平面ADE ?若存在,求的值；若不存在,BD请说明理由.图1C图219.(本小题满分14 分)2y已知椭圆C : y21 (a>1)的离心率为a(I)求椭圆C的方程;(n)设直线I过点M (1,0)且与椭圆C相交于A, B两点.过点A作直线x 3的垂线，垂足为D .证明直线BD过x轴上的定点.20.(本小题满分14 分)已知函数f(x) (m 1)xIn x (m R).(I)当 m1时，求曲线yf (x)在(1,f(1)处的切线方程;(n)求函数f(x)的单调区间;(m)若函数g(x) 1x2+12

8、xf(x)在区间(1,2)内有且只有一个极值点，求m的取值范围.北京市朝阳区高三年级第二次综合练习数学（文）答案2019.5、选择题（40 分）题号12345678答案ACDCBCBD二、填空题（30分）题号91011121314答案2 ; 2亦19 -2（2,2）（答案不唯一）；18三、解答题（80 分）15.（本小题满分13分）解：（I）因为an是等差数列，a1a312,a2 a418,所以2a12a12d 12,4d 18.(II)则a316.解:解得 d3, al3 .则 an 3a3,a6,a9,., a3n 构成首项为(n 1) 3 3n,n N .a3=9，公差为9的等差数列.1

9、a6 a9 - a3n=9n 2n(n（本小题满分13分）(I)在 ABD中，由正弦定理，得.7分1)9 =9( n22ADsin ABDn).13分因为 A60 , AD所以sinABD詈sinA 书 sin60V6(n)由（I）可知,sinABD毎4BDsin ATo4.6分因为 ABC 90 ,所以 cos CBD cos(90ABD)sinABD逅4在BCD中，由余弦定理，得CD2BC22BD2 2BC BD cos CBD 因为 CD 2 , BD J6 ,所以 4 BC2 6 2BC J62即 BC 3BC 2=0 ,解得BC 1或BC 2 又 CD BC，则 BC 1 .13分1

10、7.（本小题满分13分）1.3分解：（I） a 0.3，某场外观众评分不小于 9的概率是丄2（n）设“从现场专家中随机抽取2人，其中评分高于9分的至少有1人”为事件Q-因为基本事件有AB， AC , AD，AE，BC，BD，BE，CD，CE，DE共10种，事件Q的对立事件只有CD 1 种,所以P(Q) 1910.9分（川）X2.13分1&（本小题满分13 分)解:（I）证明:因为G为AE中点,AD DE所以DGAE.因为平面ADE 平面ABCE ,C平面ADE I平面ABCE AE ,DG平面ADE ,.4分所以DG 平面ABCE （n）在直角三角形 ADE中，易求AE 2j2,则DG

11、 AD DE . AE所以四棱锥D ABCE的体积的体积为Vd abce 1血泸(m) 过点 C作 CF/AE 交 AB于点 F，贝U AF : FB 1:3 过点F作FP/AD交DB于点P，连接PC ,则DP: PB又因为CF/AE , AE 平面ADE , CF 平面 ADE ,所以CF/平面ADE .同理FP/平面ADE .又因为CF I PF F ,所以平面CFP/平面ADE .因为CP 平面CFP ,CB所以CP /平面ADE .BP所以在BD上存在点P ,使得CP/平面ADE，且一一BD.13分19.(本小题满分14分)(I)由题意可得 -a2a1,呢3b2解得1,爲.2所以椭圆C

12、的方程为31.4分(n)直线BD恒过x轴上的定点N (2,0) 证明如下(1) 当直线I斜率不存在时，直线I的方程为x 1 , 不妨设A(呼),B(1,刍，D(3,此时，直线BD的方程为：y2),所以直线BD过点(2,0).(2)当直线I的斜率存在时，设I :yk(x1)，A(X1, yj B(X2, y2), D(3, yj 由y由x2k(x3y2；得(3k21)x26k2x3k23 0.所以x1X2226k3k 32 , x1 x223k213k21直线BD（X 3），令y1(x2 3)y2 y1所以X3y2 3yi3yi所以f（X）的单调增区间为（0,） y2y13y2y2 y14x23

13、 X1X2X2 X1212k23k21X2 X1由于x1 x2，所以3k214x212k2可2.6k23k2 1故直线BD过点（2,0）.综上所述，直线 BD恒过X轴上的定点(2,0).14分20.（本小题满分14 分） 解：（I）当 m 1 时，f（X） 2x In所以 f(X)2 1 , f (1)X又 f(1)2 ,所以曲线y f（x）在（1,f（1）处的切线方程为3x y.4分(m 1)x 1X(n)函数f (x)的定义域为(0,) f (x) m 1(1)当 m 1 > 0即 m >1 时,因为 X （0,）时，f（X）0,所以(2)当 m 1丄时，fm 11时，f (x

14、)m 1f (x)的单调增区间为(x)(0,即m 1时，令f (x)0 ,-)，减区间为(,m 1m 1综上，当m >1时，f(x)的单调增区间为(0,)；当m 1时，f (x)的单调增区间为(0,1)，减区间为m 1.9分(川)因为 g(x) -x2 + 12(m1)xIn x,1所以 g (x) X p (mx1)令 h(x) x3 (m1)x2若函数g(x)在区间则函数h(x)在区间又 h(0)10所以h (x)在0,且 x 0,x0时,xxg,时,则 h(x)在 0,x0(m 1)x2 x1 , h (x) 3x22(m 1)x 1 .(1,2)内有且只有一个极值点，(1,2)内存在零点.内有唯一零点x0.h(x) 0;h(x) 0,内为减函数，在内为增函数.又因为h(0)10,且 h(x)在1,2内存在零点,所以h(1)h(2)0,0.解得2 m显然h(x)在1,2内有唯一零点,记为x-i.当 x1,X1 时，h(x) 0，xxi,2时，h