陕西省西安市八校2020届高三上学期期末考试数学(理)试卷

1、数学（理科）第I卷（选择题共60分）一、选择题：本大题共 12小题，每小题5分，在每小题给出的四个选项中，只有一项是符 合题目要求的.21.集合 M x|lgx 0, N x|x <4,则 m I N （）A. （ 2,0）B. 1,2） C. （1,2 D. （0, 2）为平面，若m ,np q2.3.4.(1i)zi （其中i为虚数单位）B. iC.2i d.2i已知命题p:若a|b | ,则a2 b2 ;命题q: m、皿直线,则mn下列命题为真命题的是（a. p q b. p q c.p q d.已知&为数列an的前n项和，Sn1斗，则&（A 31A .32c.32

2、c 31D.165.如图是某地区 2000年至2016年环境基础设施投资额 y （单位：亿元）的折线图.则下列结论中表述不正确的是（A.从2000年至2016年，该地区环境基础设施投资额逐年增加;B. 2011年该地区环境基础设施的投资额比2000年至2004年的投资总额还多；C. 2012年该地区基础设施的投资额比2004年的投资额翻了两番D.为了预测该地区2019年的环境基础设施投资额，根据 2010年至2016年的数据（时间变量t的值依次为1,2,，7）建立投资额y与时间t的线性回归模型 ? 99 17.5t,根据该模型预测该地区 2019的环境基础设施投资额为256.5亿元.ir _.

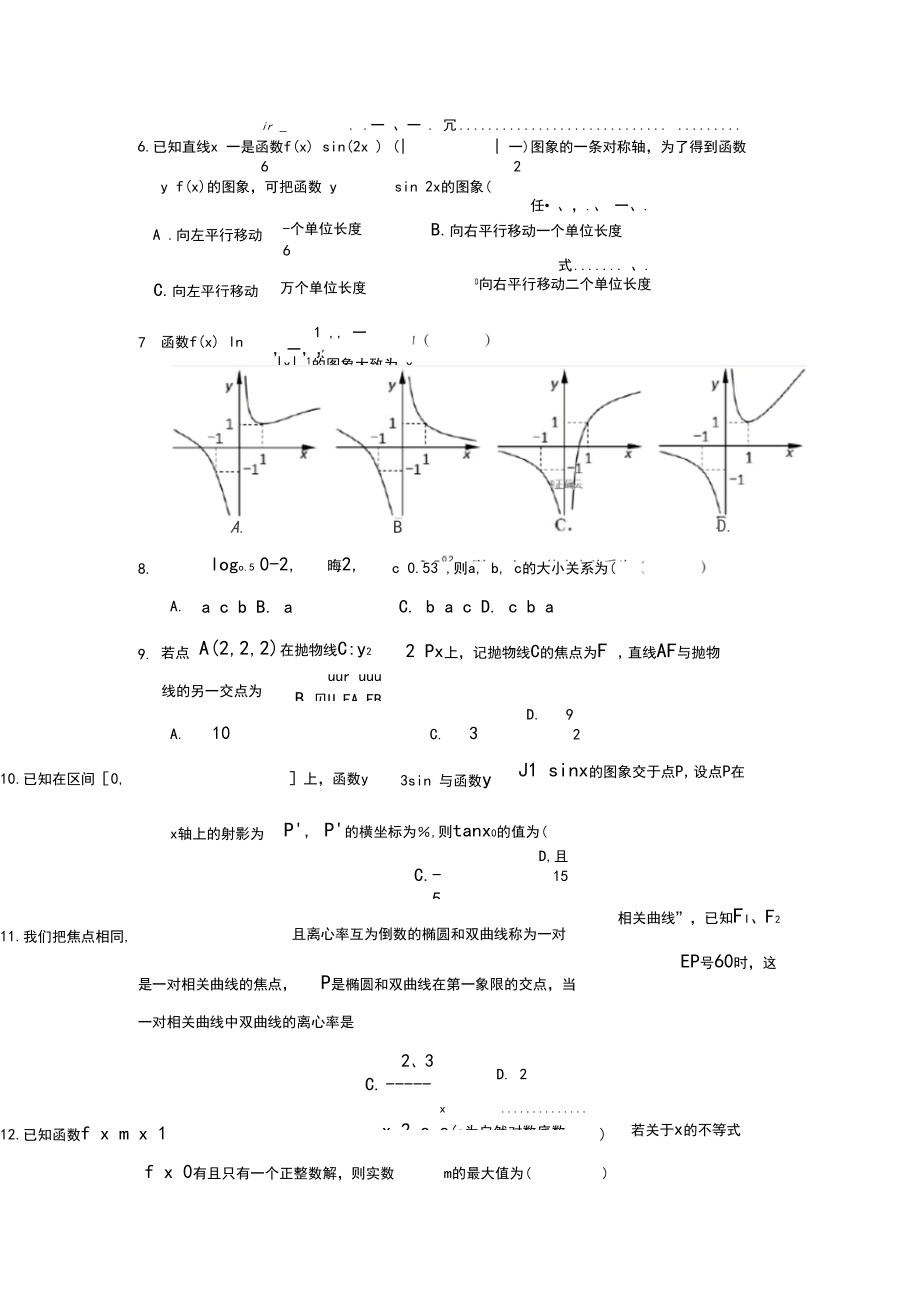
3、 .一 、一 . 冗 6.已知直线x 一是函数f(x) sin(2x ) (| 一)图象的一条对称轴，为了得到函数62y f(x)的图象，可把函数 ysin 2x的图象(A .向左平行移动-个单位长度6任 、，.、 一、.B.向右平行移动一个单位长度68.9.C.向左平行移动万个单位长度式、.D向右平行移动二个单位长度函数f(x) ln7.D.A.B .logo.5 0-2, b晦2,A.1 , 一 ，一，|x| 1的图象大致为 xc 0.53 ,则a, b, c的大小关系为(a c b B. aC. b a c D. c b a若点A(2,2,2)在抛物线C:y22 Px上，记抛物线C的焦点

4、为F ,直线AF与抛物线的另一交点为uur uuuB,贝U FA FBA.10C. 310.已知在区间0,上，函数y3sin 与函数yD. 92J1 sinx的图象交于点p,设点p在x轴上的射影为P', P'的横坐标为,则tanx0的值为(C.-5D,且1511.我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对相关曲线”，已知Fi、F2是一对相关曲线的焦点，P是椭圆和双曲线在第一象限的交点，当EP号60时，这一对相关曲线中双曲线的离心率是2、3C.3D. 212.已知函数f x m x 1xx 2 e e(e为自然对数底数),若关于x的不等式f x 0有且只有一个正整数解

5、，则实数m的最大值为()3e eB.A . 八2二、填空题:第n卷(非选择题本大题共 4小题，每小题5分.共90分)r ：一什13.已知a, b为互相垂直的单位向重，右rc贝 r b ra14 .已知函数f(x) x3 2x,若f(a 1) f(2a2) 0,则实数a的取值范围是.15 .数列an是等差数列，q 1,公差de 1, 2,且周 口0 % 15,则实数 的 最大值为.16 .已知矩形ABCD, AB 1, BC J3,将4ADC沿对角线AC进行翻折，得到三 棱锥D ABC ,则在翻折的过程中，有下列结论正确的有.三棱锥D ABC的体积的最大值为 1 ；3三棱锥D ABC的外接球体积

6、不变；三棱锥D ABC的体积最大值时，二面角 D AC B的大小是60 ;异面直线 AB与CD所成角的最大值为90 .三、解答题：共70分.解答应写出文字说明、 证明过程或演算步骤.第1721题为必考题， 每个试题考生都必须作答.第 22, 23题为选考题，考生根据要求作答 .(一)必考题：共 60分.17 .(本小题满分12分)在 ABC中，内角A,B,C的对边分别为a, b, C,已知b acosC -c . 2(i)求角A；(n)若AB?AC 3,求刷最小值.18 .(本小题满分12分)中华人民共和国个人所得税法规定，公民月收入总额(工资、薪金等)不超过免征额的部分不必纳税，超过免征额的

7、部分为全月应纳税所得额，个人所得税税款按税率表分段累计计算。为了给公民合理减负，稳步提升公民的收入水平，自2018年10月1日起，个人 所得税免征额和税率进行了调整，调整前后的个人所得税税率表如下:个人所得税税率表(调整前)个人所得税税率表(调整后)免征额3500元免征额5000元级数全月应纳税所得额税率级数全月应纳税所得额税率1不超过1500元的部分3%1不超过3000元的部分3%2超过1500元至4500元的部分10%2超过3000元至12000元的部分10%3超过4500元至9000元的部分20%3超过12000元至25000元的部分20%(I)已知小李2018年9月份上交的税费是 29

8、5元，10月份月工资、薪金等税前收入与9月份相同，请帮小李计算一下税率调整后小李10月份的税后实际收入是多少？(n)税务部门在小李所在公司用分层抽样方法抽取某月100位不同层次员工的税前收入，并制成下面的频率分布直方图。(i )请根据频率分布直方图估计该公司员工税前收入的中位数；(ii)同一组中的数据以这组数据所在区间中点的值作代表，按调整后税率表，试估计小李所在的公司员工该月平均纳税多少元？19 .(本小题满分12分)如图，在底面为矩形的四棱锥 P ABCD中，平面PAD平面ABCD.,4B(I)证明：AB PD； (n)若PA PD AB, APD 90，设Q为PB中点，求直线AQ与平面P

9、BC所成角的余弦值.20 .(本小题满分12分)已知椭圆E ：与 4 1ab 0的离心率为巫,以椭圆E的长轴和短轴为对 a2b22角线的四边形的面积为 472 .(I)求椭圆E的方程；(n)若直线x my 4 0与椭圆E相交于A , B两点，设P为椭圆E上一动点,uuuuucULMuuuuuir且满足PAPBt 2 OP(O为坐标原点).当t 1时，求OAOB的最小值.21 .(本小题满分12分)2已知函数f (x) a In x - xx 1e( a为常数)在区间(o, 2)内有两个极值点x%*2(4x2)(I)求实数刖取值范围;(n)求证：x x2 2(1 Ina).(二)选考题：共10分

10、.请考生在第22, 23题中任选一题作答.如果多做，那么按所做的 第一题计分.22 .(本小题满分10分)选彳% 44:坐标系与参数方程 xcos已知在平面直角坐标系 xOy中，圆C的参数万程为(为参数).以原y 1 sin点O为极点，冲由的非负半轴为极轴，取相同的单位长度建立极坐标系.(I)求圆C的普通方程及其极坐标方程；一与圆C的交点6(n)设直线I的极坐标方程为 sin 2 ,射线om3为P (异于极点)，与直线I的交点为Q ,求线段PQ的长.23 .(本小题满分10分)选彳45:不等式选讲已知函数 f(x) |x 21 a|x 2|,(I )当a=2时，求不等式f (x) 2的解集；(

11、n)当x 2,2时不等式f(x) x恒成立，求a的取值范围、选择题数 学（理科）参考答案题号123456789101112答案CBBADCAADBAC二、填空题：2ii13.-14. 1,15.16.222三、解答题：117.斛：（I） '.-A ABC 中，b acosC c, 21 . .由正弦te理知， sin B sin AcosC sinC , 2 分2-1 sin B sin( A C) sin Acos C sin C cos A ,sin C cos A sin AcosC sinC, 4分2ABCsin AcosCsin C cos AA 一. 6分3A 1一cos

12、A 一 , 2（n） . AB?AC 3. AB?|AC|cosA 3,得 bc 68分所以 a2 b2 c2 2bc cos A b2 c2 6 2bc 6 6当且仅当b c时取等号 11分所以a的最小彳1为 J6 12分18.解：（I）设小李9月份的税前收入为 X元，因为295 345所以按调整起征点前应缴纳个税为：1500 3% x 5000 10% 295,解得x 7500 2分按调整起征点后应缴纳个税为：7500 5000 3% 75调整后小李的实际收入是 7500 75 7425 （元）4分（n） （i）由柱状图知，中位数落在第二组，不妨设中位数为X千元，则有 0.12 2 0.1

13、6 x 5 0.5,解得 x 6.625 （千元）估计该公司员工收入的中位数为6625千元.（ii）按调整起征点后该公司员工当月所交的平均个税为0.24 0 0.32 30 0.2 90 0.12 290 0.08 490 0.04 690 129.2 （元）估计小李所在的公司员工平均纳税129.2元12分19.解：（I）依题意，平面 PAD平面ABCD, AB AD1分QAB 平面ABCD ,平面PAD I平面ABCD AD , 2分AB平面PAD,又PD 平面PAD4分AB PD5 分(n)在 4PAD中，取 AD 中点 O ,连接 PO , Q PA AD, PO AD, PO 平面AB

14、CD,以O为坐标原点，分别以OA为我由，过点A且平行于AB的直线为y轴，OP所在的直线为轴，建立如图所示空间直角坐标系. 6 分设 PA 2, Q APD 90 , AD 2".P(0,0, J2), B( J2,2,0),C( 2,2,0), A( .2,0,0), Quuu _ uuirPB ( ,2, 2, 12), BC一uuir(2,2,0,0), AQ设平面pbc的法向量为n(x,y, z),r n 则rnuuu-PB2x 2y 2z 0uur -BC 2、2x 01,得 n（0,1物设直线AQ与平面PBC所成角为，则sin uuir r cos . AQ, nuuir

15、rAQ nuutrAQ n10分因为所以直线AQ与平面PBC所成角的余弦值为312分20.解:c .2(i)依题意得， e J.以椭圆E的长轴和短轴为对角线的四边形的面积 a 21则2a 2b 4,2, 2所以椭圆22E的方程为421.(n)设A,B两点的坐标分别为(Xi, y), (x2, y2),联立方程uuu 因为PA所以点p(2my8m2 muur PB1,得(m2 2)y2 8my 12 0,64 m2 9604,2，y22uuu1223m2 2uuu uuut 2 OP,即 OA OPuur uurOB OP tuur uuu uuu2 OP ,所以 OA OBuuutOP .X1

16、X2y1上)，又点P在椭圆C上，所以有X2 )22( y1y2)2化简得n% y2)822(yiy2)24t2,所以8m2 /2)(m22)16m(8m2)64 4t2 0 ，化简 m232t2因为t 1,所以26 m2因为uuu uuuOA OBX1X2yemy1 4my21 丫也 4m y1y216 ，Y28mm2 2，Y1Y212m2 2uu uuuOA OB4 m2 442m2 2uuu uuu2 s(s (8,32),则 oa ob4s 525211分” , uuu uuu1932时，OA OB取得最小值，最小值为-921 .解：(I )解法41分2ex1 一、 (2 x)(e 1

17、ax)由 f(x) a Inx -,可得 f (x) 3 1分x xx由题意 x (0,2),则，x 0,设 h(x) e"1 ax(x 0),h(x) ex 1 a . x由题意，知 x1, x2是y h(x)在(0, 2)上的两个零点.当a< 0时，h (x) 0 ,则h(x)在(0, 2)上递增，h(x)至多有一个零点，不合题意； 2分当 a 0时，由 h (x) 0 ,得 x 1 ln a , h(1 In a) a In a3 分(i)若 1 Ina 2 且 h(2) e 2a 0,即 0 a £ 时，h(x)在(0,1 In a)上递减，2(1 In a,

18、2)递增；若h(x)minh(1 Ina) alna40,即0 a w e时，h(x)至多有一个零点，不合题意,舍去;若 h(x)min h(1 Ina) alna 0,即 1 a £时，又 Qh(2) 0,h(0) 1 0, 2e从而，h(x)在(0,1 In a)和(1 In a, 2)上各有一个零点.所以1 a e时，y h(x)在(0, 2)上存在两个零点. 4分(ii)若1 In a 2 ,即a e时，h(x)在(0, 2)上单调递减，h(x)至多有一个零点，舍去5分e(iii)若 1 Ina 2 且 h(2) e 2a < 0 ,即一< a e 时，h(x)在

19、(0,1 In a)上有一个 2零点，在(1 In a,2)上没有零点，舍去.综上可得，实数a的取值范围是解法二：由 f (x) a In xx 1 e F ,可得f (x)x(2 x)(ex1 ax)由题意x (0,2),则Ix 10,由题意知x1,x2是y eax, x 0在(0, 2)上的两个零点.x 1由 y e ax 0,得 a从而只需直线 y a与函数g（x）的图象在（0, 2）有两个交点.分由 g(x) (x 2)e 得 g(x)xe所以H (x)在(0,1 In a)上递增，8分H(x1) h(x1) h(2 2lna x) H(1 Ina) 0 1价而 h(x) h(&

20、;)， 且 h(x)在(1 In a, 2)递增;h(%) h(2 2lna ») 分1解法二：由(1)有ax2ex 1X2 1 eln aln x1x11ln aln x2x212ln a ln(x1x2) x1 x2 2则证明 x1x22(1 lna)ln(xx2) 00 x1x2 11x2 x1x 1!一在区间（0,1）内单调递减，在区间（1,2）内单调递增,xe 所以 g(x)min g(1) 1, g(2)二. 4分2且 x 0 时，g(x) . 5分所以实数a的取值范围是 1,e . 6分2(n)解法一：令 H (x) h(x) h(2 2ln a x), 0 x 1 In a7分x 1a2则 H(x) h(x) h(2 2lna x) e 卞 2a)2a 2a 0,x2 2 2lna x1, x1 x2 2(1 lna),命题得证.12分下证式成立，由ex1 ax 0,得a exex 1ex 1 (x 1)令 g(x) 一，则 g(x) gd), g(x) 2-9xx易知0 x 1”,从而式X2g(x2)10分又令 G(