201x秋八年级数学上册 12.1 全等三角形1 新人教版

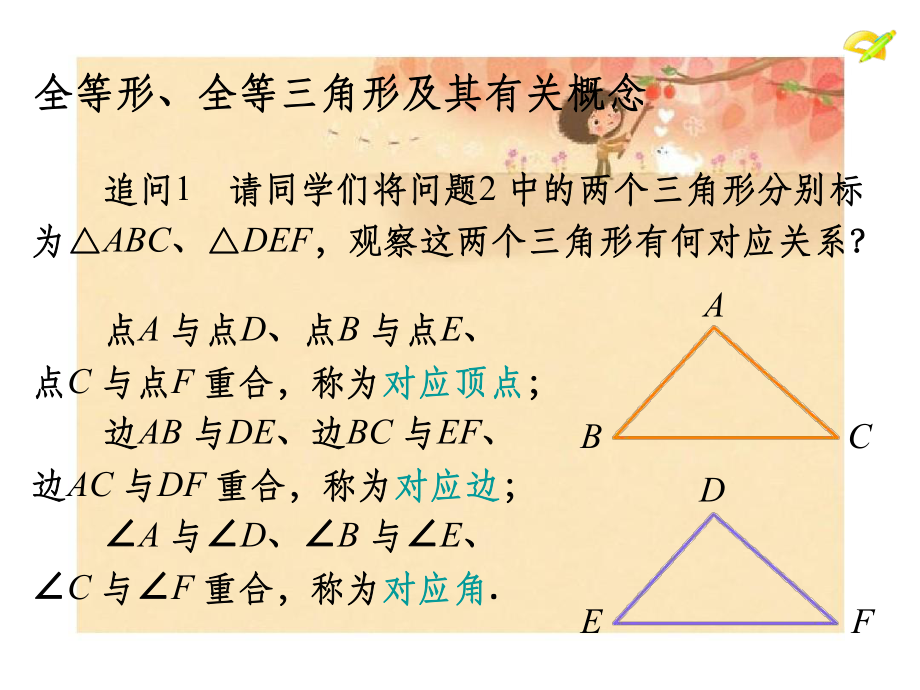
1、12.1 全等三角形全等三角形问题问题1观察这些图片，你能看出形状、大小完全观察这些图片，你能看出形状、大小完全一样的几何图形吗？一样的几何图形吗？生活中的全等形生活中的全等形 追问你能再举出生活中的一些类似例子吗？追问你能再举出生活中的一些类似例子吗？生活中的全等形生活中的全等形 问题问题2 请同学们用复写纸画出两个三角形，并请同学们用复写纸画出两个三角形，并用剪刀剪下其中一个三角形，观察这两个三角形有何用剪刀剪下其中一个三角形，观察这两个三角形有何关系？关系？全等形的定义：全等形的定义：能够完全重合的两个图形叫做全等形能够完全重合的两个图形叫做全等形全等三角形的定义：全等三角形的定义：能够

2、完全重合的两个三角形叫做全等三角形能够完全重合的两个三角形叫做全等三角形全等形、全等三角形及其有关概念全等形、全等三角形及其有关概念问题问题3 请同学用语言归纳出问题请同学用语言归纳出问题1 和问题和问题2 中两个中两个 图形有何关系？图形有何关系？点点A 与点与点D、点、点B 与点与点E、点点C 与点与点F 重合，称为重合，称为对应顶点对应顶点； 边边AB 与与DE、边、边BC 与与EF、边边AC 与与DF 重合，称为重合，称为对应边对应边； A 与与D、B 与与E、C 与与F 重合，称为重合，称为对应角对应角. 全等形、全等三角形及其有关概念全等形、全等三角形及其有关概念追问追问1请同学们

3、将问题请同学们将问题2 中的两个三角形分别标中的两个三角形分别标为为ABC、DEF，观察这两个三角形有何对应关系？，观察这两个三角形有何对应关系？ AB C D E FABC与与DEF是全等的，是全等的，记作：记作：“ABC DEF”， 读作：读作：“ABC 全等于全等于DEF” 全等形、全等三角形及其有关概念全等形、全等三角形及其有关概念追问追问2你能用符号表示出这两个全等三角形吗？你能用符号表示出这两个全等三角形吗？AB C D E F图（图（1）中，）中，ABC DEF；图（图（2）中，）中，ABC DBC；图（图（3）中，）中，ABC AED. . 全等形、全等三角形及其有关概念全等形

4、、全等三角形及其有关概念问题问题4请同学们拿出问题请同学们拿出问题2 准备的素材，按照教准备的素材，按照教材第材第32 页图页图- -2 进行平移、翻折、旋转，变换前后进行平移、翻折、旋转，变换前后的两个三角形还全等吗？的两个三角形还全等吗？ 追问你能说出它们的对应顶点、对应边和对应追问你能说出它们的对应顶点、对应边和对应 角吗？角吗？全等三角形的性质：全等三角形的性质： 全等三角形的对应边相等、全等三角形的对应边相等、对应角相等对应角相等. .全等三角形的性质全等三角形的性质问题问题5全等三角形的对应边和对应角有何大小关全等三角形的对应边和对应角有何大小关 系？系？AB C D E F用几何

5、语言表述：用几何语言表述：ABC DEF， AB = =DE，BC = =EF，AC = =DF （全等三角形的对应边相等），（全等三角形的对应边相等），A =D，B =E，C =F （全等三角形的对应角相等）（全等三角形的对应角相等）全等三角形的性质全等三角形的性质问题问题5全等三角形的对应边和对应角有何大小关全等三角形的对应边和对应角有何大小关系？系？AB C D E FD课堂练习课堂练习练习练习1如图，如图，OCA OBD，点，点C 和点和点B，点，点A与点与点D是对应点，则下列结论错误的是（是对应点，则下列结论错误的是（ ） （A） COA =BOD ； （B） A =D ； （C）

6、CA = =BD ； （D） OB = =OA CBOAD练习练习2ABN ACM， ABN 和和ACM 是对是对 应角，应角，AB 和和AC 是对应边则下列结论错误的是是对应边则下列结论错误的是（ ） （A）AMC = =ANB ； （B）BAN = =CAM ； （C）BM = =MN ； （D）AM = =AN 课堂练习课堂练习ABCMN练习练习3如图，如图，ABC CDA，AB 与与CD，BC 与与 DA 是对应边，则下列结论错误的是（是对应边，则下列结论错误的是（ ） （A） BAC = DCA ； （B）AB /DC ； （C） BCA = DCA ； （D）BC /DA ABCD课堂练习课堂练习练习练习4如图，如图，EFG NMH，F 和和M 是对是对 应角应角（1）FG 与与MH 平行吗？为什么？平行吗？为什么？（2）判断线段）判断线段EH 与与NG 的大小关系，并说明理由的大小关系，并说明理由（1）平行；）平行；（2）相等）相等HENGFM课堂练习课堂练习（1）本节课学习了哪些内容？）本节课学习了哪些内容？（2）结合本节课的学习，谈谈如何寻找全等三角形的）结合本节课的学习，谈谈如何寻找全