地图系统及基本的土地测量知识

1、4.0 地图系统和土地测量的基础知识内容4.1地球模型4.2坐标系统4.2.1 笛卡尔坐标4.3局部坐标系统4.3.1 澳大利亚UTM数据及地图坐标4.3.2UTM坐标系统4.4北点和北向4.4.1真北或地理北4.4.2磁北4.4.3坐标北4.4.4象限4.4.5方位角4.4.6东偏北或西偏北4.5坐标角度和磁角度、磁角度和坐标方位角的换算4.5.1磁北换算为坐标北4.5.2坐标北换算为磁北4.6根据方位角和距离计算参考坐标4.7换算公式：十进制度数换算成度数，分和秒换算成度数，分和秒换算成十进制度数 4.7.1将十进制度数换算成度、分、秒4.7.2将度、分、秒换算成十进制度数4.8全球定位系

2、统（GPS）4.8.1GPS 简介4.8.2GPS发展简史4.8.3GPS的基本概念4.8.4GPS在工矿企业中的应用4.8.5GPS的发展前景4.1 地球模型 在过去的很多年中，很多人都试图对地球表面做出精确的描述，困难之处在于：地球并非一个完美的球体，而人类却希望每样东西都是方方正正的。 人们用数学上的椭圆体来定义地球、大地水准面，这样就便于进行测量计算、建立坐标和高程模型。 一般来说，测地基准点或参考大地水准面都是以局部为中心的，并非以地球为中心。随着GPS的出现，人们制造出了一个地心模型，即WGS84。以另一椭圆体为参照物，地球这个椭圆体和参照的椭圆体有明显差异，这种差异可以是几毫米，

3、也可以是数百米，作为一名舵手，这时你就该意识到你正在操纵的椭圆体模型应和其参照点保持一致。 下表列出了过去150年中对地球这个椭圆体进行的定义，注意：还有很多并未列出。名称赤道轴 (m)极轴 (m)Clarke 18666 378 206.46 356 583.8Bessel 18416 377 397.1556 356 078.965International 19246 378 3886 356 911.9Krasovsky 19406 378 2456 356 863GRS 19806 378 1376 356 752.3141WGS 19846 378 1376 356 752.314

4、2Sphere (6371 km)6 371 0006 371 0004.2 坐标系统 为简化笛卡尔坐标系统（经纬度）的翻译过程，我们一般采用直角坐标系统。 这些坐标可能和经度线和纬度线不一致。世界气象组织方块、c方块和马士顿方块是一致的，而墨卡托方位法（UTM）和其他局部坐标系统则不一致。 不一致的情况主要有两种：等角或等面积。 等角坐标指在同一区域的某些不同部分经度和纬度的角度一样。 等面积坐标指在整个区域内距离相等，但不能用经度数表示。 最有影响力的三角坐标就是Geoffrey Dutton 20世纪80年代提出的“四元三角网（QTM）”了，人们对这种观点进行系统总结，并于1999年出版

5、。1.02.03.04.04.14.24.2.1 笛卡尔坐标 笛卡尔坐标（也称为直角坐标系），在这个平面坐标体系中，每个点都可以用一对坐标来表示。对于平面内任意一点C，过点C分别向X轴、Y轴作垂线，垂足在X轴、Y轴上的对应点a,b分别叫做点C的横坐标、纵坐标，有序实数对（a,b）叫做点C的坐标。 坐标系中的两条参考线就称为x轴和y轴，两坐标轴的公共原点叫做直角坐标系的原点。 我们也可以用笛卡尔坐标定义三维空间中的任意一个点及计算这个点到三个互相垂直的平面之间的距离。推而广之，笛卡尔坐标可以在任意空间中定义任何一个点及计算这个点到互相垂直超平面的距离。 17世纪法国伟大的数学家和物理学家笛卡尔，

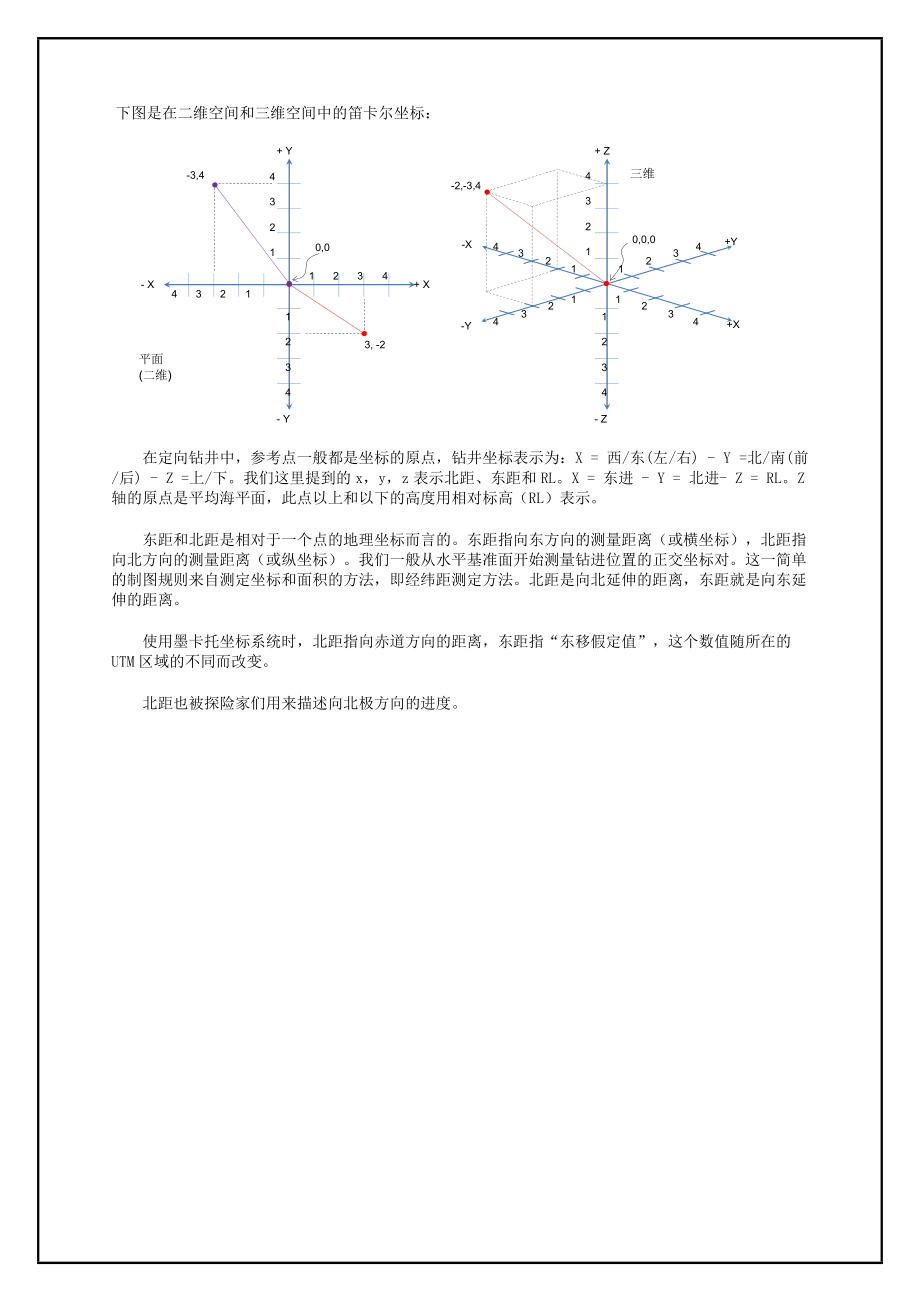
6、他将欧几里德几何和代数有机联系起来，创立了笛卡尔坐标。在笛卡尔坐标系统中，几何形状（如曲线）也可以用笛卡尔方程表示，即关于几何形状上某个点的代数方程。 笛卡尔坐标系是解析几何学的基础，也为很多数学分支如线形代数、复变函数、微分几何、微积分学、群论等提供了几何解释。函数图像就是我们熟悉的例子。笛卡尔坐标在几何学包括天文学、物理学、工程等方面发挥重要作用。笛卡尔坐标也普遍应用在计算机绘图、计算机辅助规划设计及其他几何相关的数据处理中。 在解析几何中，一个平面上的未知坐标或通用坐标经常用字母x和y表示，在三维空间中也用到字母z（字母w经常用在四维空间中，只是很少用到）。 下图是在二维空间和三维空间中

7、的笛卡尔坐标： 平面(二维)三维 在定向钻井中，参考点一般都是坐标的原点，钻井坐标表示为：X = 西/东(左/右) - Y =北/南(前/后) - Z =上/下。我们这里提到的x，y，z表示北距、东距和RL。X = 东进 - Y = 北进- Z = RL。Z轴的原点是平均海平面，此点以上和以下的高度用相对标高（RL）表示。 东距和北距是相对于一个点的地理坐标而言的。东距指向东方向的测量距离（或横坐标），北距指向北方向的测量距离（或纵坐标）。我们一般从水平基准面开始测量钻进位置的正交坐标对。这一简单的制图规则来自测定坐标和面积的方法，即经纬距测定方法。北距是向北延伸的距离，东距就是向东延伸的距离

8、。 使用墨卡托坐标系统时，北距指向赤道方向的距离，东距指“东移假定值”，这个数值随所在的UTM区域的不同而改变。 北距也被探险家们用来描述向北极方向的进度。4.3 局部坐标系统 我们常见的国家坐标系统也是局部坐标系统的一种形式。 澳大利亚有很多的坐标系统，第一个就是二战期间形成的，即我们今天称为的“澳大利亚国家坐标（ANG）系统”。 根据横轴麦卡托投影，ANG可用于制作地形图和地质图。 以经度50为基础，在中央子午线的任一侧延伸+/- 2.50。 当澳大利亚的公制长度变为米时，坐标系统就改为米制坐标系统，此系统也采用了墨卡托方位法。 在100,000m的坐标方格下，塔斯马尼亚的中央子午线向东移

9、了1470。 由此我们可以看到，这两种局部坐标系统有明显区别。 一些采矿企业也会根据自身需求研发特定的矿井坐标。4.3.1 澳大利亚的UTM基准线及地图坐标 澳大利亚目前的UTM坐标系统的经纬度采用GDA94基准线（1994年澳大利亚地心基准线）和MGA94地图坐标（1994年澳大利亚地图坐标）取代AGD66基准线（1966年澳大利亚地心基准线）和AMG66地图坐标（1966年澳大利亚地图坐标）；在澳大利亚某些地方，也采用AGD84和AMG84作为坐标系统。地图坐标的变化导致了UTM坐标的变动，所以在每次记录或出版UTM坐标系统时，要标出采用的基准线。 GDA94和WGS84的使用范围差不多，

10、两者也就相差几公分。 对澳大利亚的GPS使用者来说，需要根据最新的地图坐标调整、更新他们的GPS接收器。4.34.3.14.3.2 UTM坐标系统 UTM系统是在全世界范围内通用的米制坐标系统。在UTM系统中，按照经度每6度为一个区，世界被分成60个区。 在UTM系统中，对南半球的划区采用北移假定值，这样就可以确保所有的北距都为正值。Figure 4-1 下面两幅图分别是世界UTM区划图（图4-1）和澳大利亚UTM区划图（图4-2）。Figure 4-1图 4-24.4 北点和北向 下面三个图表列出了在井眼测量中测量方向的主要参考点：4.4.1 地理北 真北或地理北-又称正北方向，为过地球上一

11、点指向地球地理北极的方向。4.4.2 磁北（见图4-3） 磁北方向既磁子午线北向，为过地球上一点指向地球磁北极的方向，亦既磁针静止时，磁北针所指方向。图 4-3 磁北4.4.3 坐标北（见图4-4） 为给人们观察世界提供一个更为可行的方法，我们假定地图上构成坐标系统的经线都是平行的，虽然在现实世界里，这些经线在南极和北极会交汇于一点。图 4-4 交汇 在这样的坐标系统中，坐标北在某个点会和沿经纬线的真北重合，这就为坐标提供了参照点。在坐标系统的其他点上，坐标北都会偏离真北。 偏离的角度称为收敛角，收敛角的度数在坐标系统内也时时变化。如若需要，可采用校正倾斜角的方法校正收敛角的度数。 一般采用如

12、下三种方法测量和描述方向：4.4.4 象限（见图4-5）图4- 5 象限 坐标系里的横轴和纵轴所划分的四个区域，分为四个象限。象限以原点为中心，x，y轴为分界线。右上的称为第一象限，左上的称为第二象限，左下的称为第三象限，右下的称为第四象限。原点不属于任何象限。象限法的好处是直观、清晰，缺点是在从一个象限转换到另一个象限时，进行倾斜角校正和调查计算时容易出错。4.4.5 方位角（见图4-6） 方位角是在平面上量度物体之间的角度差的方法之一。是从某点的指北方向线起，依顺时针方向到目标方向线之间的水平夹角。 方位角法大大降低了出现上述错误的可能性，也简化了调查计算过程。图 4- 6 方位角4.46

13、 东偏北或西偏北（见图4-7） 在这种方法中，东偏北是正向，西偏北为负向。以北向为参考点：以东为正向，以北为负向图中方向A可以表示为6°W or -6°方向B可以表示为8°E or -8°图 4- 7东偏北或西偏北4.44.5 坐标角度和磁角度、磁角度和坐标方位角的换算 要了解坐标角度和磁方位角，就要先了解地图的布局和符号。 一幅地图中显示有地图数据、图例、指向标、东距线和北距线。 北距线是在地图上画出的一条线，和赤道的南北向平行，这条线贯穿整个地图。 东距线是在地图上画出的一条线，从北极到南极，即从地图的顶部到底部。 真北 -指向北极的真方向（见图4-

14、8） 坐标北 - 地图上显示的北方 Figure 4-8磁北 - 指向标上显示的北方4.5.1 磁北换算为坐标北 将罗盘方位角换算成坐标方位角时，需要加上根据地图指向标计算得出的磁偏角的角度。4.5.2 坐标北换算为磁北 将坐标方位角换算成罗盘方位角时，需要减去根据地图指向标计算得出的磁偏角的角度。坐标的方向 中心为原点 (见图 4-9)若选定位置在原点以北，就为正向。若选定位置在原点以南，就为负向。图4-9 从平面直角坐标换算成极坐标时，就必须从第一套平面直角坐标的角度中减去第二套平面直角坐标的角度。下面是两套平面直角坐标体系，标记为Peg 1和Peg 2。 下图中的原点为Peg 1。 从P

15、eg 2 中的北向坐标度数中减去Peg 1 中的北向坐标度数，从Peg 2 中的东向坐标度数中减去Peg 1 中的东向坐标度数。Peg 2Peg 1 -北 7569722.750东604932.940Peg 2 -北7569744.300东604954.560Peg 1 差异 北 + 21.550 东 + 21.620这两套坐标系统之间的差异说明Peg 2 在Peg 1的东北方向。（见图4-10） 4.6 根据方位角和距离计算参考坐标 要根据方位角和距离计算参考坐标，首先要采用简单的三角函数确定极坐标，然后从水平井井口处加上或减去极坐标，得出水平井井口的参考坐标，然后再计算得出直井井口的参考坐

16、标。右图中水平井井口坐标的原点为 Peg 1。Figure 4-22 注意：若你要求的坐标（示例图中为直井井口坐标 Peg 2）在原点以北，你得到的坐标值为正数。 若你要求的坐标在原点以南，你得到的坐标值为负数。 下图中（见图4-22），水平井的井口坐标为Peg 1， 直井的井口坐标为Peg 2。由图中我们可知，直井的井口坐标在水平井的井口坐标的东北方向，方位角为45°。 Peg 1 平面到Peg 2 平面的距离为2474.87m。在这个直角三角形中，sin A = a/c; cos A = b/c; tan A = a/b. 这些都是一个直角三角形的基本要素（见图4-23）为方便记

17、忆，可表示为SOH-CAH-TOA，即：Sine = Opposite / HypotenuseCosine = Adjacent / HypotenuseTangent = Opposite / Adjacent图 4-23 对边 a 斜边 2474.87m列出等式： sin 45° = = a = 2474.87 x sin 45°Sin45º  = 0.707  (可用正弦表或计算器算出。) 所以.a = 2474.87 x 0.707因此，答案为 a = 1750m因为这是一个直角三角形，一个锐角为45°，并且我们已经知道了对

18、边的长度，因为是等腰直角三角形，邻边和对边长度一样。若直角三角形中其他两个角的度数不一样，我们可以采用如下方法计算邻边的长度。 邻边 b 斜边 2474.87m列出等式: cos 45° = = b = 2474.87 x cos 45°Cos45º  = 0.707 (可用余弦表或计算器算出。) 所以.b = 2474.87 x 0.707因此，答案为.b = 1750m为Peg 1 北距加上北极坐标， Peg 1 的东距加上动东极坐标。 Peg 1 -北距 7 200 000.00 东距 650 000.00 差异 -北距+ 1750.00

19、 东距 + 1750.00 Peg 2 -北距 7 201 750.00东距 651 750.004.7 换算公式：十进制度数换算成度数，分和秒换算成度数，分和秒换算成十进制度数我们经常需要在十进制度数、度数、分秒之间进行换算。许多计算软件都有这一功能。即使如此，我们也需要知道如何进行换算。 简单来说，应掌握如下内容：一个圆可分为360度，每度可分为60分，每分可分为60秒。 例如：GPS坐标经常用经纬度格式表示，而经纬度可根据精确度的要求有多种表示方法。d=度 m=分 s=秒dd.ddd- Decimal Degrees (i.e. 12.345°)dd mm.m- Degrees

20、 & Minutes (i.e. 12° 20.7')dd mm ss- Degrees, Minutes & Seconds(i.e. 12° 20'42")这个公式非常简单，很容易掌握。4.7.1 将十进制度数换算成度、分、秒度数保持不变 (i.e. in 121.135° longitude, start with 121°). 将小数点后面的度数乘以 60 (i.e. .135 * 60 = 8.1). 就变成了用分表示的度数 (8'). 再将小数点后面的数字乘以 60. (i.e. .1 * 6

21、0 = 6). 就变成了用秒表示的度数(6"). 用秒表示时可能还有小数点。然后将用度(°)、分(')、秒(")表示的度数放在一起。 (i.e. 121°8'6" longitude)4.7.2 将度、分、秒换算成十进制度数将度、分、秒换算成十进制度数时可使用下列公式：度 + (分/60) + (秒/3600)例如将42deg, 08min, 10sec 换算成十进制度数： 42 + (8/60) + (10/3600) = 42.1361°4.8 全球定位系统(GPS)4.8.1 GPS简介 全球定位系统(GPS)是

22、美国国防部研发的一种全球导航卫星系统。GPS定位的基本原理是 GPS定位原理：根据高速运动的卫星瞬间位置作为已知的起算数据，采用空间距离后方交会的方法，确定待测点的位置。 GPS可以为世界的万物如山脉、河流、森林、濒危动物、珍贵矿藏等提供准确的三维定位信息，可显示在地图或模型上。这些信息可作为GIS系统的原始输入信息，对这些信息进行汇编、存储、操作等，就成了地理学上的参考信息。4.8.2 GPS发展简史 美国海军最初使用的卫星导航系统Transit是1960年研制的。采用五颗试验卫星，可以每小时确定航向。1967年，美国海军又研制了Timation， 可将精确时钟用在宇宙空间中，为研发GPS技

23、术奠定了基础。 20世纪70年代，建立在信号相位比较基础上的路基欧米加导航系统，成为第一个世界上通用的无线电导航系统。 GPS的设计部分基于路基无线电导航系统，如二战时使用的LORAN和Decca 导航器。 1957年前苏联发射第一颗人造卫星加速了美国研发GPS的步伐。美国组成了一个专家组检测此卫星的无线电传输信号。这些专家发现，人造卫星越接近其他卫星，它发射的信号频率就越高，反之亦然。他们意识到，因为他们知道他们在地球上的确切位置，就可以通过测量多普勒的失真情况来确定卫星沿着既定轨道运行到了何处。4.8.3 GPS的基本概念 GPS由三部分构成：绕地球运行的卫星、控制检测站、用户使用的GPS接收器。GPS接收器可以获取并鉴定从太空传来的GPS卫星广播信号，由此可以给出三维位置（经度，纬度和海拔）外加时间。 GPS接收器通过对地球上空的GPS卫星发送的信号测定时间来确定位置。每个卫星都在连续不断地传送信息，包括信息传送的时间、准确地轨道信息、通用系统状态及所有GPS卫星的大致轨道。接收器测量每条信息的传送时间并计算到每个卫星的距离。这里要用到几何三边测量法将这些距离和卫星的位置结合起