



下载本文档
版权说明:本文档由用户提供并上传,收益归属内容提供方,若内容存在侵权,请进行举报或认领
文档简介
PAGEPAGE1课时作业11直线与平面平行的判定——基础巩固类——1.b是平面α外的一条直线,下列条件中可得出b∥α的是(D)A.b与α内的一条直线不相交B.b与α内的两条直线不相交C.b与α内的多数条直线不相交D.b与α内的全部直线不相交解析:b是平面α外的一条直线,要使b∥α,则b与平面α无公共点,即b与α内的全部直线不相交.2.下列命题(其中a、b表示直线,α表示平面)中,正确的个数是(A)①若a∥b,b∥α,则a∥α;②若a∥b,a⊄α,则a∥α;③若a∥α,b⊂α,则a∥b.A.0个 B.1个C.2个 D.3个解析:①中a可能在α内;②中无b⊂α的条件,推不出a∥α;③中a与b还可能异面.故选A.3.若M、N分别是△ABC边AB、AC的中点,MN与过直线BC的平面β的位置关系是(C)A.MN∥βB.MN与β相交或MN⊂βC.MN∥β或MN⊂βD.MN∥β或MN与β相交或MN⊂β解析:MN是△ABC的中位线,所以MN∥BC,因为平面β过直线BC,若平面β过直线MN,则MN⊂β.若平面β不过直线MN,由线面平行的判定定理可知MN∥β,故选C.4.假如直线l、m与平面α、β、γ满意:β∩γ=l,m∥l,m⊂α,则必有(D)A.l∥α B.l⊂αC.m∥β且m∥γ D.m∥β或m∥γ解析:若α∩β=m,则m⊄γ,此时m∥γ,反之则m∥β;若α∩γ=m,则m⊄β,此时m∥β,反之则m∥γ.故选D.5.如图P为平行四边形ABCD所在平面外一点,Q为PA的中点,O为AC与BD的交点,下面说法错误的是(C)A.OQ∥平面PCD B.PC∥平面BDQC.AQ∥平面PCD D.CD∥平面PAB解析:因为O为▱ABCD对角线的交点,所以AO=OC,又Q为PA的中点,所以QO∥PC.由线面平行的判定定理,可知A、B正确,又四边形ABCD为平行四边形,所以AB∥CD,故CD∥平面PAB,故D正确,选C.6.点E,F,G,H分别是四面体ABCD的棱AB,BC,CD,DA的中点,则空间四面体的六条棱中与平面EFGH平行的条数是(C)A.0 B.1C.2 D.3解析:如图所示,由线面平行的判定定理可知BD∥平面EFGH,AC∥平面EFGH.7.如图,一块矩形木板ABCD的一边AB在平面α内,把这块矩形木板绕AB转动,在转动的过程中,AB的对边CD与平面α的位置关系是CD∥α或CD⊂α,缘由是CD∥AB.解析:无论如何,都有CD∥AB.8.如下图(1)所示,已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图(2)所示,则BF与平面ADE的位置关系是平行.解析:由图(1)可知BF∥ED,由图(2)可知,BF⊄平面AED,ED⊂平面AED,故BF∥平面AED.9.过三棱柱ABCA1B1C1的随意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有6条.解析:过三棱柱ABCA1B1C1的随意两条棱的中点作直线,记AC,BC,A1C1,B1C1的中点分别为E,F,E1,F1,则直线EF,E1F1,EE1,FF1,E1F,EF1均与平面ABB1A1平行,故符合题意的直线共6条.10.已知:△ABC中,∠ACB=90°,D、E分别为AC、AB的中点,沿DE将△ADE折起,使A到A′的位置,M是A′B的中点,求证:ME∥平面A′CD.证明:如图所示,取A′C的中点G,连接MG、GD.∵M、G分别是A′B、A′C的中点,∴MG綊eq\f(1,2)BC,同理DE綊eq\f(1,2)BC,∴MG綊DE,即四边形DEMG是平行四边形,∴ME∥DG.又∵ME⊄平面A′CD,DG⊂平面A′CD,∴ME∥平面A′CD.11.如图,三棱柱ABCA1B1C1中,D,E,F分别为棱AB,BC,A1C1的中点.证明:EF∥平面A1CD.证明:在三棱柱ABCA1B1C1中,AC∥A1C1,且AC=A1C1,连接ED,在△ABC中,因为D,E分别为AB,BC的中点,所以DE=eq\f(1,2)AC且DE∥AC,又F为A1C1的中点,可得A1F=DE,且A1F∥DE,即四边形A1DEF为平行四边形,所以EF∥DA1,又EF⊄平面A1CD,DA1⊂平面A1CD,所以EF∥平面A1CD.——实力提升类——12.下列四个正方体中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是(B)A.①③B.①④C.②③ D.②④解析:对图①,可通过证明PN中点与M的连线平行于AB得到AB∥平面MNP,对图④,可通过证明AB∥PN得到AB∥平面MNP,故选B.13.如图所示,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点,给出五个结论:①OM∥PD;②OM∥平面PCD;③OM∥平面PDA;④OM∥平面PBA;⑤OM∥平面PBC.其中正确的个数有(C)A.1 B.2C.3 D.4解析:矩形ABCD的对角线AC与BD交于O点,所以O为BD的中点.在△PBD中,M是PB的中点,所以OM是中位线,OM∥PD,则OM∥平面PCD,且OM∥平面PDA.因为M∈PB,所以OM与平面PBA、平面PBC均相交.14.如图所示,P是平行四边形ABCD所在平面外一点,E为PB的中点,O为AC,BD的交点,则与EO平行的平面有平面PAD、平面PCD.解析:在△DPB中,∵O为BD的中点,E为PB的中点,∴EO∥PD,又EO在平面PAD、平面PCD外,PD在平面PAD、平面PCD内,所以EO与平面PAD、平面PCD平行.15.如图,在正方体ABCDA1B1C1D1中,E是棱DD1的中点,在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.解:存在.证明如下:如图,取C1D1的中点F,连接B1A交A1B于点M,连接ME,EF,B1F,C1D.因为
温馨提示
- 1. 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
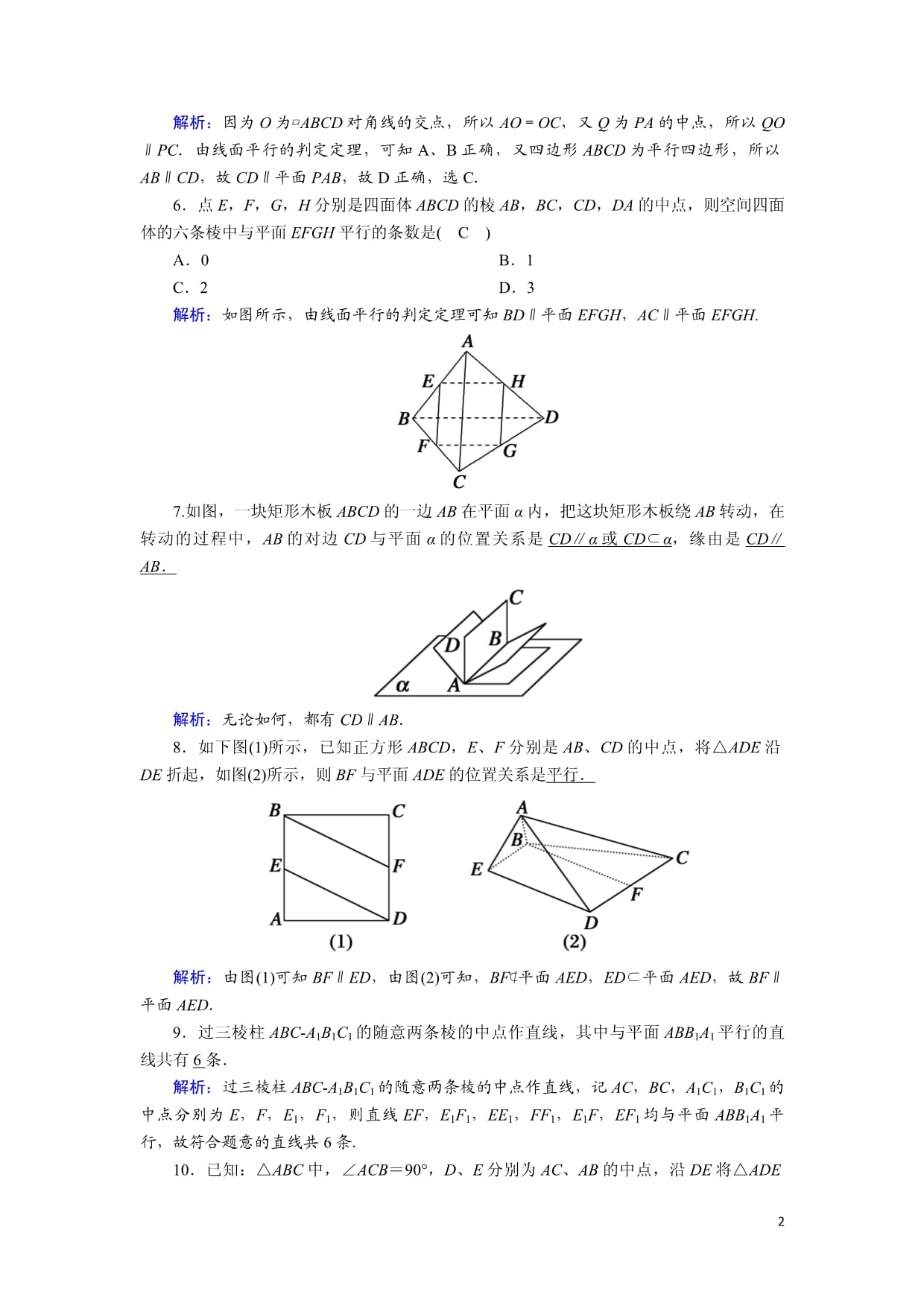
- 2. 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
- 3. 本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
- 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
- 5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
- 6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
- 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
最新文档
- 江西省吉安市新干县第二中学2025年高三第一次模拟考试化学试卷含解析
- 慢性肾病患者教育
- 宁夏回族自治区银川市长庆高级中学2025年高三一诊考试化学试卷含解析
- 2025年理线器合作协议书
- 2025届山东省济南市历城区济钢高级中学高三考前热身化学试卷含解析
- 护理品管圈的心得
- 河南省信阳市光山县第二高级中学2024-2025学年高一下学期3月第一次月考生物学试题(含答案)
- 2025年海南省省直辖县级行政单位琼中黎族苗族自治县中考一模历史试题(含答案)
- 2025年HITECOAT高耐蚀耐磨化学镀镍磷合金钢板材项目发展计划
- SYB甜品店创业计划书
- 掌握重点中职电子商务教师资格证试题与答案
- 5.3基本经济制度 课件 2024-2025学年统编版道德与法治八年级下册
- 河南省郑州市管城区2024-2025学年级九年级下学期第一次模拟数学试题(原卷版+解析版)
- 隔音涂料施工方案
- 甘肃卷2024年高考真题化学试题(含答案)
- T-CCTAS 61-2023 桥梁承重缆索抗火密封综合防护技术规程
- 消防员职业技能鉴定中级技能题库大全
- 铁路行车组织 课件 项目4 调车工作
- 2024年浙江邮电职业技术学院高职单招职业技能测验历年参考题库(频考版)含答案解析
- (一模)2024-2025学年佛山市普通高中教学质量检测(一)数学试卷(含答案)
- 招标代理机构选取突发情况应急处理预案

评论
0/150
提交评论