《等量关系》课件

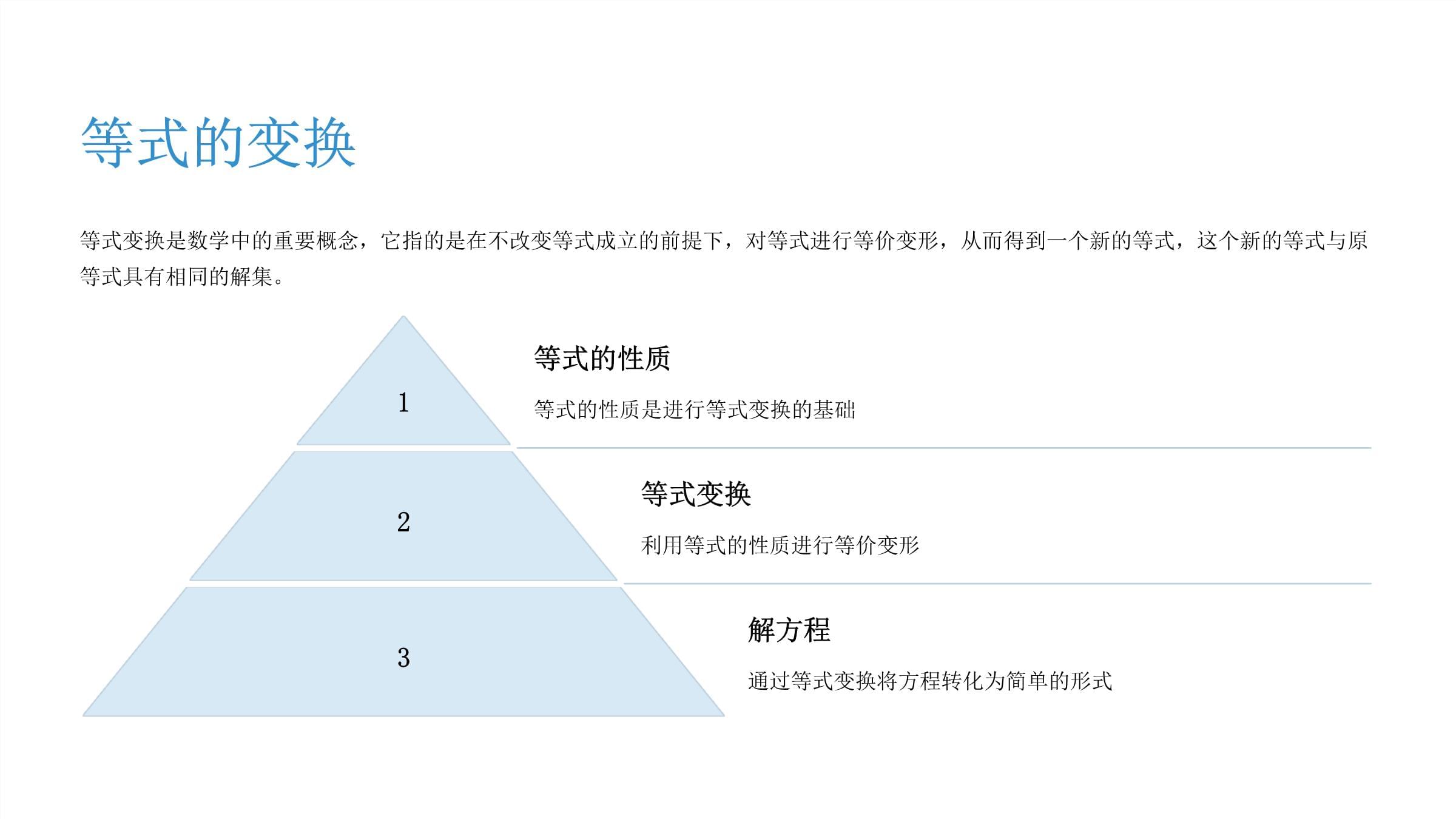
等量关系等量关系是数学中重要的基本概念。它描述了两个表达式或数量之间的相等关系。等量关系是什么平衡与对等等量关系表达两个事物或概念之间的平衡状态，它们在某种程度上相等或具有相同的价值。数量相等在数学领域，等量关系表示两个量值或表达式相等，例如，两个容器中液体体积相同。数学符号等量关系用等号“=”来表示，它表示等号两侧的表达式或值相等。等量关系的性质对称性如果a=b，那么b=a，也就是说，等号两边可以互换位置。例如，如果2+3=5，那么5=2+3。传递性如果a=b且b=c，那么a=c。也就是说，如果两个量相等，而第二个量又等于第三个量，那么第一个量也等于第三个量。例如，如果2+3=5且5=7-2，那么2+3=7-2。等式的性质对称性等式两边可以互换位置，等式仍然成立。传递性如果a=b且b=c，则a=c。加减性等式两边同时加上或减去同一个数或同一个式子，等式仍然成立。乘除性等式两边同时乘以或除以同一个不为零的数或同一个式子，等式仍然成立。等式的变换等式变换是数学中的重要概念，它指的是在不改变等式成立的前提下，对等式进行等价变形，从而得到一个新的等式，这个新的等式与原等式具有相同的解集。1等式的性质等式的性质是进行等式变换的基础2等式变换利用等式的性质进行等价变形3解方程通过等式变换将方程转化为简单的形式等式的移项1定义移项改变符号。2原则移项要改变符号。3目的将未知数放在一边。移项是解方程的重要步骤之一。它将等式中的某个项移到另一边，同时改变该项的符号。通过移项，可以将未知数集中到等式的一侧，从而方便求解方程。等式的合并1合并同类项将等式两边相同字母的项合并在一起，方便后续计算。2合并常数项将等式两边所有常数项合并在一起，简化等式结构。3化简等式合并同类项和常数项后，得到一个简化的等式，方便解题。等式的乘除等式两边同乘等式两边乘以同一个数，等式仍然成立。等式两边同除等式两边除以同一个非零数，等式仍然成立。注意事项除数不能为零乘除运算需要保持等式的平衡一元一次方程方程的定义等式中含有未知数的式子，称为方程一元一次方程只含有一个未知数，并且未知数的最高次数为1的方程，称为一元一次方程解方程求方程的解的过程，叫做解方程解一元一次方程的步骤1化简方程合并同类项，将所有包含未知数的项移到方程的一边，常数项移到另一边。2系数化为1将未知数的系数化为1，可以通过除以系数的方式实现。3解出未知数通过化简和系数化为1，得出未知数的值，即方程的解。简单实例演示等量关系是指两个表达式相等，用等号连接。例如：x+2=5，其中x+2和5表示相等的值。解方程就是求出未知数x的值，使等式成立。复杂实例演示例如，求解方程：2x+5=11。首先，移项，得到：2x=11-5=6。然后，系数化为1，得到：x=6÷2=3。因此，该方程的解为：x=3。等量公式总结1等量关系的核心等量公式是数学中表示等量关系的核心工具，它提供了对数量之间关系的精确描述。2等量公式的应用在解方程、化简表达式、证明定理等方面都发挥着重要作用。3等量公式的理解理解等量公式的关键在于理解等量关系的本质和应用。4等量公式的掌握熟练掌握等量公式是解决数学问题的关键，需要不断练习和应用。等量公式应用场景工程设计等量公式用于计算材料用量，确保结构强度和安全。金融市场等量公式用于分析市场趋势，预测投资收益和风险。科学研究等量公式用于建立物理模型，解释自然现象，进行科学实验。数学学习等量公式是数学解题的基础，用于解决各种数学问题。几何中的等量关系几何图形中，等量关系无处不在。例如，等边三角形的三条边长度相等，等腰三角形的两条腰长度相等。等量关系是几何证明的重要基础。通过等量关系，我们可以推出几何图形的性质和特征。代数中的等量关系代数中的等量关系是代数运算和方程的基础，它可以帮助我们理解和解决各种数学问题。在代数中，我们使用符号来表示未知数，例如x,y,z等，然后通过方程来建立变量之间的关系。等量关系在代数中扮演着至关重要的角色，它允许我们对等式进行一系列操作，从而解出未知数的值。等量关系在生活中的应用等量关系在日常生活中随处可见，比如购物时计算商品总价、烹饪时根据食谱调整食材比例、测量房屋面积等都运用到等量关系。通过等量关系，我们可以更准确地预测和控制事物的变化，使生活更便捷、高效。等量关系在科学研究中的应用等量关系在科学研究中发挥着至关重要的作用，帮助科学家进行精确测量、建立数学模型、推导出定理和规律。例如，牛顿万有引力定律、爱因斯坦的质能方程等物理定律都是基于等量关系建立的。在化学领域，化学方程式描述了化学反应中物质之间的定量关系，为合成新物质和研究物质性质提供了重要依据。等量关系的局限性非线性关系等量关系主要用于描述线性关系，对于非线性关系则无法准确表达。动态变化现实世界中许多事物处于动态变化中，等量关系难以反映这些动态变化。多因素影响许多问题受到多个因素的影响，等量关系往往无法完全涵盖所有影响因素。精确性局限等量关系是基于精确测量和计算的，但在现实世界中，测量和计算存在误差。等量关系发展历程1现代数学等量关系成为数学研究的核心2古代文明等量关系应用于测量和工程3古希腊欧几里得几何奠定基础等量关系的发展历程源远流长，从古代文明的测量和工程实践开始，到古希腊的欧几里得几何奠定了其基础。现代数学中，等量关系成为核心，它与其他数学分支相互影响，共同推动着数学的发展。等量关系与不等式等量关系等量关系表示两个表达式相等，用等号“=”连接。等量关系具有传递性、对称性、可加性和可乘性等性质。不等式不等式表示两个表达式不相等，用不等号“≠”连接。不等式分为大于号“>”、小于号“<”、大于等于号“≥”、小于等于号“≤”。等量关系与函数函数表达式函数关系可以用来表示等量关系，例如y=2x表示y的值是x值的2倍。函数变换等量关系的变换可以用函数图像的平移、缩放等操作来体现，例如将函数y=x平移2个单位得到y=x+2。数学模型函数可以用来建立现实问题的数学模型，等量关系则可以用函数方程的形式来描述。等量关系与极限11.极限概念极限是数学分析中的重要概念，它描述了函数或数列在趋近于某个点或无穷大时，其值的变化趋势。22.等量关系等量关系则描述了两个量之间相等的数学关系，它可以用来描述极限的性质。33.联系与区别极限的概念可以用来描述等量关系的变化趋势，而等量关系则可以用来描述极限的具体数值。44.应用场景极限和等量关系在微积分、物理学、工程学等领域都有着广泛的应用。等量关系的思维训练逻辑推理等量关系建立在逻辑推理的基础上，通过分析和判断，建立起等量关系。抽象思维等量关系通常涉及抽象的概念和符号，需要进行抽象思维，理解和应用等量关系。问题解决等量关系可以用来解决现实世界中的问题，需要将问题转化为等量关系，并进行求解。批判性思考在应用等量关系时，需要批判性思考，判断等量关系是否成立，以及是否符合实际情况。等量关系学习技巧11.理解概念深刻理解等量关系的定义和性质。22.多做练习通过大量的练习，掌握等量关系的应用技巧。33.联系实际将等量关系应用到生活实际问题中，加深理解。44.总结归纳总结常见的等量关系类型和解题方法。等量关系的教学方法概念理解首先，要确保学生理解“等量关系”的概念，通过生活实例和直观演示进行讲解，帮助学生建立概念理解。老师可以使用图像、模型、游戏等方式，将抽象的数学概念转化为学生能够理解的具体事物。练习与应用大量的练习可以帮助学生熟练掌握等量关系的知识和应用方法，通过练习可以发现学生在学习过程中的问题，及时进行指导和纠正。老师可以设计各种类型的练习题，包括基础题、提高题和应用题，以满足不同层次学生的学习需求。思维训练等量关系的学习需要逻辑推理和抽象思维能力，老师可以通过设计一些思考题、开放性问题，引导学生进行思考和分析，培养学生的逻辑思维能力。老师可以鼓励学生进行合作学习，共同解决问题，在学习过程中互相启发，共同进步。等量关系的发展趋势数据驱动等量关系在数据分析、机器学习等领域扮演重要角色，数据驱动模型的建立和验证。人工智能等量关系为人工智能的深度学习提供了理论基础，推动了人工智能技术的发展。量子计算量子计算可能改变等量关系的应用方式，带来新的理解和应用场景。等量关系的重要性数学基础等量关系是数学中的基础概念，贯穿整个数学体系。科学研究科学研究中大量使用等量关系来分析数据，建立模型，进行推演。工程设计工程师在设计桥梁、建筑等工程时，需要运用等量关系来确保结构安全、稳定。经济分析经济学家使用等量关系来分析经济数据，预测市场趋势，制定经济政策。等量关系的思考与展望深入研究等量关系在各个领域都具有重要的应用价值。需要不断深入研究其本质，探索更广阔的应用前景。跨学科融合将等量关系与其他学科进行