二次函数图象及性质课件

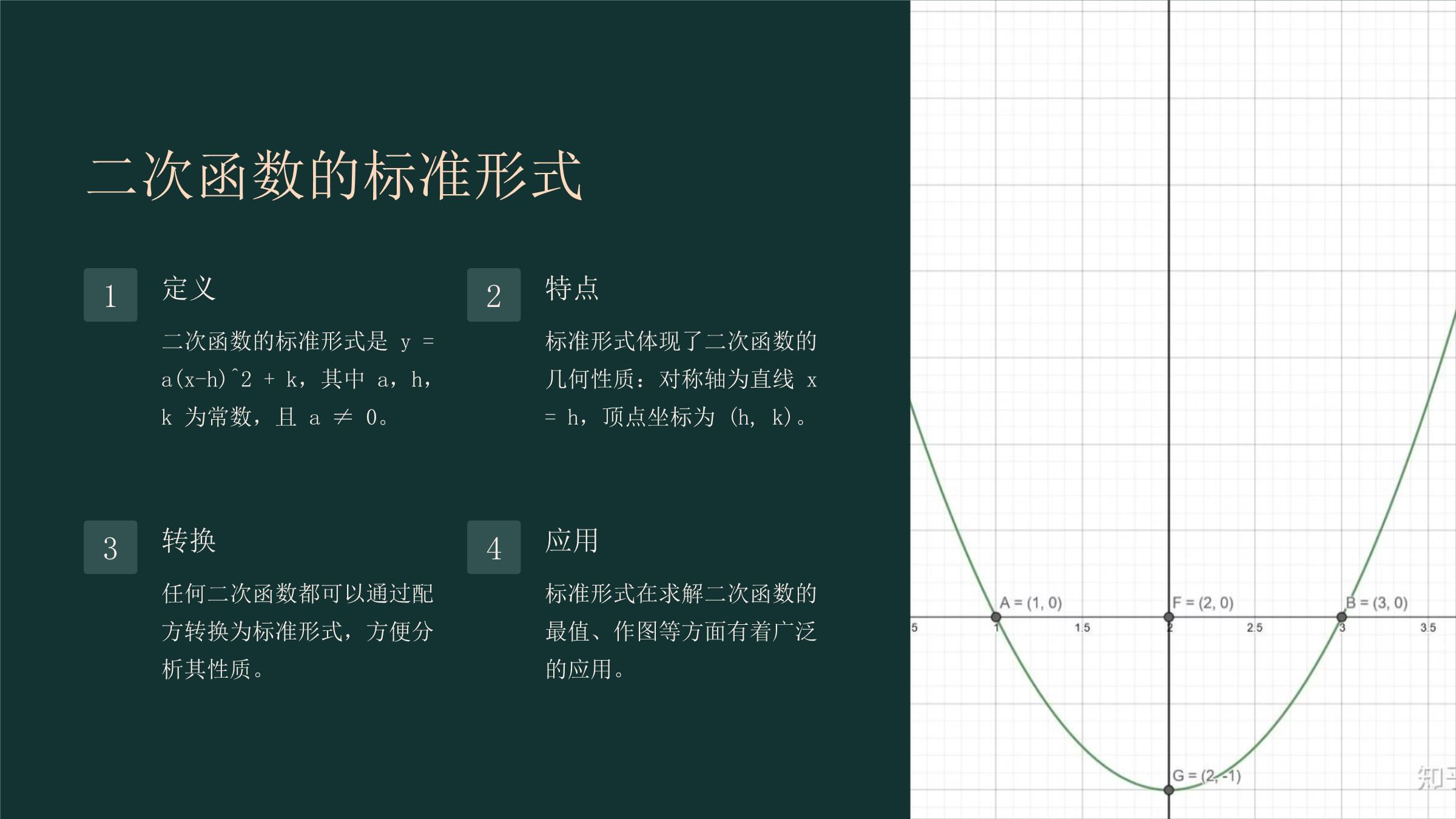
二次函数图象及性质二次函数是数学中重要的函数类型之一，在现实生活中有着广泛的应用，例如抛物线轨迹、桥梁设计等。通过研究二次函数的图象和性质，我们可以更好地理解二次函数的特征，并将其应用于解决实际问题。二次函数的定义定义二次函数是指形如y=ax²+bx+c(a≠0)的函数。其中，a，b，c是常数，x是自变量，y是因变量。特点二次函数的图象是抛物线，其开口方向取决于a的符号：a>0时开口向上，a<0时开口向下。应用二次函数在物理学、工程学、经济学等领域有着广泛的应用，例如，描述物体运动轨迹、研究成本利润关系、分析经济增长趋势等。二次函数的标准形式1定义二次函数的标准形式是y=a(x-h)^2+k，其中a，h，k为常数，且a≠0。2特点标准形式体现了二次函数的几何性质：对称轴为直线x=h，顶点坐标为(h,k)。3转换任何二次函数都可以通过配方转换为标准形式，方便分析其性质。4应用标准形式在求解二次函数的最值、作图等方面有着广泛的应用。二次函数图象的对称轴和顶点对称轴二次函数图象的对称轴是一条直线，它将图象分成两部分，这两部分关于对称轴对称。顶点二次函数图象的顶点是图象上最高或最低的点，它位于对称轴上。顶点坐标公式二次函数图象的顶点坐标可以通过公式计算得出，公式为(-b/2a,f(-b/2a))。二次函数图象的开口方向开口向上二次项系数a大于0时，抛物线开口向上。开口向下二次项系数a小于0时，抛物线开口向下。二次函数图象的轴对称二次函数图象关于其对称轴对称。对称轴是一条垂直于x轴的直线，它将图象分成两个完全相同的镜像部分。对称轴的方程可以用顶点坐标来确定，它可以用来确定图象上任意一点关于对称轴的对称点。二次函数图象的性质开口方向二次函数图象的开口方向取决于二次项系数的正负号，正数则开口向上，负数则开口向下。对称轴二次函数图象的对称轴是一条垂直于x轴的直线，其方程为x=-b/2a。顶点顶点是二次函数图象的最高点或最低点，其坐标为(-b/2a,f(-b/2a))。单调性二次函数图象在对称轴左侧单调递增，在对称轴右侧单调递减。二次函数的极值及判定极值的概念二次函数的极值是指函数在某个点取得的最大值或最小值。顶点坐标二次函数的极值点就是其图象的顶点，其坐标为(-b/2a,f(-b/2a))。开口方向如果二次函数开口向上(a>0)，则顶点为最小值点；如果开口向下(a<0)，则顶点为最大值点。判定方法通过判断二次函数的开口方向和顶点坐标来确定极值类型和值。二次函数的零点及判定1定义二次函数图像与x轴的交点称为函数的零点，即使函数值为零的自变量的值。2判定方法可以通过解二次方程求解，也可以利用图像观察函数图像与x轴的交点。3应用二次函数的零点可以用于解决实际问题，例如求解抛物线的最大高度或最小高度。二次函数的判别式判别式公式二次函数判别式为△=b²-4ac，其中a，b，c分别为二次函数ax²+bx+c=0中的系数。判别式作用判别式用于判断二次函数的根的情况：△>0有两个不相等的实根，△=0有两个相等的实根，△<0没有实根。应用判别式在实际问题中可以用来判断方程是否有解，例如求解物理模型中的未知参数。二次函数的应用实例二次函数在生活中应用广泛，例如抛物线形状的拱桥、桥梁的设计和建造。二次函数可以描述物体在重力作用下的运动轨迹，例如足球在空中飞行的轨迹。二次函数的实际应用抛物线运动足球运动员踢出的足球、跳水运动员入水时形成的抛物线，这些现象都可以用二次函数来描述。建筑设计建筑师在设计拱桥、房屋的屋顶时，会利用二次函数的性质来保证结构的稳定性。工程技术工程师在设计电路、管道、桥梁时，会运用二次函数来优化结构，提高效率。最大值和最小值应用问题1建模将实际问题转化为数学模型2求解利用二次函数性质求解模型3解释将数学解转化为实际问题答案最大值和最小值问题是现实生活中常见问题，例如求利润最大化、成本最小化、面积最大化等。通过将实际问题转化为二次函数模型，利用二次函数性质求解最大值或最小值，最终得到实际问题的答案。优化问题的建模与求解1问题分析明确目标函数和约束条件。2模型建立将实际问题转化为数学模型。3求解模型运用数学方法求解最优解。4结果验证验证模型的有效性和解的合理性。二次函数画图的注意事项确定开口方向根据二次项系数判断，正数开口向上，负数开口向下。求对称轴和顶点对称轴是直线x=-b/2a，顶点坐标为(-b/2a,f(-b/2a))。选择合适点除了顶点外，还可以选择几个特殊点，例如x轴上的交点，y轴上的交点，以及对称轴上的点。连接并平滑根据选取的点，连接成一个平滑的抛物线，注意开口方向和顶点位置。二次函数图象的综合运用通过对二次函数图象和性质的深入理解，我们可以将其应用于解决实际问题。例如，我们可以利用二次函数求解最大值或最小值，并将其应用于优化问题。二次函数的性质总结图象性质开口方向、对称轴、顶点坐标、单调性、最值、零点等。表达式性质一次项系数决定开口方向，常数项决定纵截距，顶点坐标与对称轴关系等。函数性质定义域、值域、奇偶性、周期性、单调性、最值等。二次函数在生活中的应用抛物线形状桥梁、拱门、卫星天线等结构常利用抛物线的形状，能使结构更坚固、稳定，并能有效地利用空间。最佳路径许多现实生活中需要找到最短路径、最省时间或最省成本的应用，都可以通过二次函数模型来解决。经济决策二次函数模型可用于分析成本、利润、收益等经济指标之间的关系，帮助企业制定最佳的生产和经营策略。二次函数在工程技术中的应用桥梁建设二次函数可用于桥梁拱形的建模，确保结构稳定性。航空工程二次函数可用于飞机轨迹的优化，提高飞行效率。卫星天线二次函数可用于设计卫星天线形状，提高信号接收效率。机器人设计二次函数可用于机器人关节运动的控制，实现精确运动。二次函数在经济决策中的应用成本效益分析用二次函数模型分析成本和收益之间的关系，找到最佳生产规模或投资方案，最大限度地提高经济效益。价格策略利用二次函数模型预测产品需求量，制定合理的价格策略，平衡供需关系，实现利润最大化。市场预测通过分析历史数据，建立二次函数模型，预测未来市场需求的变化趋势，为企业决策提供参考。资源配置根据二次函数模型，优化资源配置方案，提高效率，降低成本，最大限度地利用有限的资源。二次函数在交通运输中的应用桥梁设计二次函数可用于桥梁设计，例如抛物线桥拱的形状。道路规划高速公路和铁路的弯道设计，利用二次函数可以确定最佳曲线半径。减速带设计减速带的形状通常采用二次函数曲线，确保车辆减速平稳。信号灯控制交通信号灯的控制系统可以使用二次函数模型，优化交通流量。二次函数在物理学中的应用抛射运动抛射运动遵循抛物线轨迹，可以使用二次函数来描述其运动规律。简谐运动弹簧振子和单摆的运动都可以用二次函数来描述，其位移和时间的关系呈周期性变化。自由落体运动自由落体运动的距离与时间平方成正比，可以用二次函数来表示，并推导出加速度公式。二次函数在化学中的应用化学反应速率化学反应速率通常可以用二次函数来描述。可以通过二次函数模型来预测反应速率随时间变化的趋势。物质浓度变化二次函数可以用来模拟化学反应中物质浓度的变化，例如反应物浓度随时间的变化规律。二次函数在生物学中的应用植物生长二次函数可用于模拟植物生长曲线，预测植物的生长速度和最终高度。DNA结构二次函数可用来描述DNA分子的螺旋结构，并分析其稳定性。种群增长二次函数可用于建立种群增长模型，预测种群数量的变化趋势。细菌繁殖二次函数可以模拟细菌繁殖的指数增长，预测细菌数量的变化。二次函数在心理学中的应用学习曲线二次函数可以模拟学习过程，随着时间的推移，学习效率先提高，然后逐渐下降。认知偏差二次函数可以描述认知偏差，例如，人们对损失的敏感程度往往高于对收益的敏感程度。心理测量二次函数可以用于心理测量，例如，建立心理测试的评分标准和进行心理评估。二次函数在管理学中的应用利润最大化企业通常使用二次函数模型来分析成本和收益，确定最佳生产规模，从而实现利润最大化。库存管理二次函数可以用于建立库存模型，帮助企业确定最佳库存水平，降低库存成本，提高效率。市场需求预测通过分析市场需求数据，利用二次函数模型，可以预测未来市场需求趋势，制定更有效的营销策略。人力资源优化二次函数模型可用于员工招聘、培训和薪酬管理等方面，帮助企业优化人力资源配置，提高工作效率。二次函数在艺术设计中的应用1曲线美二次函数的曲线形状优美，可以用在建筑设计、绘画和雕塑等艺术领域中。2比例与平衡二次函数可以帮助艺术家精确地控制比例和平衡，创作出和谐美观的艺术作品。3动态与韵律二次函数的曲线可以营造出一种动态和韵律感，为作品增添活力。4抽象艺术二次函数的图形可以作为抽象艺术的创作元素，展现艺术家对数学与美学的独特理解。二次函数在建筑设计中的应用拱形结构二次函数曲线可以精确描述拱形结构的形状，帮助设计师设计稳固、优美的建筑。例如，桥梁、体育场和建筑物屋顶的拱形结构应用了二次函数的原理。曲线型外墙二次函数曲线可以应用于建筑外墙的设计，创造出具有流线型和现代感的建筑效果。例如，博物馆、艺术中心和住宅建筑的外墙设计常常采用二次函数曲线，增添建筑的艺术性和现代感。二次函数在环境保护中的应用空气污染控制二次函数模型可以用来预测空气污染物的浓度变化，帮助制定污染控制措施，例如优化排放标准和制定污染排放限值。水污染治理二次函数模型可以用来模拟水体污染物的扩散和降解过程，帮助制定