专题17 二次函数性质综合（原卷版）

专题17二次函数性质综合1．（2023·湖南·统考中考真题）如图所示，直线l为二次函数的图像的对称轴，则下列说法正确的是（

）

A．b恒大于0 B．a，b同号 C．a，b异号 D．以上说法都不对2．（2023·甘肃兰州·统考中考真题）已知二次函数，下列说法正确的是（

）A．对称轴为B．顶点坐标为C．函数的最大值是－3D．函数的最小值是－33．（2023·广西·统考中考真题）将抛物线向右平移3个单位，再向上平移4个单位，得到的抛物线是（

）A． B．C． D．4.（2022·新疆）已知抛物线，下列结论错误的是（

）A．抛物线开口向上 B．抛物线的对称轴为直线 C．抛物线的顶点坐标为 D．当时，y随x的增大而增大5．（2023·辽宁大连·统考中考真题）已知抛物线，则当时，函数的最大值为（

）A． B． C．0 D．26.（2022·陕西）已知二次函数y=x2−2x−3的自变量x1，x2，x3对应的函数值分别为y1，y2，y3．当−1<x1<0，1<x2<2，x3>3时，y1，y2，y3三者之间的大小关系是（

）A． B． C． D．7．（2023·四川成都·统考中考真题）如图，二次函数的图象与x轴交于，两点，下列说法正确的是（

）

A．抛物线的对称轴为直线 B．抛物线的顶点坐标为C．，两点之间的距离为 D．当时，的值随值的增大而增大8．（2022·浙江宁波）点A（m-1，y1），B（m，y2）都在二次函数y=（x-1）2+n的图象上．若y1＜y2，则m的取值范围为（

）A． B． C． D．9．（2023·河南·统考中考真题）二次函数的图象如图所示，则一次函数的图象一定不经过（

）

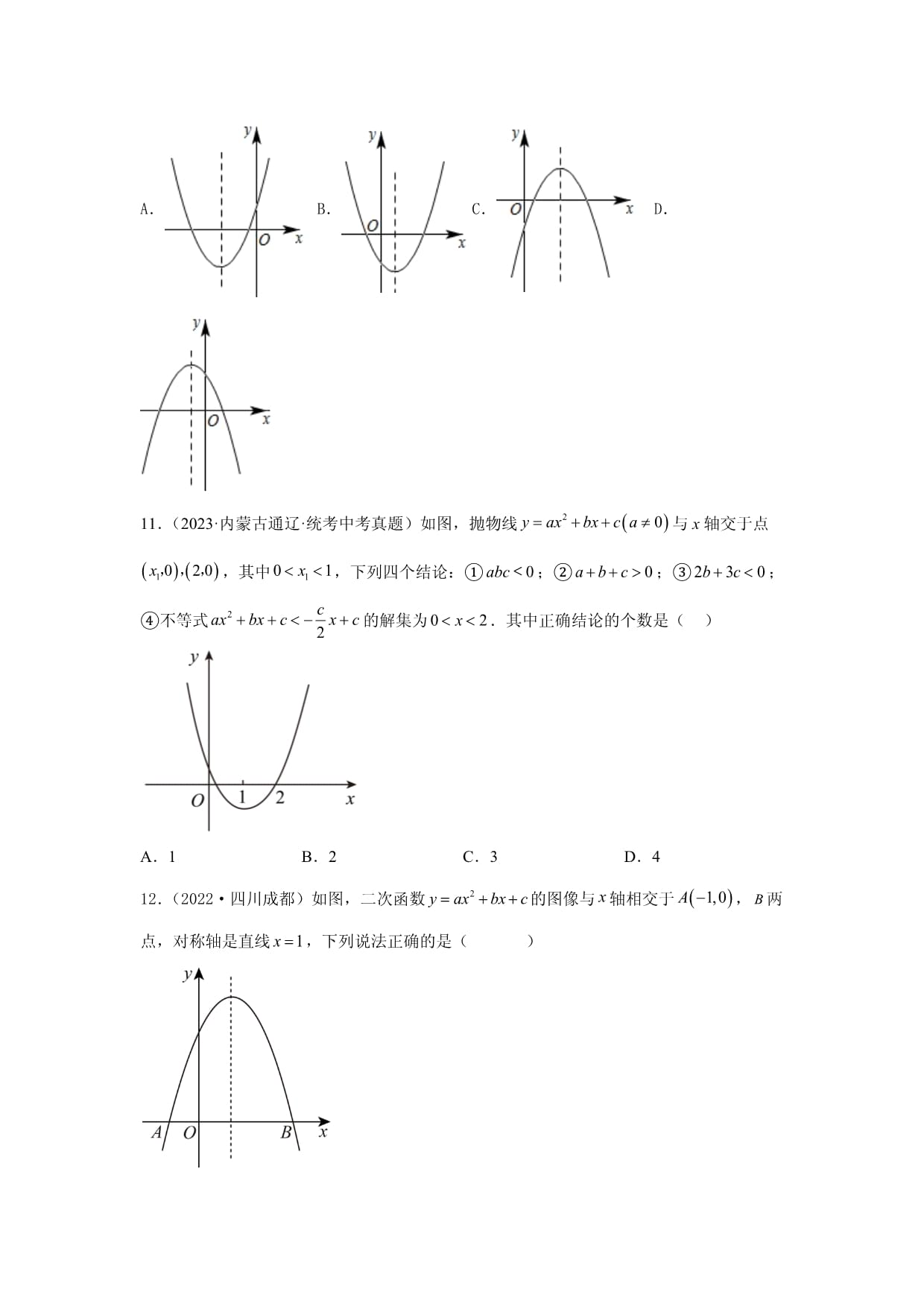
A．第一象限 B．第二象限 C．第三象限 D．第四象限10．（2022·湖南株洲）已知二次函数，其中、，则该函数的图象可能为（

）A．B．C．D．11．（2023·内蒙古通辽·统考中考真题）如图，抛物线与x轴交于点，其中，下列四个结论：①；②；③；④不等式的解集为．其中正确结论的个数是（

）

A．1 B．2 C．3 D．412．（2022·四川成都）如图，二次函数的图像与轴相交于，两点，对称轴是直线，下列说法正确的是（

）A． B．当时，的值随值的增大而增大C．点的坐标为 D．13.（2022·湖北随州）如图，已知开口向下的抛物线与x轴交于点对称轴为直线．则下列结论：①；②；③函数的最大值为；④若关于x的方数无实数根，则．正确的有（

）A．1个 B．2个 C．3个 D．4个14.（2022·天津）已知抛物线（a，b，c是常数，）经过点，有下列结论：①；②当时，y随x的增大而增大；③关于x的方程有两个不相等的实数根．其中，正确结论的个数是（

）A．0 B．1 C．2 D．315．（2023·四川自贡·统考中考真题）经过两点的抛物线（为自变量）与轴有交点，则线段长为（

）A．10 B．12 C．13 D．1516．（2023·四川达州·统考中考真题）如图，拋物线（为常数）关于直线对称．下列五个结论：①；②；③；④；⑤．其中正确的有（

）

A．4个 B．3个 C．2个 D．1个17.（2021·四川凉山彝族自治州·中考真题）二次函数的图象如图所示，则下列结论中不正确的是（）A． B．函数的最大值为C．当时， D．18．（2023·四川泸州·统考中考真题）已知二次函数（其中是自变量），当时对应的函数值均为正数，则的取值范围为（）A． B．或C．或 D．或19.（2021·江苏苏州市·中考真题）已知抛物线的对称轴在轴右侧，现将该抛物线先向右平移3个单位长度，再向上平移1个单位长度后，得到的抛物线正好经过坐标原点，则的值是（）A．或2 B． C．2 D．20．（2023·四川南充·统考中考真题）抛物线与x轴的一个交点为，若，则实数的取值范围是(

)A． B．或C． D．或21．（2021·四川遂宁市·中考真题）已知二次函数的图象如图所示，有下列5个结论：①；②；③；④（）；⑤若方程＝1有四个根，则这四个根的和为2，其中正确的结论有（）A．2个 B．3个 C．4个 D．5个22．（2023·安徽·统考中考真题）已知反比例函数在第一象限内的图象与一次函数的图象如图所示，则函数的图象可能为（

）

A．

B．

C．

D．

23.（2021·陕西中考真题）下表中列出的是一个二次函数的自变量x与函数y的几组对应值：…-2013……6-4-6-4…下列各选项中，正确的是A．这个函数的图象开口向下B．这个函数的图象与x轴无交点C．这个函数的最小值小于-6D．当时，y的值随x值的增大而增大24．（2023·四川广安·统考中考真题）如图所示，二次函数为常数，的图象与轴交于点．有下列结论：①；②若点和均在抛物线上，则；③；④．其中正确的有（）

A．1个 B．2个 C．3个 D．4个25．（2023·四川眉山·统考中考真题）如图，二次函数的图象与x轴的一个交点坐标为，对称轴为直线，下列四个结论：①；②；③；④当时，；其中正确结论的个数为（

）

A．1个 B．2个 C．3个 D．4个26．（2023·新疆·统考中考真题）如图，在平面直角坐标系中，直线与抛物线相交于点，．结合图象，判断下列结论：①当时，；②是方程的一个解；③若，是抛物线上的两点，则；④对于抛物线，，当时，的取值范围是．其中正确结论的个数是（

）

A．4个 B．3个 C．2个 D．1个27．（2023·四川乐山·统考中考真题）如图，抛物线经过点，且，有下列结论：①；②；③；④若点在抛物线上，则．其中，正确的结论有（

）

A．4个 B．3个 C．2个 D．1个28．（2023·湖北随州·统考中考真题）如图，已知开口向下的抛物线与x轴交于点，对称轴为直线．则下列结论正确的有（

）①；②；③方程的两个根为；④抛物线上有两点和，若且，则．

A．1个 B．2个 C．3个 D．4个29．（2023·湖北·统考中考真题）拋物线与轴相交于点．下列结论：①；②；③；④若点在抛物线上，且，则．其中正确的结论有(

)A．1个 B．2个 C．3个 D．4个30．（2023·湖南郴州·统考中考真题）抛物线与轴只有一个交点，则________．31．（2023·福建·统考中考真题）已知抛物线经过两点，若分别位于抛物线对称轴的两侧，且，则的取值范围是___________．32.（2021·山东泰安市·中考真题）如图是抛物线的部分图象，图象过点，对称轴为直线，有下列四个结论：①；②；③y的最大值为3；④方程有实数根．其中正确的为________（将所有正确结论的序号都填入）．33．（2023·内蒙古·统考中考真题）已知二次函数，若点在该函数的图象上，且，则的值为________．34.（2021·安徽）设抛物线，其中a为实数．（1）若抛物线经过点，则______；（2）将抛物线向上平移2个单位，所得抛物线顶点的纵坐标的最大值是______．35.（2021·湖北武汉市·中考真题）已知抛物线（，，是常数），，下列四个结论：①若抛物线经过点，则；②若，则方程一定有根；③抛物线与轴一定有两个不同的公共点；④点，在抛物线上，若，则当时，．其中正确的是__________（填写序号）．36．（2023·湖北武汉·统考中考真题）抛物线（是常数，）经过三点，且．下列四个结论：①；②；③当时，若点在该抛物线上，则；④若关于的一元二次方程有两个相等的实数根，则．其中正确的是________（填写序号）．37.（2020·内蒙古中考真题）在平面直角坐标系中，已知和是抛物线上的两点，将抛物线的图象向上平移n（n是正整数）个单位，使平移后的图象与x轴没有交点，则n的最小值为_____．38.（2020·湖北荆门?中考真题）如图，抛物线与x轴交于点A、B，顶点为C，对称轴为直线，给出下列结论：①；②若点C的坐标为，则的面积可以等于2；③是抛物线上两点，若，则；④若抛物线经过点，则方程的两根为，3其中正确结论的序号为_______．39.（2020·湖北武汉?中考真题）抛物线（，，为常数，）经过，两点，下列四个结论：①一元二次方程的根为，；②若点，在该抛物线上，则；③对于任意实数，总有；④对于的每一个确定值，若一元二次方程（为常数，）的根为整数，则的值只有两个．其中正确的结论是________（填写序号）．40.（2021·浙江宁波市·中考真题）如图，二次函数（a为常数）的图象的对称轴为直线．（1）求a的值．（2）向下平移该二次函数的图象，使其经过原点，求平移后图象所对应的二次函数的表达式．41．（2023·浙江宁波·统考中考真题）如图，已知二次函数图象经过点和．

(1)求该二次函数的表达式及图象的顶点坐标．(2)当时，请根据图象直接写出x的取值范围．42.（2022·浙江嘉兴）已知抛物线L1：y＝a(x＋1)2－4（a≠0）经过点A(1，0)．(1)求抛物线L1的函数表达式．(2)将抛物线L1向上平移m（m＞0）个单位得到抛物线L2．若抛物线L2的顶点关于坐标原点O的对称点在抛物线L1上，求m的值．(3)把抛物线L1向右平移n（n＞0）个单位得到抛物线L3，若点B(1，y1)，C(3，y2)在抛物线L3上，且y1＞y2，求n的取值范围．43.（2022·浙江杭州）设二次函数（b，c是常数）的图像与x轴交于A，B两点．(1)若A，B两点的坐标分别为(1，0)，(2，0)，求函数的表达式及其图像的对称轴．(2)若函数的表达式可以写成（h是常数）的形式，求的最小值．(3)设一次函数（m是常数）．若函数的表达式还可以写成的形式，当函数的图像经过点时，求的值．44.（2022·浙江绍兴）已知函数（b，c为常数）的图象经过点（0，﹣3），（﹣6，﹣3）．(1)求b，c的值．(2)当﹣4≤x≤0时，求y的最大值．(3)当m≤x≤0时，若y的最大值与最小值之和为2，求m的值．45.（2022·浙江舟山）已知抛物线：（）经过点．(1)求抛物的函数表达式．(2)将抛物线向上平移m（）个单位得到抛物线．若抛物线的顶点关于坐标原点O的对称点在抛物线上，求m的