专题252圆与圆的位置关系-

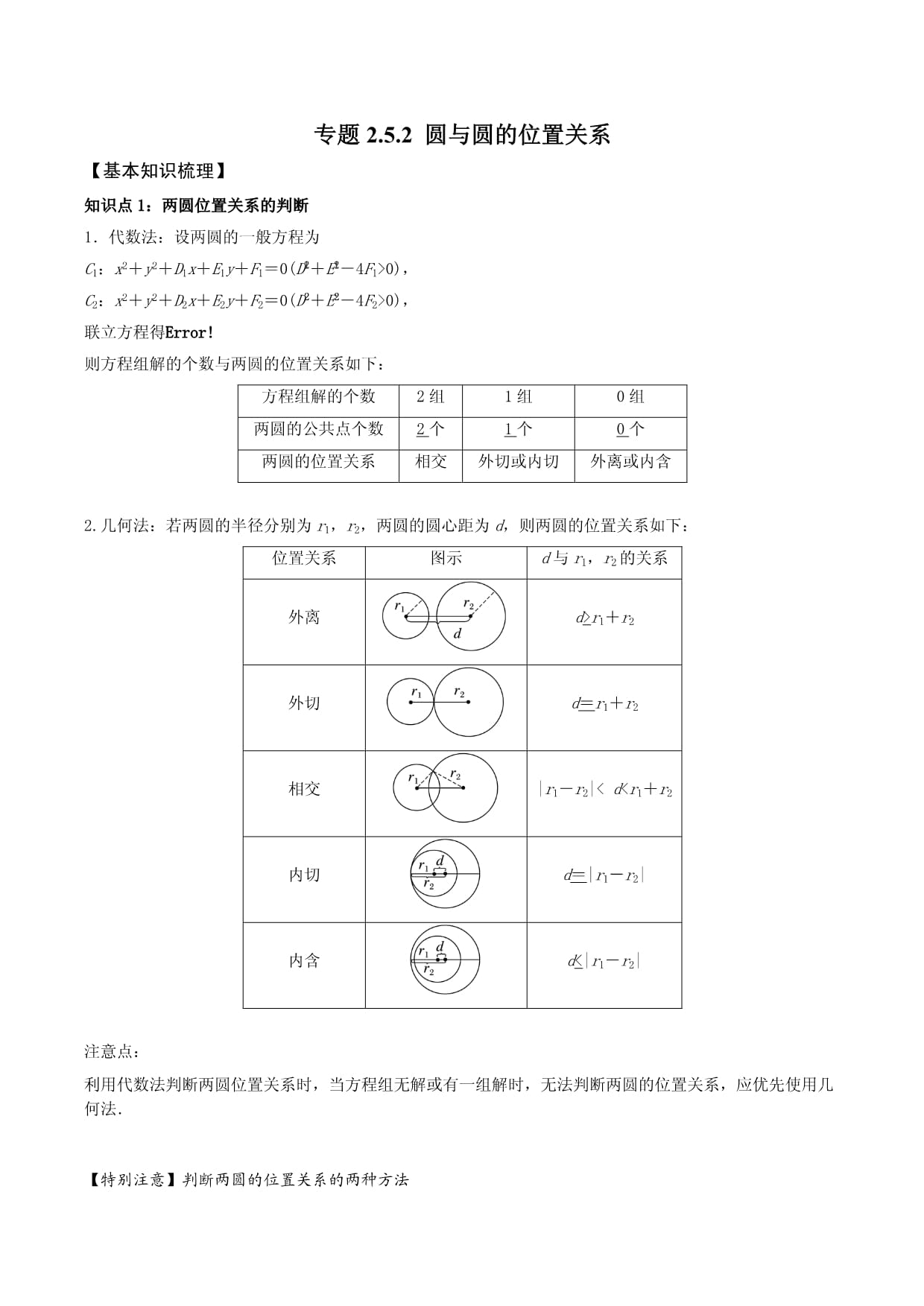
专题2.5.2圆与圆的位置关系【基本知识梳理】知识点1：两圆位置关系的判断1．代数法：设两圆的一般方程为C1：x2＋y2＋D1x＋E1y＋F1＝0(Deq\o\al(2,1)＋Eeq\o\al(2,1)－4F1>0)，C2：x2＋y2＋D2x＋E2y＋F2＝0(Deq\o\al(2,2)＋Eeq\o\al(2,2)－4F2>0)，联立方程得eq\b\lc\{\rc\(\a\vs4\al\co1(x2＋y2＋D1x＋E1y＋F1＝0，,x2＋y2＋D2x＋E2y＋F2＝0，))则方程组解的个数与两圆的位置关系如下：方程组解的个数2组1组0组两圆的公共点个数2个1个0个两圆的位置关系相交外切或内切外离或内含2.几何法：若两圆的半径分别为r1，r2，两圆的圆心距为d，则两圆的位置关系如下：位置关系图示d与r1，r2的关系外离d>r1＋r2外切d＝r1＋r2相交|r1－r2|<d<r1＋r2内切d＝|r1－r2|内含d<|r1－r2|注意点：利用代数法判断两圆位置关系时，当方程组无解或有一组解时，无法判断两圆的位置关系，应优先使用几何法．【特别注意】判断两圆的位置关系的两种方法(1)几何法：将两圆的圆心距d与两圆的半径之差的绝对值、半径之和进行比较，进而判断出两圆的位置关系，这是解析几何中主要使用的方法．(2)代数法：将两圆的方程组成方程组，通过解方程组，根据方程组解的个数进而判断两圆的位置关系．知识点2：相交弦问题(1)若圆C1：x2＋y2＋D1x＋E1y＋F1＝0与圆C2：x2＋y2＋D2x＋E2y＋F2＝0相交，则两圆公共弦所在的直线方程为(D1－D2)x＋(E1－E2)y＋F1－F2＝0.(2)公共弦长的求法①代数法：将两圆的方程联立，解出交点坐标，利用两点间的距离公式求出弦长．②几何法：求出公共弦所在直线的方程，利用圆的半径、半弦长、弦心距构成的直角三角形，根据勾股定理求解．【题型1圆与圆的位置关系的判定】【例1】（20232024·山东潍坊·高二上·期中）已知圆：，圆：，则与的位置关系是（）A.外切 B.内切 C.外离 D.相交【答案】D【解析】【分析】根据方程确定出圆心和半径，然后根据圆心距和半径的关系进行判断.【详解】因为的圆心为，半径，的圆心为，半径，所以，所以，所以与两圆相交，故选：D.【变式11】（20232024·上海·高二上·阶段测试）圆与圆的位置关系是A．内切 B．外切 C．相离 D．相交【答案】D【变式12】（20232024·浙江湖州·高二上·期末）已知圆：（，）与圆：，则圆与圆的位置关系是（）A.相交 B.相切 C.外离 D.与m的取值有关【答案】C【解析】【分析】求出两圆心距离，判断其与两圆半径和的大小即可得答案.【详解】圆：，即，圆心，半径，圆：，即，圆心，半径，所以当时，所以圆与圆的位置关系是外离.故选：C.【变式13】（20232024·山东·高二上·联考）（多选）已知圆，圆，则（

）A．直线与直线垂直B．与没有公共点C．与的位置关系为外离D．若分别为圆与圆上的动点，则的最大值为【答案】BD【分析】求出两圆的圆心及半径，求出即可判断A；求出圆心距即可判断BC；根据的最大值为即可判断D.【详解】由题意可知圆，则圆心，半径，圆，则圆心，半径，则，与直线不垂直，故A不正确；因为，所以与的位置关系为内含，故B正确，C不正确；对于D，的最大值为，故D正确.故选：BD.【题型2由圆与圆的位置关系确定参数】【例2】（20232024·浙江温州·高二上·期末）（多选）已知圆和圆外离，则整数m的一个取值可以是（）A.4 B.5 C.6 D.7【答案】CD【解析】【分析】写出两圆的圆心及半径，利用两点之间坐标公式求出圆心距，利用两圆外离的关系列出不等式，求出整数的值.【详解】因为方程可化为，所以圆的圆心的坐标为，半径为，因为方程可化为，由已知，且为正整数，所以圆的圆心的坐标为，半径为，所以圆心距，因为圆和圆外离，所以，所以，故的可能取值有，故选：CD.【变式21】（20232024·山东菏泽·高二上·期中）若圆与圆相切，则a的值为___________.【答案】或或【解析】【分析】讨论两圆为内切或外切两种情况，利用圆心距离与两圆半径的关系列方程求参数a即可.【详解】由的圆心为，半径为1；的圆心为，半径为5，∴若两圆内切，则，即；若两圆外切，则，即.故答案为：或或.【变式22】（20232024·四川眉山·高二上·期中）已知圆M:x2+y2=1和A．3 B．32 C．5 D．【解题思路】根据圆与圆的位置关系进行求解即可.【解答过程】因为圆M:x2+所以两圆相交或者相内切或者相外切，即m−1≤解得3≤m≤5，选项ABC满足，m的值不能为D.故选：D.【变式23】（20222023·山东潍坊·高二上·期中）（多选）已知圆与圆，则下列结论正确的是（

）A．若两圆外离，则的取值范围是B．当时，两圆内切C．若两圆相交，则的取值范围是D．当时，两圆相交于两点，此时相交弦的长为【答案】BC【分析】A、B、C项分别由圆与圆的位置关系对应的几何表达式求解.D项相交两圆的公共弦所在的直线方程为两圆方程之差，再由圆内的弦长公式可得结果.【详解】设：即：∴，即：∴圆心，半径为设：∴圆心，半径为∴圆心距，，对于A项，∵两圆外离∴

∴A项错误；对于B项，∵∴∴∴两圆内切.

∴B项正确；对于C项，∵两圆相交∴解得：

∴C项正确.对于D项，∵∴：∵AB所在的直线方程为两圆方程之差.∴AB所在的直线方程为∴∴

∴D项错误.故选：BC.【题型3两圆的公切线方程或条数】【例3】（20232024·江苏宿迁·高二上·期中）圆：与圆：的公切线条数为（）A.1 B.2 C.3 D.4【答案】B【解析】【分析】根据两圆的标准方程，判断出两圆的位置关系，即可得出结果.【详解】因为圆：的圆心为，，圆：的圆心为，，所以，可得，故圆与圆相交，所以圆与圆的公切线条数为2条，故选：B.【变式31】（20232024·湖北·高二上·期中）若圆与圆恰有一条公切线，则（）A．4 B．6 C．4或6 D．8【答案】B圆，圆与圆内切，，∴【变式32】（20232024·四川雅安·高二上·联考）（多选）圆与圆的公切线的方程可能为（）A. B.C. D.【答案】CD【解析】【分析】根据圆心距和半径的关系可判断两圆相交，结合圆的半径相等，可得切线斜率，即可由点到直线的距离公式求解.【详解】圆的圆心为，半径为，圆的圆心为，半径，由题意得，圆与圆的半径之和为，半径之差为0，因为，所以圆与圆的位置关系为相交．由题意得，因为圆与圆的半径相等，所以公切线的斜率为2．设公切线的方程为，即，由，得，所以公切线的方程为或．故选：CD【变式33】（20232024·河南郑州·高二上·期末）写出圆：与圆：的一条公切线方程________.【答案】写出或或一条即可【题型4相交圆的公共弦方程、公共弦长】【例4】（20232024·重庆·高二上·期中）（多选）已知圆和圆相交于两点，下列说法正确的为（）A.两圆外切 B.两圆有两条公切线C.直线的方程为 D.线段的长为【答案】BD【解析】【分析】对于A：根据题意可得两圆的圆心和半径，进而判断两圆的位置关系为相交；对于B：根据两圆相交分析判断；对于C：根据两圆方程之差即为公共弦所在直线方程，运算求解即可；对于D：利用点到直线的距离公式结合垂径定理求公共弦长.【详解】由题意可知：圆的圆心，半径，圆，即，可知圆心，半径，对于选项A：因为，则，所以两圆相交，故A错误；对于选项B：因为两圆相交，所以两圆有两条公切线，故B正确；对于选项C：因为两圆相交，则两圆方程之差即为公共弦所在直线方程，可得直线的方程为，故C错误；对于选项D：因为到直线的距离，所以线段的长为，故D正确；故选：BD.【变式41】（20232024·陕西西安·高二上·期中）已知圆，圆，则下列选项错误的是（）A.两圆的圆心距离是 B.两圆有条公切线C.两圆相交 D.公共弦长【答案】D【变式42】（20232024·山东青岛·高二上·期中）（多选）已知圆与圆，下列说法正确的是（）A.与的公切线恰有4条B.与相交弦的方程为C.与相交弦的弦长为D.若，分别是圆，上的动点，则【答案】BCD【解析】【分析】求出圆心距，判断两圆位置关系即可判断A；两圆方程相减消去二次项可判断B；利用点到直线的距离公式求到相交弦的距离，然后由弦长公式求弦长可判断C；观察图形可知，可判断D.【详解】由已知得圆的圆心，半径，圆的圆心，半径，因为，，故两圆相交，所以与的公切线恰有2条，故A错误；两圆方程做差可得与相交弦的方程为，故B正确；由点到直线的距离公式得到相交弦的距离为，故相交弦的弦长为，C正确；.由图可知，，故D正确.故选：BCD【变式43】（20222023·山东烟台·高二上·期中）（多选）圆与圆相交于，两点，则（）A.的直线方程为 B.公共弦的长为C.圆与圆的公切线长为 D.线段的中垂线方程为【答案】ACD【解析】【分析】对于A，两圆方程相减可求出直线的方程，对于B，利用弦心距、弦和半径的关系可求公共弦的长，对于C，求出，再由可求得结果，对于D，线段的中垂线就是直线，求出直线的方程即可.【详解】由，得，则，半径，由，得，则，半径，对于A，公共弦所在的直线方程为，即，所以A正确，对于B，到直线的距离，所以公共弦的长为，所以B错误，对于C，因为，，，所以圆与圆的公切线长为，所以C正确，对于D，根据题意可知线段的中垂线就是直线，因为，所以直线为，即，所以D正确，故选：ACD【变式44】